
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:42.
- Senast ändrad 2025-01-23 15:11.
Av arrowlikeFölj mer av författaren:


I klassrummet använder vi ofta ett stoppur för att genomföra pendelförsöket eller ett enkelt harmoniskt rörelseexperiment. Här är en utmaning, kan vi ta fram en riktig graf över dess rörelse och se vad som är den momentana vinkelpositionen och hastigheten, det är mycket mer information och roligt.
Första frågan, vi måste bestämma att pendelkroppen är en viktlös sladd eller en styv enhetlig stav. Sladdstrategin verkar vara enklare. Från praxis att bygga en har jag följande avvägningar: Det enklaste sättet att hänga ett pendelsystem kan vara att hänga det på dörrens övre kant. Det ger din ~ 2 m pendellängd utan att göra några strukturella byggnadsarbeten. Men den behöver inte att gungan inte kommer att röra vid dörrytan, vilket helt enkelt förstör hela experimentet. Så planet det ska svänga ska vara exakt parallellt med din vägg/dörryta. En viktlös sladd tenderar att vara tunn, den kan snurra lätt och komplicera mätningen av svängningsvinkel. Vi vill använda en mätning för att representera svängningstillståndet. Tunn sladd, till exempel fisklinje, kan vara elastisk och töjbar, vilket påverkar en av våra viktigaste konstanter som mäts av oss och används i ekvationen, vilket är pendelns längd. Vissa kan också påverkas av temperaturen. Viktmängden som hänger i änden av sladden måste vara tillräckligt tung så att vikten av sladden blir försumbar. Kommentera gärna om du håller med eller inte håller med dem, eller om du har andra idéer om designavvägningar. För att studera detta problem behöver vi en enhet som är så lätt att dess vikt kan ignoreras och vi behandlar fortfarande pendelsystemet som en stel enhetlig stav. Jag använder en COTS -bärbar elektronisk styrenhet, som levererar gyro-, accelerometer- och vinkelinformation till oss via Bluetooth -anslutning. Dessa mätningar lagras i en datafil för en mobiltelefonapp. Därefter analyserar vi data för vårt enkla harmoniska rörelseexperiment. Den numeriska analysen fokuserar på följande ämnen: 1) Förutse pendeloscillationsperioden 2) Samla programmerbart in pendeln enkla harmoniska rörelseexperimentdata 3) Använd kmean för att gruppera data och ta bort outliers i analysprocessen 4) Använd korttids-FFT för att uppskatta pendelns oscillationsfrekvens
Tillbehör
Bluetooth -mätapparat
Android -telefonapp: Gå till Google playstore, sök i M2ROBOTS och installera kontrollappen. Om det är svårt att komma åt Google playstore, besök min personliga hemsida för alternativ appnedladdningsmetod
trästav
några 3D -tryckta delar
sågblad eller liknande metallmaterial
Steg 1: Vad är pendel? Hur modellerar man det?
Det finns många artiklar och böcker som introducerar pendelekvationsderivationen, inklusive din läroplanens fysikbok. Sådant innehåll kan vara bättre att inte upprepas här igen. Endast den slutgiltiga slutsatsen listas här angående ämnet "enkel harmonisk rörelse". För att kunna veta en pendels period är allt vi behöver veta pendelns längd, betecknad som "l", i meter.
Om vi är ganska säkra på att vikten ligger nästan helt i slutet av en viktlös sladd som hänger i en sväng och pendeln svänger i små vinklar θ, säg mindre än 15 °, ges perioden T1 för en sådan pendel av:
T1 = 2*pi*(l/g)^0,5
g = tyngdacceleration, ungefär 9,8 m/s^2
Om den viktlösa sladden ersätts av en stel enhetlig stav, återigen med längden l, ges dess enkla harmoniska rörelseperiod T2 med T1 = 2*pi*(2l/3g)^0,5
Effektivt har den samma period som en viktlös sladdpendel som är två tredjedelar av den styva enhetliga stavlängden.
Detta är bakgrunden, och vi kan börja förbereda vårt experiment.
Steg 2: Förbered delarna för hårdvarubyggnad



För att bygga pendelstrukturen, 3D -printar vi några delar och återvinner något vi redan har. Den övergripande pendelstrukturen visas i figur 1. Det är en blandning av 3D -printdelar tillsammans med några handgjorda delar och en lång bit trästav från Lowes.
Den 3D -tryckta delen i figur 2 hänger på en dörrs överkant, eftersom vår dörr är en lätt plan yta för oss att hänga något. STL -nedladdningslänk:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Den gröna delen i figur 3 ansluter trästången till ett blad, och bladet sitter ovanpå två skenbitar monterade på den tidigare 3D -tryckta dörrhängaren. STL -nedladdningslänk:
De två skenbitarna är gjorda genom att bryta ett gammalt sågblad på mitten, se fig. 4. Delen i figur 2 har förberett rätt slitsstorlek för dem. Helst kan vi göra ett "V" -format hack i de två sågklingorna med hjälp av en fil. En någorlunda vass kantad metall, som ett rakblad med en kant, eller någon handgjord metallbit, kan sitta inuti de "V" -formade skårorna. Anledningen till att vi behöver en mindre kontaktyta är att minska den rörelseenergi som går förlorad när den svänger.
Den sista 3D -tryckta delen i figur 5 är ett litet fack för den elektroniska mätapparaten.
Nedladdningslänken:
Bluetooth -mätapparaten genererar vinkeluppskattning, gyromätning och accelerometermätning. All denna data är tillgänglig för oss via trådlös Bluetooth -länk.
Vi kommer att genomföra flera experiment genom att distribuera denna apparat vid olika position för pendelarmen och se skillnaderna.
Steg 3: Experimentdatainsamling



Det finns två genomförbara metoder för experimentell datainsamling innan vi analyserar den förvärvade datamängden:
1) Använd Android -telefonappen som anges i kravavsnittet för att logga in alla mätningar som produceras av apparaten i en datafil som är lagrad på telefonens SD -kort. Vi kan kopiera filen och efterbehandla informationen.
2) Använd en Bluetooth-aktiverad dator, en PC, en bärbar dator eller en RaspberryPi-minidator för att upprätta en Bluetooth-anslutning till apparaten och läsa data för antingen realtids- eller offline-analys.
Det finns både fördelar och nackdelar för varje metod, vi kommer att prova båda och berätta skillnaden i denna instruerbara.
För metod (1) med Android -appen, när vi väl är i Android App -gränssnittet, kommer telemetradata som skickas från Bluetooth -mätapparaten till Android -telefonen att spelas in i en datalogfil med namnet m2flightDatayyyymmdd_hhmmss.txt. Den finns i din Android -telefons nedladdnings-/m2LogFiles -mapp. Mappen "Ladda ner" är en befintlig mapp i telefonens Android OS och "m2LogFiles" är en mapp som appen skapade. Filnamnets innehåll yyyymmdd_hhmmss är sättet att koda experimentets starttid (år, månad, dag, timme, minut och sek) i filnamnet.
Varje rad i loggfilen är en post. Det börjar med händelsens tidsstämpel, inledningssträngen "eam:", följt av 4 triplettdata, som är:
Accelerometer XYZ -axelavläsning i rå sensorhårdvararegistreringsvärden
Gyroskop XYZ -axelavläsning i rå sensorhårdvara registrerar återläsningsvärden
Magnetometer XYZ -axelavläsning i rå sensorhårdvara registrerar återläsningsvärden
ombord beräknad Roll/Pitch/Raw i grad
Datafilen som skapas med datorns pythonprogram använder identiska datafilformat, så att programmet vi använder i dataanalyssteget inte störs av datakällan som produceras av vårt pythonprogram eller Android -appen.
Låt oss börja koda med metod (2).
För att interagera med Bluetooth -mätapparaten tillhandahålls två smaker av SDK:
1) Python SDK, som kan installeras med "pip3 install m2controller", python3 är språket som används. Exemplen på användarkodskod lagras i https://github.com/xiapeiqing/m2robots/tree/maste… För detta experiment kommer vi att använda python script pendulum1.py
2) Java SDK, som inte används i denna instruerbara eftersom vi vill ha senare visualisering och analys av de förvärvade pendeldata, vilket kan ta lite mer ansträngning för oss att programmera i Java.
Programkällkoden för python3 -datainsamlingsprogrammet innehåller många kommentarer för kodfunktionens detaljer. En ögonblicksbild av källkoden finns här.
#!/usr/bin/env python#-*-kodning: UTF-8-*-från m2controller import m2controller från m2controller import m2Const import signal import tid import datetime import usrCfg import pendel2
requestExit = Falskt
################################################################
#vi vill använda samma loggfilnamnkonvention så att dataanalysmodulen, pendulum2.py, kan vara agnostisk för hur vi får loggdatafilen ################# ################################################# logfilename = " m2flightData%s.txt "%(datetime.datetime.fromtimestamp (time.time ()). strftime ('%Y%m%d_%H%M%S')) dataLogfile = open (logfilnamn," w ")
def signal_handler (sig, frame):
global requestExit-utskrift ('användare Ctrl-C för att avsluta programkörning') requestExit = True signal.signal (signal. SIGINT, signal_handler)
################################################################
#när varje mätdata blir tillgänglig med 20Hz -hastighet kommer denna "återuppringnings" -funktion att kallas ################################ ################################## def callbackfunc (telemetri): strTimeStamp = datetime.datetime.fromtimestamp (time.time ()). strftime ('%H:%M:%S.%f') [:-3] dataStr = "%s, eam:%d,%d,%d,%d,%d,%d, %d, %d, %d, %2.1f, %2.1f, %2.1f / n " %(strTimeStamp, telemetri ['m_fAccelHwUnit'] [0], telemetri ['m_fAccelHwUnit'] [1], telemetri ['m_fAccelHwUnit'] [2], telemetri ['m_fGyroHwUnit'] [0], telemetri ['m_fGyroHwUnit'] [1], telemetri ['m_fGyroHwUnit'] [2], telemetri ['m_fMagHwUnit'] ['m_fMagHwUnit'] [1], telemetri ['m_fMagHwUnit'] [2], telemetri ['m_fRPYdeg'] [0], telemetri ['m_fRPYdeg'] [1], telemetri ['m_fRPYdeg'] [2]) ## #################################################### ##############vi skriver ut datasträngen till skärmen och sparar dem i loggfilen ####################### ########################################### print (dataStr) dataLogfile.writelines (dataStr)
################################################################
#initiera styrenheten, kom ihåg att ställa in fältet BleMACaddress som enhetens MAC -adress ################################## #################################TODO: låt oss initialisera BleMACaddress om den inte ställs in av användaren. controller = m2controller. BleCtrller (m2Const.etDebian, callbackfunc, usrCfg. BleMACaddress) controller.connect () medan True: ########################### ########################################vänta på att mätdata skapas och skickas från pendelmätningen apparat ################################################### ################ controller.m_CommsTunnel.waitForNotifications (1.0) if requestExit: ######################### ##########################################hushållning fungerar här när vi avslutar dataloggning #################################################### ############### controller.stop () dataLogfile.close () break
################################################################
#datainsamling slutförd, låt oss nu analysera loggdata ######################################### ########################## pendulum2.parseDataLogFile (logfilnamn)
För långsiktig uppdatering, kolla in
Låt oss nu förklara dess driftsmetod. Detta python -program är skrivet ovanpå ett pip -installerbart paket, som heter m2controller. Paketet på lägre nivå erbjuder återuppringningsmekanism, så att varje mottagen mätuppdatering utlöser den återuppringningsfunktion som vi skrev och sparar data i en lokal loggfil. Formatet för loggfilens datainnehåll är identiskt med det som produceras av Android -följeslagarappen, så att dataloggfilen som skapats av antingen pythonprogram eller andriod -följeslagarapp är utbytbar.
Användarens ctrl-C-signal, som fångas upp av operativsystemet, skickas till programmet och stoppar den oändliga slingan som väntar på att nya mätdata kommer.
Hittills har loggfilen skapats framgångsrikt, och detta program kommer att kalla analysprogrammet för att studera våra experimentresultat.
Här är två experiment, och jämförelsen visar den mycket märkbara skillnaden genom att fästa en 7 gram enhet på olika platser.
I figur 2 använder vi en skala för att bestämma den faktiska vikten för denna bluetooth -mätapparat.
Fig. 3 visar pendelinställningen där 7gram -enheten är fäst vid pendelns nedre ände. Inställningskonfigurationen i fig. 4 har en massa på 7 gram som ligger mycket närmare den svängande pivot.
Fig. 5 är en närbild av pendelstrukturen.
Steg 4: Dataanalys



Bluetooth -mätapparaten väger ~ 7 gram, vilket väger mycket mindre än en ~ 1,6 meter lång träpinne. Använd antagandet om "stel enhetlig stav", så har vi denna pendelperiodekvation, T1 = 2*pi*(2l/3g)^0,5
För att få gravitationskonstanten kan vi använda 9,8 m/s^2. Men en mer exakt gravitationskonstant vid en given geolokalisering kan hämtas från denna webbtjänst:
www.wolframalpha.com/widgets/view.jsp?id=e…
För san francisco är det 9,81278m/s^2
Pendellängden mäts till 64,5 ''
2*pi*sqrt (2*64,5*0,0254/(3*9,81278)) ger den förväntade pendeltiden 2,0962 (sek).
Låt oss se om det stämmer överens med våra experiment.
I det första experimentet har pendelinstallationen 7gram -enheten ansluten till pendelns nedre ände. Min loggfil kan laddas ner i:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Byt namn till "PendulumTestData.txt" och lägg den i samma mapp i pythonanalysprogrammet. En ögonblicksbild av källkoden finns här.
#!/usr/bin/env python#-*-kodning: UTF-8-*-import csv import matplotlib.pyplot som plt plt.style.use ('seaborn-whitegrid') import numpy som np från datetime import datetime, timedelta import seaborn som sns från sklearn.cluster import KMeans från samlingar importräknare ################################### ###############################denna funktion kör datafilanalysarbetet ############# #################################################### ## def parseDataLogFile (datafilename): ########################################### ########################extrahera data i den kommaseparerade dataloggfilen (CSV) och spara innehållet i varje kolumn i en variabel av float-typ ## #################################################### ############# med öppet (datafilename) som csvfile: readCSV = csv.reader (csvfile, delimiter = ',') timestampS = fAccelHwUnit_x = fAccelHwUnit_y = fAccelHwUnit_z = fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUni t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = för rad i readCSV: försök: x = datetime.strptime (rad [0].split (',') [0], '%H:%M:%S.%f ') timestampS.append (timedelta (timmar = x.timme, minuter = x.minut, sekunder = x.sekund, mikrosekunder = x.mikrosekund).total_seconds ()) fAccelHwUnit_x.append (float (rad) [1] [4:])) fAccelHwUnit_y.append (float (rad [2])) fAccelHwUnit_z.append (float (rad [3])) fGyroHwUnit_x.append (float (rad [4])) fGyroHwUnit_y.append (float (rad [5])) fGyroHwUnit_z.append (float (rad [6])) fMagHwUnit_x.append (float (rad [7])) fMagHwUnit_y.append (float (rad [8])) fMagHwUnit_z.append (float (rad) [9])) fRPYdeg_r.append (float (rad [10])) fRPYdeg_p.append (float (rad [11])) fRPYdeg_y.append (float (rad [12])) utom: passera tidsstämpelS = np.asarray (tidsstämplar) tidsstämplar = tidsstämplar - tidsstämplar [0] fAccelHwUnit_x = np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np.mean (fRPYdeg_p) fRPYdeg_y = np.asarray (fRPYdeg_y)
################################################################
#vi behöver exakt uppskattning av samplingsfrekvensen för exakt uppskattning av oscillationsperioden ##################################### ############################# FsHz = getSamplingIntervalS (tidsstämplar) ################# ################################################ # använda sig av tonhöjdskomponent i inställningshuvudreferenssystemutgång för pendelperiodanalys ####################################### ############################ analys_timeSequence (tidsstämplar, fRPYdeg_p, FsHz, "tonhöjd") ########### #################################################### ####använd acceleromter råmätning för pendelperiodanalys ###################################### ############################ analys_timeSequence (tidsstämplar, fAccelHwUnit_x, FsHz, 'accel') ############ #################################################### ####använd gyro råmätning för pendelperiodanalys ###################################### ############################ analys_timeSequence (tidsstämplar, fGyroHwUnit_y, FsHz, ' gyro ') print (' klart, grattis:-) ') plt.show () ################################# ###################################i Bluetooth -kommunikationsprocessen, det finns en sällsynt chans att datakommipaketet kan gå förlorad#vi använder K-medel för att isolera 20Hz mätdata från outliers, som orsakas av tappat paket#dyk i "signal och system för mer information" ################ ################################################## def getSamplingIntervalS (tidsstämpel): plt.figure () sampleIntervalS = np.diff (timestampS) sns.distplot (sampleIntervalS) plt.ylabel ('histogram') plt.xlabel ('mätintervall (er)') clusterCnt = 5 km = KMeans (n_clusters = clusterCnt) km.fit (sampleIntervalS.reshape (-1, 1)) centroids = km.cluster_centers_ elemCnt = Counter (km.labels_) occurrenceCnt = for ii in range (clusterCnt): occurrenceCnt.append (elemCnt [ii]) FsHz = 1/centroids [förekomstCnt.index (max (förekomstCnt))] retur FsHz
################################################################
#använd spektrometer, dvs kort tid FFT för att få frekvenskomponenten, toppbehållaren är vår bästa uppskattning av pendeloscillationen ########################### ###################################### def analys_timeSequence (tidsstämplar, timeSeqData, FsHz, strComment): fig, (ax1, ax2) = plt.subplots (nrows = 2) ax1.plot (timestampS, timeSeqData, marker = 'o', markerfacecolor = 'blue', markersize = 2, color = 'skyblue', linewidth = 1) ax1.set_title ("mätning av pendeltidsdomän - %s" %strComment) ax1.set_xlabel ("provtagningstid (andra)") ax1.set_ylabel (strComment); NFFT = 2048 # längden på fönstersegmenten
Pxx, freqs, bins, im = ax2.specgram (timeSeqData, NFFT = NFFT, Fs = FsHz, noverlap = NFFT/2)
ax2.set_title ("Spectrogram") ax2.set_xlabel ("samples") ax2.set_ylabel ("frekvens (Hz)");
# Metoden `specgram` returnerar 4 objekt. Dom är:
# - Pxx: periodogrammet # - frekvenser: frekvensvektorn # - fack: tidsfackens centrum # - im: matplotlib.image. AxesImage -instansen som representerar data i tomten pkresult = np.where (Pxx == np.amax (Pxx)) oscFreqHz = freqs [pkresult [0] [0] print ('pendeloscillation Freq (Hz) =%f, Period (Sec) =%f, uppskattningsdatakälla:%s'%(oscFreqHz, 1/oscFreqHz, strComment)) returnera 1/oscFreqHz
################################################################
#ska vi köra detta program oberoende, det vill säga, inte kallas av pendulum1.py,#definierar vi ett standardloggdatafilnamn som ska analyseras ##################### ############################################## om _name_ == "_ huvud_ ": defaultFilename = './PendulumTestData.txt' import os.path if os.path.isfile (defaultFilename): parseDataLogFile (defaultFilename) else: print (" standard loggfil %s finns inte " %defaultFilename)
För långsiktig uppdatering, kolla in
Källkoden innehåller detaljerade kommentarer, låt oss ge en hög sammanfattning av den matematiska uppskattningen här.
1) Vi läste först in CSV -filinnehållet i datorn med ett python -paket som heter "csv". Vi har periodiska mätningar.
21: 34: 26.362, eam: 0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0.5, -5.5, 40.5
21: 34: 26.373, eam: 128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0.5, -6.5, 40.0
21: 34: 26.412, eam: 448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0.5, -7.5, 40.5
21: 34: 26.462, eam: 448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0.5, -8.0, 40.5
2) Eftersom mäthastigheten är så kritisk och direkt introducerar beräkningsfel i pendelperioden, vill vi uppskatta dem. Vårt nominella mätintervall är 50 ms, dvs 20Hz. Genomsnitt över alla mätningar verkar OK, men vi förlorar ibland paket med dataöverföring, uppdateringsintervallet blir 100 ms eller 150 ms, …
Om vi plottar förekomsten av dessa data, se figur 1, som en människa, kan vi enkelt ha ett ögonbollvärde på 0,05 sekunder. Men kan vi göra bättre än så?
Vi behöver använda klassificeringsmetoden för att bara välja de bra för medelvärdesberäkning. Python har verktygslådan som heter KMeans för att hjälpa oss med klustering, eller säg klassificering. Dessa begrepp används i många stora data- och AI -områden.
3) Bild 2 innehåller två bilder. Det översta diagrammet är en tidsdomän-sekvens för vår svängande vinkelmätning i grader. Genom att hänvisa till x-axelns tidsstämpel i andra kan vi läsa cirka 22,5 cykler på 50 sekunder, vilket innebär 2,22 sek pendelperiod. Finns det ett sätt att automatisera denna process och få en mer exakt uppskattning? Ja, vi kan använda ett matematiskt verktyg som kallas spektrogram, som använder en liten bit mätdata och berättar dess frekvens, se figuren nedan. Y-axelavläsningen för den mörkaste linjen är pendeloscillationsfrekvensen. Att vara en horisontell linje bekräftar att pendeloscillationen inte förändrades alls under hela experimentet. Det inversa värdet av oscillationsfrekvensen är pendeloscillationsperioden.
Slutrapporten från programmet är en textöversikt:
pendeloscillationsfrekvens (Hz) = 0.449224, period (sek) = 2.226059, uppskattningsdatakälla: tonhöjd
Vi kan hitta vårt tidigare ögonblickande handberäkningsresultat, 2,22 sekunder, är ganska förenligt med programmets beräknade värde.
Jämfört med 2.0962 (sek) teoretiskt beräknat värde har vi ~ 5% återstående fel. Hur bli av med dem? Kom ihåg att antagandet är "stel enhetlig stav"? Även en 7 gram extra vikt verkar trivial, det är den största orsaken till det återstående felet.
Vi flyttar nu enheten, nära pivot. Se föregående steg för en närbild. Loggfilen jag skapade kan laddas ner här:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Kör samma analyssteg, så får vi Perioden 2.089867 (sek), se figur 3, som är nästan identisk med den teoretiska förutsägelsen. Bra!
Eftersom vi inte bara har svängande vinkelmätning, utan också gyroskopisk mätning och accelerometermätning i samma takt. Kör samma analys för de andra två mätningarna, vi får resultat i figur 4 och 5. Uppskattningar från alla tre mätkällorna är överens, vilket gör oss mer säkra på framgången med vårt experiment.
Här är resultatet som den slutliga utmatningen av pythonprogram som körs:
pendeloscillationsfrekvens (Hz) = 0.478499, period (sek) = 2.089867, uppskattningsdatakälla: tonhöjd
pendelsvängningsfrekvens (Hz) = 0.478499, period (sek) = 2.089867, uppskattningsdatakälla: accel
pendeloscillationsfrekvens (Hz) = 0,478499, period (sek) = 2,089867, uppskattningsdatakälla: gyro
Senaste tanken i detta steg, hur kan uppskattningsresultaten vara exakt identiska med olika ingångskällor? Detta är motintuition. Jag lämnar denna fråga till läsarna. Här är en ledtråd: kom ihåg att vi använder korttids-FFT för att uppskatta oscillationsfrekvensen? I digital domän ges frekvensuppskattningen i diskreta frekvensfack istället för en uppskattning av flytande antal.
Steg 5: Framtidsarbetsrekommendationer
Det finns få kategorier av framtida arbetsrekommendationer.
I tidigare steg lyckas vi minska vårt experimentfel från ~ 5% till mindre än 1%, kan vi göra det bättre än så? Att märka oscillationsstorleken minskar exponentiellt, en bidragande faktor kan vara luftdraget som orsakas när pendeln svängs. Pendelns tvärsnitt kan behöva modifieras för att ha en strömlinjeformad form för att minska det aerodynamiska motståndet.
Kan vi tillämpa en tidsvarierande förstärkning som lärt sig med adaptiva filtertekniker för att mata ut en konstant toppstorlekssignal. Under tiden, korrelera storleksdämpningen kommer externa krafter.
Vi kan knappt hitta något enklare än den "enkla harmoniska rörelsen". Kan vi använda de anläggningar vi analyserar pendeln för att analysera något mer komplicerat, en sportaktivitet, en vattenraketuppskjutningssekvens osv?
Glad hackning
Rekommenderad:
Ljudsensor och servo: reaktiv rörelse: 4 steg

Ljudsensor och servo: reaktiv rörelse: Först måste du samla relevant material för att sätta ihop denna krets
RGB-ljusdriven rörelse i handflatorna Kontaktlös: 4 steg

RGB-ljusdriven rörelse i handflatorna Kontaktlös: RGB-nattljus, med möjlighet att styra nattljusets färg med hjälp av handrörelser. Med hjälp av tre avståndssensorer ändrar vi ljusstyrkan för var och en av de tre komponenterna i RGB -färgen när du närmar dig eller tar bort handen. Ett ar
Enkel gestkontroll - Styr dina RC -leksaker med armens rörelse: 4 steg (med bilder)

Enkel gestkontroll - Styr dina RC -leksaker med armens rörelse: Välkommen till min "ible" #45. För ett tag sedan gjorde jag en fullt fungerande RC-version av BB8 med Lego Star Wars-delar … https://www.instructables.com/id/Whats-Inside-My-R…När jag såg hur coolt det var Force Band gjord av Sphero, tänkte jag: " Ok, jag kan
Potentiometer och servo: kontrollerad rörelse med Arduino: 4 steg
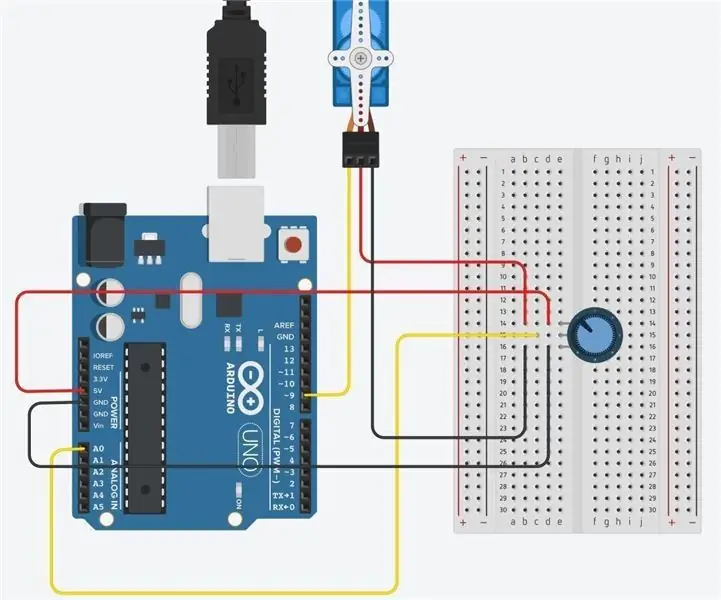
Potentiometer och servo: kontrollerad rörelse med Arduino: Först måste du samla relevant material för att sätta ihop denna krets
2 potentiometrar och 2 servon: kontrollerad rörelse med Arduino: 4 steg
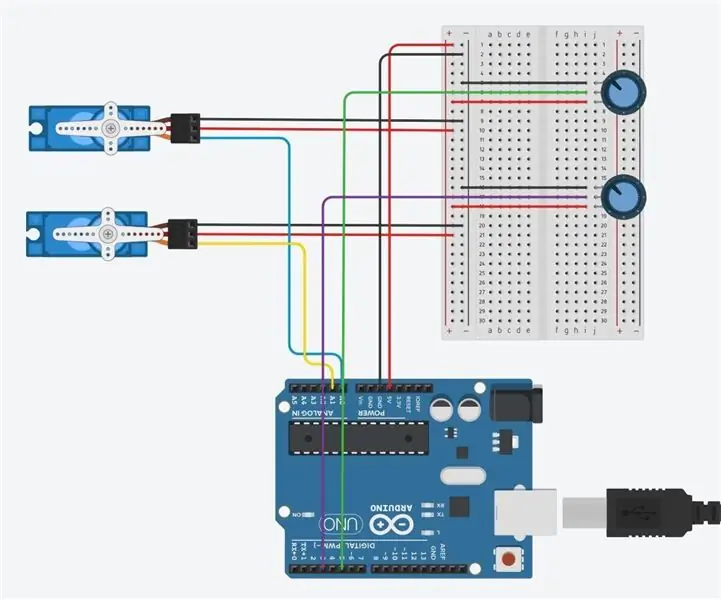
2 potentiometrar och 2 servon: kontrollerad rörelse med Arduino: Först måste du samla relevant material för att sätta ihop denna krets
