Rekursivt summering av en matris i Java: 9 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:40

Rekursion är en mycket användbar och tidseffektiv procedur som snabbt kan lösa ett problem med mycket liten kod. Rekursion innebär den metod du skapar som kallar sig förkorta det ursprungliga problemet.

I det här exemplet summerar vi en array med 10 heltal, men storleken kan vara av vilken längd som helst.

Tillbehör

Du bör känna till grundläggande java -syntax och ha din IDE eller en textredigerare för att skriva din kod för denna uppgift.

Steg 1: Konfigurera din huvudmetod

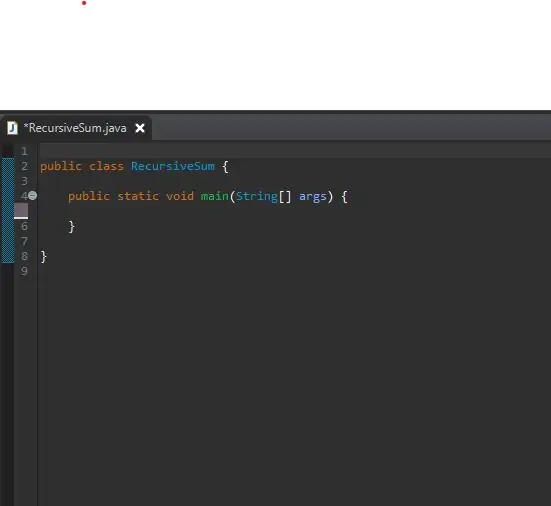
Börja med att konfigurera din huvudmetod i en nyskapad klass. Jag har döpt min klass till RecursiveSum. Det är här du kommer att skapa en rad heltal och ringa din rekursiva metod.

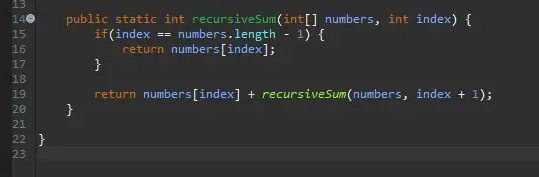
Steg 2: Skapa din rekursiva metodrubrik

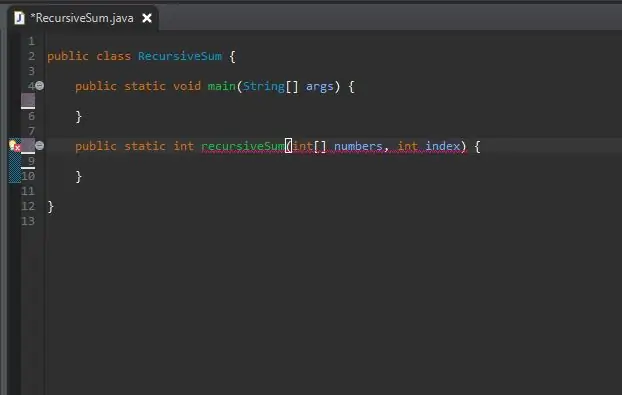
Utanför din huvudmetod, skapa metodhuvudet för din rekursiva metod.

Metoden är statisk, eftersom den inte kommer att kräva att ett objekt används på den.

Returtypen är int, eftersom matrisen vi kommer att använda kommer att vara full på heltal. Detta kan dock ändras till vilken nummertyp som arrayen innehåller.

Jag har namngett min metod recursiveSum som tar två parametrar; en rad heltal och index som vi kommer att lägga till summan. Jag har kallat dessa parametrar för nummer respektive index.

Du kommer att se fel just nu och det är bra. De kommer att åtgärdas senare.

Steg 3: Skapa ditt Kicker/basfodral

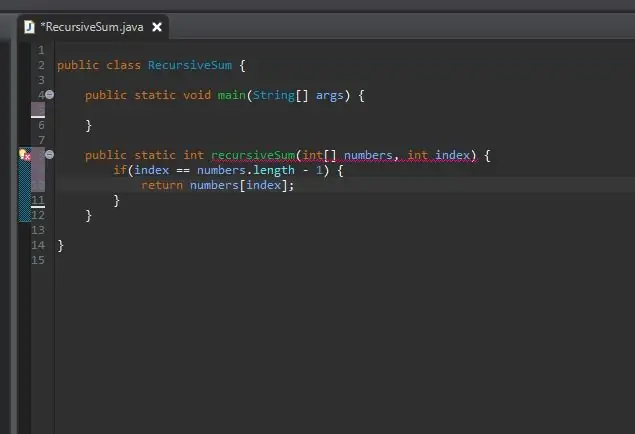
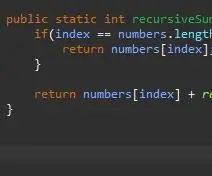
En rekursiv metod kräver ett kicker/basfall. Detta är villkoret som kommer att stoppa din metod från att oändligt kalla sig själv. Detta basfall kan ses som det enklaste fallet vi kommer att stöta på. I det här fallet är basfallet när vi är i slutet av vår array. Om det aktuella indexet är lika med matrisens längd (minus 1 eftersom matriser börjar räkna från 0 inte 1), är vi i slutet och vi returnerar bara det elementet vid det indexet.

Steg 4: Det rekursiva steget

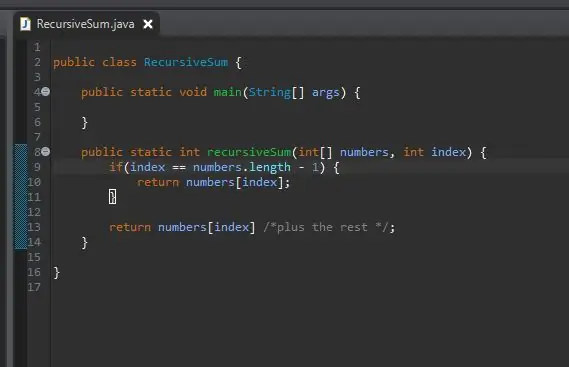
När vi väl har vårt basfall är nästa steg vårt rekursiva steg. Det är här magin händer. Vi har hanterat fallet när vårt index är det sista elementet i vår array. Vad händer om vi inte är det sista elementet i vår array? Vad händer om vi helt enkelt kunde säga det att lägga till vårt nuvarande element plus nästa? Så småningom kommer vi att träffa slutet av vår array och vårt basfall kommer att påverka.

För att åstadkomma detta returnerar vi helt enkelt vårt nuvarande index och "lägg till resten" av matrisen.

Steg 5: Förkorta problemet

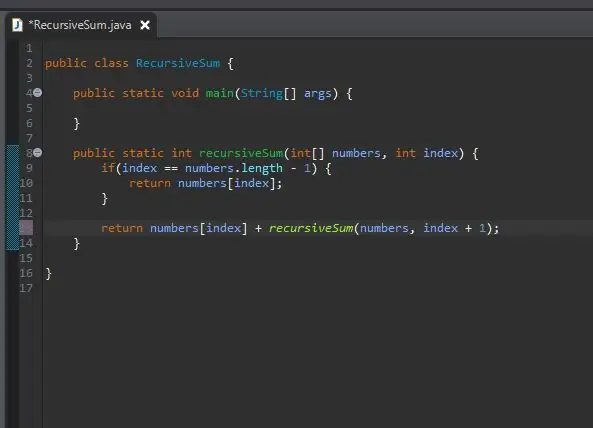
Hur kan vi helt enkelt "lägga till resten"? Vi har redan en metod som kommer att lägga till ett visst element; vår rekursiveSum () -metod! Vi kan kalla det igen men ändra vilket index vi summerar.

Vi passerar i samma array som vi bearbetar, men vi skickar in nästa index från vårt nuvarande index. Vi gör detta genom att helt enkelt lägga till ett till vårt nuvarande index som visas.

Steg 6: Skapa matrisen av heltal

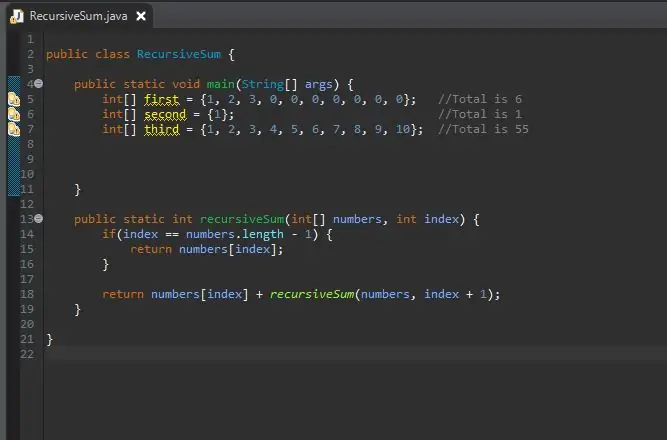
Nu när vår rekursiva summeringsmetod är klar kan vi skapa vår array som vi kommer att bearbeta. Denna matris kommer att finnas i vårt huvudmetodblock.

Du kan göra storleken på matrisen så länge du vill. Jag har skapat några olika matriser med olika storlekar och värden för att visa att det fungerar inte bara på en enda storlek.

Steg 7: Ring metoden med dina matriser

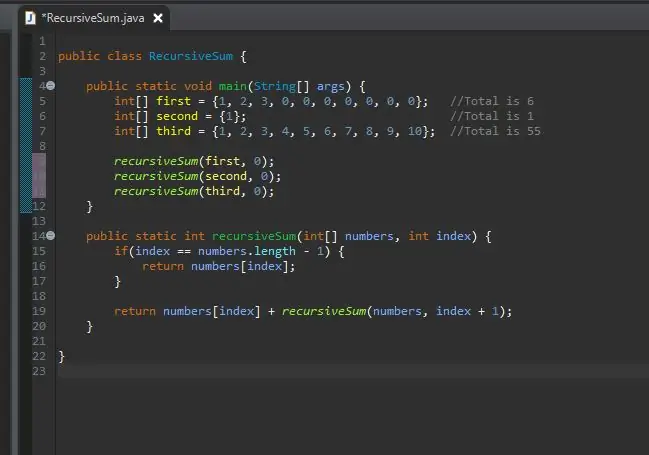
Nu kan du ringa din rekursiva metod och skicka dessa matriser till den. Nu kan du köra ditt program.

Steg 8: Skriv ut resultaten

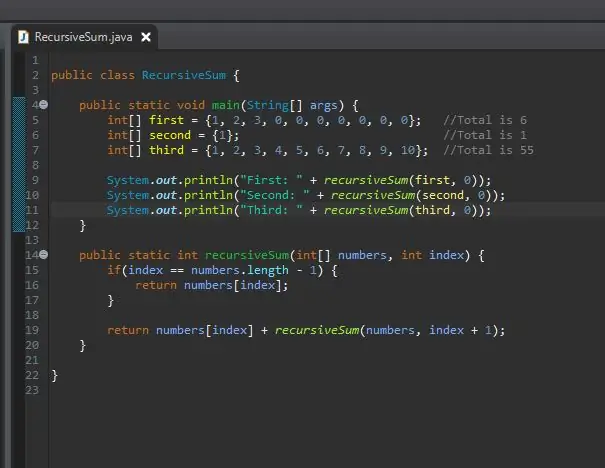
Inget hände. Varför? Rekursiv summa returnerar ett heltal men vi har inte gjort något med detta heltal. Det gjorde sitt jobb men vi kan inte se resultatet. För att se resultatet, skriver vi ut det helt enkelt. Efter att ha kört detta bör du se resultaten för var och en av dina matriser.

Steg 9: Grattis

Du har slutfört en rekursiv funktion. Ändra gärna storleken på dina matriser. Om du testar det märker du att det kraschar när du har en tom matris. Vi har inte redogjort för det, men det är ett bra sätt att förbättra din rekursiva metod.