Ögonklippning Din ögonbolls recept: ett BME60B -projekt: 9 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:37

Av: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Förstoring är en av de viktigaste funktionerna som finns för läsglasögon, som klassificeras efter deras recept på dioptrar. Enligt Michigan Technology University är en dioptri en objektivets brännvidd, vanligtvis mätt i mm, i mätenheten (Michigan Technology University). Eftersom läsglasögon har konvexa linser skulle brännvidden vara positiv och orsaka att dioptrarna också är positiva (HyperPhysics). Brännvidden ökar när avståndet mellan objektet kommer längre bort från det faktiska objektivet, och detta leder till att dioptrarna minskar eftersom de är omvänt proportionella. Därför skulle läsglasögon med ytterligare dioptrier hjälpa linsen att zooma in i vyn så att det kan tyckas att brännvidden är mindre genom att öka värdet på dioptrarna.

Koden som presenteras kommer att användas för att förutsäga dioptri hos ett objektiv med ett okänt recept. Två ingångar används för att beräkna receptet: ett fotografi av den kontrollerade bakgrunden utan att använda några linser, och ett annat fotografi med samma bakgrund men genom det valda objektivet. Programmet mäter snedvridningen mellan dessa två fotografier. Därifrån kommer vi att kunna uppskatta linsens dioptri och producera ett resultat som användaren kan se.

För denna instruktör behöver du:

• Ett svart-vitt rutmönster tryckt på ett 11x8,5 i pappersark
• En kamera med möjlighet att låsa fokus
• Ett stativ, eller något liknande för att säkra kameran
• Olika recept på läsglasögon
• MATLAB

Steg 1: Ta foton

För att beräkna förstoringen av ett objektiv måste du kunna jämföra det med objektets faktiska storlek. För detta projekt kommer vi att jämföra en förstorad bild med en kontrollbild.

Således är det första steget att ta två bilder av samma bild - den första genom bara kameran och den andra genom objektivet på läsglasögonen du vill testa.

Du kommer att ta en bild av en 8.5x11in svart och vit schack med ett 1in rutnät. Ställ din kamera 11in bort från schackbrädet. Innan du tar bilderna låser du fokus på rutan.

Ta ett foto av rutan utan läsglasögonen. Placera sedan läsglasögonen framför kameran utan att flytta något och ta det andra fotot.

Se till att kamerans position inte rör sig mellan bilderna. Det enda som bör förändras mellan de två fotona är närvaron av glasögonlinsen framför kameran.

När du är klar med bilderna laddar du upp dem till din dator.

Steg 2: Ladda in bilderna i MATLAB

Öppna ett nytt skript.

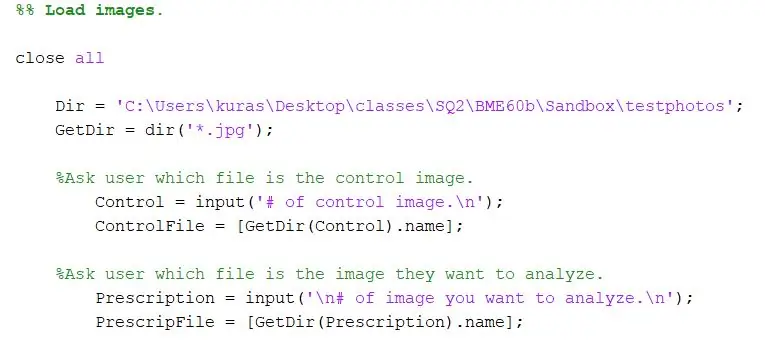
Ange först katalogen där fotona lagras. Använd sedan dir -funktionen för att extrahera-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

För vårt projekt ville vi uppmana användaren av programmet för vilka filer de ville jämföra. Det första avsnittet uppmanar användaren att ange kontrollbilden och det andra ber användaren att ange testbilden.

• %Fråga användaren vilken fil som är kontrollbilden.
• Control = input ('# of control image. / N');
• ControlFile = [GetDir (Control).name]
• %Fråga användaren vilken fil som är bilden de vill analysera.
• ChooseFile = input ('\ n# av bilden du vill analysera. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Steg 3: Bildanalys

En färgad bild i MATLAB är av storlek MxNx3, medan en gråskala bild är MxN. Det betyder att det är snabbare att förbättra/redigera en gråskala bild eftersom det finns mindre data att hålla reda på. Använd rgb2gray för att konvertera bilden till gråskala. (Imrotatfunktionen användes eftersom våra foton kom horisontellt - den här kodraden kan vara nödvändig i din version.)

• %konvertera till gråskala och rotera
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotate (I, 90);

Visa sedan bilden. Delplotfunktionen används för att testbilden ska kunna ligga bredvid kontrollen i senare steg.

• %visa
• Figur 1);
• delplan (1, 2, 1)
• imshow (I);
• titel (ControlFile);

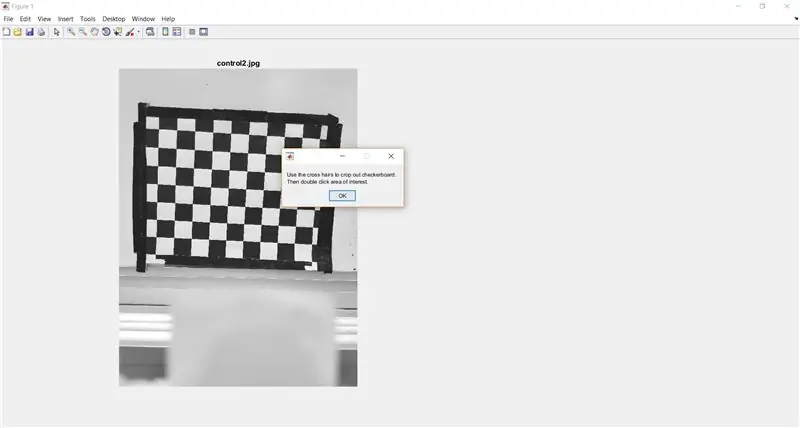
Använd imcrop för att uppmana användaren att beskära rutan ur hela bilden. Följande kod visar också en meddelanderuta som ger användaren instruktioner.

• %beskära rutan för analys
• waitfor (msgbox ({'Använd korthåren för att beskära rutan.', 'Dubbelklicka sedan på intresseområdet.'}));
• I_crop = imcrop (I);

Använd imbinarize för att binarisera bilden.

I_binary = imbinarize (I_crop);

Steg 4: Beräkna bredden på de vita rutorna på rutan

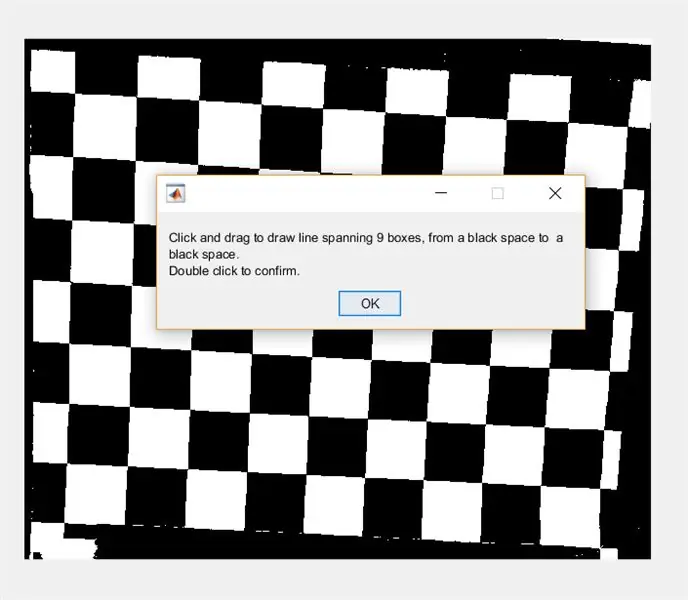
Uppmana sedan användaren att dra en linje över bilden med hjälp av imline. Denna linje ska löpa horisontellt över schackbrädet. Det bör börja och sluta på en svart ruta (det spelar ingen roll var)- det beror på att vi kommer att mäta bredden på de vita rutorna, inte de svarta.

• %rita linje
• Figur 1)
• delplan (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Klicka och dra för att rita sträckan över 9 rutor, från ett svart mellanslag till ett svart mellanslag.', 'Dubbelklicka för att bekräfta.'}));
• rad = imline;
• position = vänta (rad);
• slutpunkter = line.getPosition;

Extrahera X- och Y -koodinaten för slutpunkterna för den ritade linjen.

• X = slutpunkter (:, 1)
• Y = slutpunkter (:, 2);

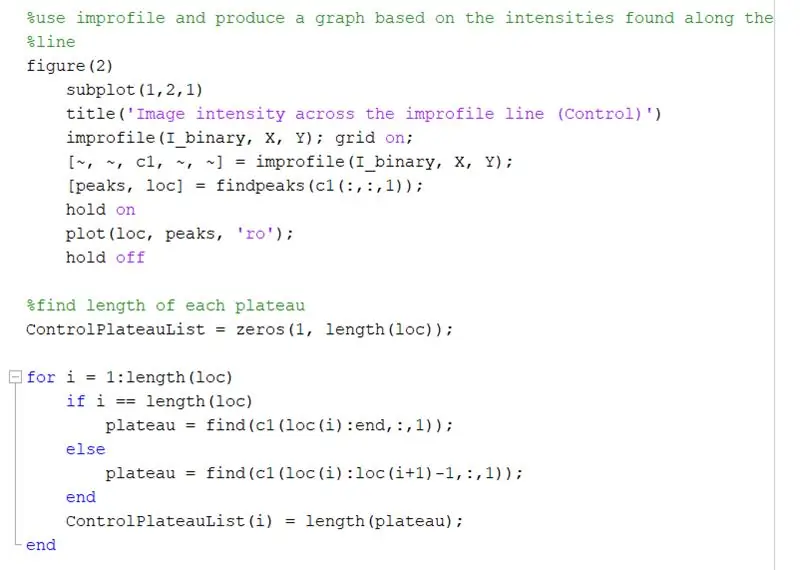
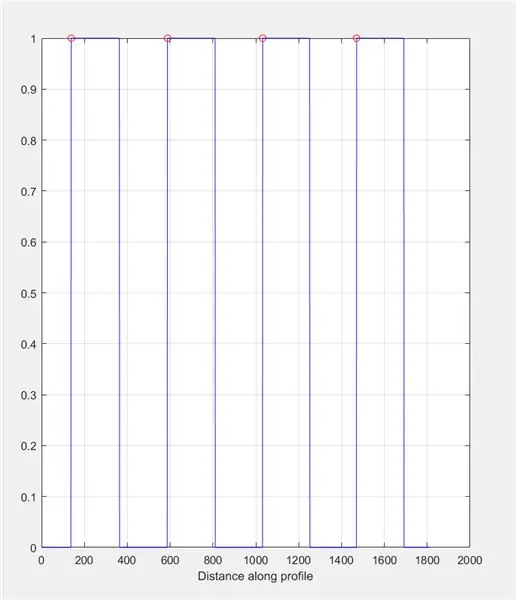
Använd improfil för att skapa en graf baserad på intensiteterna längs den ritade linjen. Detta bör likna en fyrkantvåg som sträcker sig från 0 (svart) till 1 (vit). Beräkna topparna och deras platser också.

• figur 2)
• delplan (1, 2, 1)
• titel ('Bildintensitet över den felaktiga linjen (kontroll)')
• improfil (I_binary, X, Y); rutnät på;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [toppar, loc] = findpeaks (c1 (:,:, 1));
• vänta
• plot (loc, toppar, 'ro');
• vänta

Hitta längden på varje platå på den improfila grafen med hjälp av en for loop. Kör for -slingan för samma mängd toppar som det finns i den improfila grafen. För att beräkna längden på varje platå, använd funktionen "hitta" för att hitta alla platser där det finns ett "1" istället för ett "0" intensitetsvärde. Beräkna sedan längden på den matrisen för att få platåns totala längd, som ska vara lika med bredden på en vit kvadrat i pixlar. ControlPlateauList = nollor (1, längd (loc));

för i = 1: längd (loc)

om i == längd (loc)

platå = hitta (c1 (loc (i): slutet,:, 1));

annan

platå = hitta (c1 (loc (i): loc (i+1) -1,:, 1));

slutet

ControlPlateauList (i) = längd (platå);

slutet

Steg 5: Upprepa steg 3 och 4 för testbilden

*Obs! När du ritar den felaktiga linjen på testbilden, se till att rita den över rutorna som motsvarar linjen du ritade på kontrollbilden.

Steg 6: Beräkna linsens förstoring

De förstorade mätningarna beräknas genom att dividera medelvärdet av platåns längd, som beräknades i steg 5, med medelvärdet av längden på kontrollplatån, som beräknades i steg 4. Detta beräknas vara 1,0884.

förstoring = medelvärde (plateauList)/medelvärde (ControlPlateauList);

Steg 7: Hitta R-kvadrat och användarens recept via interpolering

Använda koden:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Vi kan hitta R-kvadratvärdet för diagrammet GivenPresciption (våra linsers givna värden) mot MagArray (en uppsättning av förstoringsmätningsförhållandena som vi beräknade tidigare). Genom att ha ett tillräckligt högt R-kvadrat-värde kan man dra slutsatsen att det finns en tillräckligt stark korrelation för att motivera användningen av denna metod. För detta fall var R-kvadratvärdet 0,9912, vilket tyder på en stark korrelation och därför är motiverat att använda denna metod i analys.

Använda funktionen:

Prescription = interp1 (MagArray, GivenPrescription, förstoring, 'linjär');

Vi kan interpolera motsvarande receptvärde (på x-axeln) i vårt förstoringsförhållande (ett värde på y-axeln) och hitta vad användarens recept är.

Interpolering av data är viktigt för att denna metod ska fungera eftersom den tillåter oss att anta information som vi inte har, baserat på den information vi har. Även om en linje med bäst passform tekniskt sett skulle vara en starkare kandidat för detta antagande, skapar gränser för att minska antalet utdata samma effekt som receptglasögon kommer i inkrementella enhetliga värden i alla fall. Detta förklaras i senare steg.

Steg 8: Visa användarens recept på en graf

Använd följande kod:

• figur;
• plot (GivenPrescription, MagArray, '-g')
• vänta
• plot (recept, förstoring, 'bp')
• vänta
• rutnät
• legend ('Data', 'Interpolated Points', 'Location', 'NW')

Vi kan rita upp en graf som visar förstoringsförhållandena jämfört med det givna receptet med en grön linje och hittade data för vår beräknade förstoring jämfört med vårt interpolerade recept med en blå stjärna. Sedan märker legenden titeln, x-axeln och y-axeln och placerar legenden i det övre vänstra hörnet.

Steg 9: Begränsa ditt recept

Följande kod används för att producera avrundningen för receptet:

• om recept <= 1.125

  CalculatedPrescription = '1.0';

• elseif Recept <= 1.375

  CalculatedPrescription = '1,25';

• elseif Recept <= 1.625

  CalculatedPrescription = '1.5';

• elseif Recept <= 1.875

  CalculatedPrescription = '1,75';

• elseif Recept <= 2,25

  CalculatedPrescription = '2.0';

• elseif Recept <= 2.625

  CalculatedPrescription = '2.5';

• elseif Recept <= 3

  CalculatedPrescription = '2,75';

• elseif Recept <= 3.375

  CalculatedPrescription = '3.25';

• annan

  CalculatedPrescription = 'unknown';

• slutet

Receptet som hittas genom interpolering återspeglar inte nödvändigtvis det faktiska receptet - det beror på att det alltid kommer att finnas små variationer i analysen av fotot på grund av mänskliga misstag. Således behöver vi detta steg för att klassificera det verkliga receptet.

Recepten som ges startar vanligtvis från 1,0 dioptrier och ökar med.25 i sina recept, så efter beräkningen av receptet vill vi bestämma det recept som bäst passar vad användaren kan behöva. Efter beräkning av recept kör vi det genom de angivna If -satserna för att kontrollera dess värde och bestämma vilket recept som är nödvändigt. Allt mindre än eller lika med 1.125, då är receptet 1.0. Allt mindre än eller lika med 1,375, receptet är 1,25. Allt mindre än eller lika med 1,625, receptet är 1,5. Allt mindre än eller lika med 1.845, receptet är 1.75. Och så vidare.

Vi har värdena ökande eftersom vi kontrollerar om värdena är mindre än. Om vi gjorde att värdena minskade då det första if -uttalandet skulle läsa det första if -påståendet hela tiden. Om recept är det minsta, vill vi att det ska erkänna det som det minsta direkt, så det är därför det minsta värdet är vad vi började med. Allt som är högre än det högsta värdet betyder att receptet inte ligger inom intervallet med våra data, så det kommer att ge "Okänd" strängavläsning.