Hur man mäter högfrekvens och driftscykel, samtidigt med en mikrokontroller .: 4 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:45

Jag vet vad du tycker: "Huh? Det finns massor av instruktioner om hur man använder mikrokontroller för att mäta signalfrekvens. Gäspa." Men vänta, det finns en nyhet i den här: Jag beskriver en metod för att mäta frekvenser mycket högre än en mikrokontroller (MCU) kan bära och signalens arbetscykel - allt samtidigt!

Enhetens frekvensområde sträcker sig från ~ 43 Hz till ~ 450 kHz, medan driftscykeln sträcker sig från 1% upp till 99%.

Låt mig förklara "kan bära" -delen: en MCU mäter period för en kvadratvågssignal, T, genom att spåra tiden mellan två efterföljande övergångshändelser. Till exempel hoppar låg till hög spänning på en av dess I/O-stift. Det gör det genom att räkna antalet pulser för sin egen interna klocka. Naivt bör den övre gränsen för uppmätta frekvenser följa Nyqvist-Shannon-samplingssatsen; dvs den skulle ungefär motsvara hälften av MCU: s klockfrekvens. I själva verket är gränsen mycket, mycket lägre, eftersom MCU måste köra kod för att hantera avbrott, spara variabler, göra aritmetiska operationer, visa resultat etc. I mina experiment med en 48 MHz MCU var det minimala antalet klockcykler mellan mätbara övergångar cirka 106. Därför skulle den övre gränsen för det mätbara frekvensområdet i detta fall vara 48 000 /212 /2 = 226,4 kHz.

Medan MCU mäter signalens period kan den också bestämma dess pulsbredd, P: tiden för signalspänningen förblir hög. Med andra ord, tid mellan låg till hög och hög till låg övergång. Signalens arbetscykel definieras sedan som följande procentsats:

Tull = 100% * P / T

Precis som i fallet med frekvens finns det en praktisk gräns för pulsbredd. Med hjälp av exemplet ovan skulle 106 klockcykler begränsa pulsbredden till inte mindre än 2,21 mikrosekunder. Eller inte mindre än 50% vid 226,4 kHz.

Ett av sätten att öka den övre frekvensgränsen för kvadratvågssignaler är tillämpningen av digitala avdelare som använder flip-flops. Att dividera ingångsfrekvensen med n skulle utöka det mätbara övre intervallet n gånger. Detta är goda nyheter, digitala avdelare har en grundläggande brist: delad signal tappar information om pulsbredd (och driftcykel)! På grund av hur delarna fungerar har deras produktion alltid 50% driftscykel. Besvikelse…

På de följande sidorna kommer jag dock att visa hur man digitalt delar upp frekvensen och bevarar den ursprungliga pulsbredden så att jag kan mäta signaler långt över de gränser som direkträkning innebär.

Steg 1: Digital Frequency Division

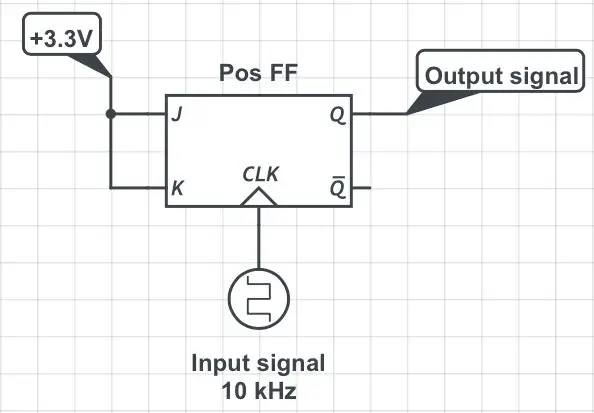
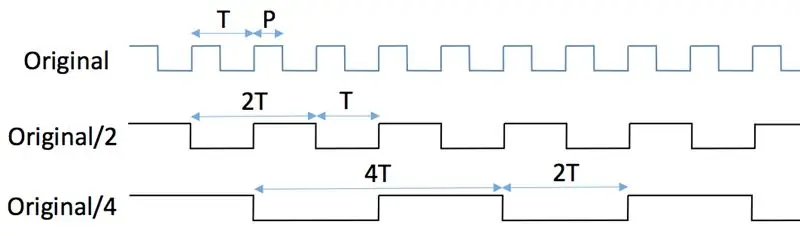
Traditionella digitala frekvensdelare använder flip-flops; denna handledning förklarar fint principer hur man konstruerar avdelare med hjälp av vanliga JK-flip-flops. Detta löser problemet med ingångsfrekvenser för höga för MCU, men har en stor nackdel: delad signal har 50% driftscykel oavsett insignalens plikt! För att se varför det är så titta på de två första figurerna. Den ursprungliga signalen med punkt T och pulsbredd P matas in i klockstiftet på en JK-flip-flop medan dess J- och K-stift alltid hålls högt (första figuren). 3.3V logik antas hela tiden. Låt oss anta att vippan utlöses av den positiva (dvs. stigande) kanten på klockan. Under dessa förhållanden sker förändringar av utgångsstiftets tillstånd (individuella "flips" och "flops") varje gång klockstiftet går från lågt till högt. Klockans höga till låga övergång (dvs. den negativa kanten) ignoreras helt. Se den andra figuren. Utgångsstiften, Q, avger en signal vars period är dubbelt så lång som den ursprungliga perioden, dvs frekvensen halveras. Utgångens pulsbredd är alltid lika med T. Följaktligen går den ursprungliga pulsbredden, P, förlorad.

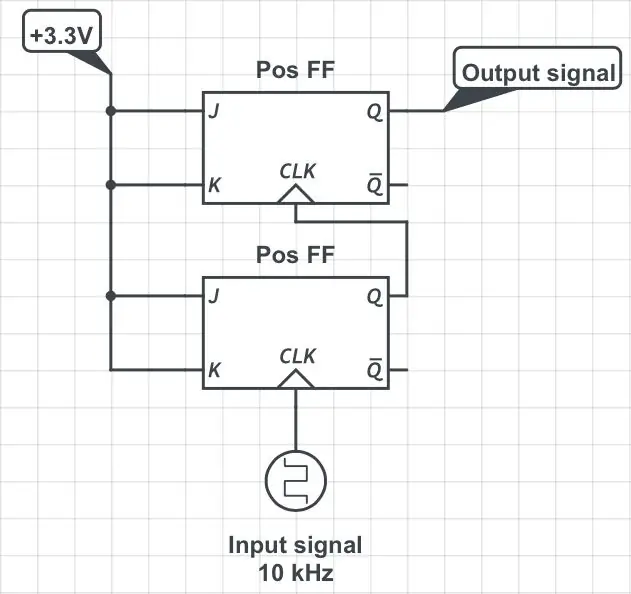
Om du lägger till ytterligare en JK-flip-flop i en konfiguration som visas i den tredje figuren divideras originalfrekvensen med 4. Om du lägger till fler flip-flops på samma sekventiella sätt divideras frekvensen med efterföljande effekter på 2: 8, 16, 32, etc.

Problem: hur delar jag en fyrkantvågs frekvens samtidigt som den bevarar dess pulsbredd?

Tanken är att korrekt lägga till en negativ kantutlöst JK-flip-flop till mixen. Låt oss kalla det "Neg FF"; se fjärde figuren. Här betyder "ordentligt" att J- och K-stiften i den nya vippan är knutna till Q respektive Qbar-utgångsstiften i divider-by-4 ("Pos FF") som visas i föregående figur. (Här är "bar" den horisontella stapeln över Q -symbolen som indikerar logisk negation.) För att se vad detta uppnår, ta en titt på funktionstabellen för "Neg FF" i den femte siffran: Negs utgångsstift, Q och Qbar, speglar tillståndet för dess ingångsstift, J respektive K. Vilket betyder att de speglar tillståndet för Pos 'Q och Qbar. Men Neg's flip-flop-åtgärd måste vänta på den negativa kanten av den ursprungliga signalen, som kommer vid tidpunkten P efter den positiva kanten. A ha!

De resulterande vågformerna illustreras i den sjätte figuren. "Pos Q" -utgångar signalerar vid 1/4 frekvens, "Pos Qbar" är det omvänt, "Neg Q" följer "Pos Q" skiftat med pulsbredd P och "Neg Qbar" är dess invers. Du kan verifiera att det logiska OCH för "Pos Qbar" och "Neg Q" producerar ett pulståg som kännetecknas av den ursprungliga pulsbredden P och 1/4 av frekvensen. Bingo!

Först använde jag exakt denna utsignal för att mata MCU: n. Det visade sig dock vara problematiskt för mycket korta pulsbredder på grund av MCU: s 106 cyklerbegränsning som nämns i introduktionen. Jag har löst detta lilla problem genom att välja en annan utdata: "Pos Qbar" OCH "Neg Qbar" istället. En titt på vågformerna bör övertyga dig om att pulsbredden för denna specifika vågform, P ', varierar mellan T och 2T istället för (0, T) intervall för P. P kan enkelt återvinnas från P' genom att:

P = 2T - P '

Steg 2: Rekommenderad hårdvara

Jag gillar verkligen den relativa nykomlingen till elektroniska hobbyister: Atmel SAM D21 MCU: er baserade på 32-bitars ARM Cortex M0+ -processorn som arbetar med 48 MHz klockfrekvens, mycket högre än de äldre Atmels. Till det här projektet köpte jag:

• ItsyBitsy M0 Express MCU -bräda från Adafruit
• Jag råkade ha ett laddningsbart LiPo -batteri från Adafruit
• Monokrom 128x32 SPI OLED -skärm (du gissade det: Adafruit)
• Dubbel positiv kant-utlöst JK flip-flop SN74HC109 från Texas Instruments
• Dubbel negativ kant-utlöst JK flip-flop SN74HC112 från Texas Instruments
• Fyrbädds OCH gate CD74AC08E från Texas Instruments
• Fyrbädds ELLER gate CD74AC32E från Texas Instruments

Steg 3: Kretsen

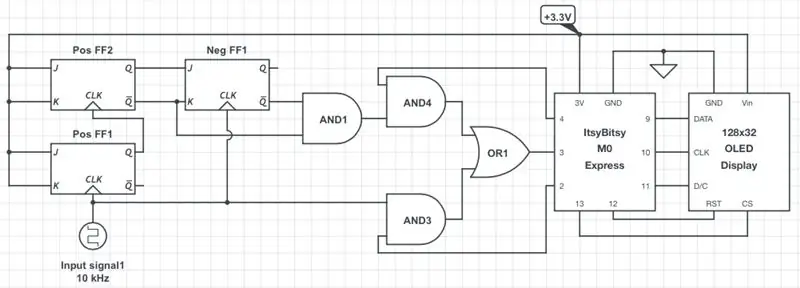
Den första figuren visar en förenklad schema över frekvens/driftmätaren. 3.3 V CMOS -logiken antas hela tiden. Följaktligen måste den ingående kvadratvågens amplitud ligga mellan motsvarande V_IH nivå (dvs. 2 V) och 3,3 V. Om inte, måste du skala upp eller ner i enlighet därmed. I de flesta fall räcker det med en enkel spänningsdelare. Om du vill designa din version av mätaren på en annan logisk nivå måste du använda en annan mikrokontroller (MCU), batteri och en display som fungerar på önskad nivå. De logiska grindarna och vipporna som används i detta projekt fungerar med logiska nivåer var som helst mellan 2 V och 6 V och borde vara OK i de flesta fall.

Som visas använder ItsyBitsy MCU stiften 9-13 för att kommunicera med displayen via programvarans SPI-protokoll. 3V -stiftet levererar ström till hela kretsen. Digital ingångsstift 3 accepterar den analyserade signalen, medan stift 2 och 4 styr signalkällan: antingen direkt signal som kommer genom grind AND3 (låga ingångsfrekvenser) eller signal dividerad med 4 genom grind AND4 (höga ingångsfrekvenser) enligt beskrivning i steg 2 Koden, som diskuteras i nästa steg, detekterar automatiskt det inkommande frekvensområdet och ändrar på lämpligt sätt signalkällan.

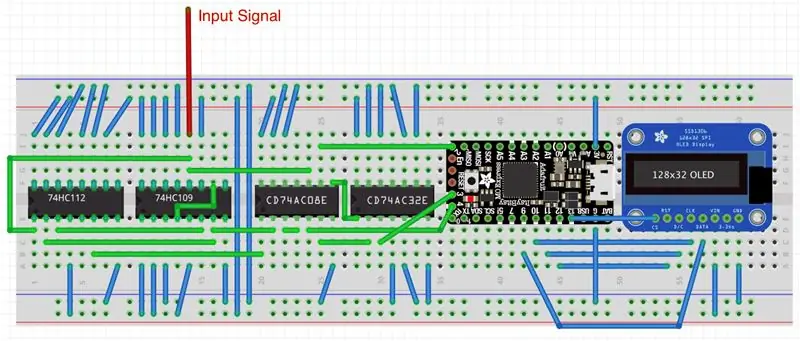
Schemat visar inte den sanna komplexiteten hos digitala chip -anslutningar. Den andra bilden visar hur projektet skulle se ut på en brödbräda. Ingångssignalen kommer via en röd tråd till 2CLK-stiftet på den dubbla positiva kant-vippan. FÖRSIKTIGHET: Normalt bör alla J- och K -stift på denna flip -flop hållas högt, men särskilt SN74HC109 har Kbar -stiftet - ett inverterat K -stift - istället. Därför måste denna stift jordas! Den första negativa flip-floppen i SN74HC112 har sin 1K- och 1J-stift ansluten till 1Q- och 1Qbar-stiften i SN74HC109. Den andra vippan i SN74HC112 är oanvänd och dess ingångspinnar (2K, 2J, 2CLRbar) är jordade. Alla andra extra stift PREbar (förinställd) och CLRbar (klar) i alla flip-flops måste anslutas till logiskt högt. Oanvänd klocka och utgångsstiften lämnas okopplade. På samma sätt jordas oanvända ingångsstiften i alla grindar, medan oanvända utgångsstift inte är anslutna. Som jag diskuterade i min "Invisible Killer of the Phone Ring" Instruerbar, eliminerar jordade oanvända ingångspinnar på logiska chips slumpmässiga svängningar och sparar batterikraft.

Steg 4: Koden och mätning av låga frekvenser

Naturligtvis sker all handling i koden som är länkad nedan. När ingången som kommer in på stift 3 växlar från digital låg till hög, börjar MCU räkna pulser för sin interna 48 MHz klocka. Den noterar ögonblicket för hög till låg övergång och fortsätter räkningen tills nästa låg till hög omkopplare, när den startar om hela processen igen. Den första räkningen representerar pulsbredd, medan hela räkningen representerar signalens period. Och det är hela hemligheten.

CPU: n noterar dessa övergångar via maskinvaruavbrott. SAMD21 har flera klockor; min kod använder TC3 one. Inledningsvis har jag börjat med att läsa M0: s databladstöd för mycket arbete med att koda avbrottshanteraren, men snart har jag upptäckt en mycket relaterad kod i Arduino Forum -inlägg av användare electro_95, MartinL och Rucus vars bidrag är vederbörligen erkänt. Jag införlivade och modifierade deras kombinerade kod i min; sparar mig mycket tid!

Som jag tidigare nämnde är signalupplösningen begränsad av ~ 106 CPU -cykler för att köra kod mellan avbrott. Digital division med pulsbreddskonservering tar hand om höga frekvenser. Låga frekvenser, å andra sidan, utgör en annan utmaning: eftersom TC3 -klockräknaren är 16 bitar lång, överflödar den efter att ha passerat gränsen för 65, 536 räkningar. Man kan hantera denna situation genom att lägga till ett överflödsavbrott, men valde en annan lösning: TC3 kan använda en förskalad (dvs. programvaruindelad) CPU-klocka istället för hårdvaran 48 MHz. Således, om signalens period närmar sig överskridningsgränsen, kan koden instruera TC3 att använda 24 MHz -räkningar för nästa period och, voila, räknaren sjunker under 32, 768 räkningar. För ännu lägre frekvenser kan TC3 instrueras att räkna 12 MHz pulser etc. Lämplig förkalkning bestäms automatiskt baserat på signalens frekvens, med hysteres, för att hålla TC3 -räknaren inom överflödsgränsen. Som ett resultat är den nedre änden av enhetens intervall cirka 43 Hz.

Du är välkommen att gaffla koden och använda den i ditt projekt, men ange dess källa när du publicerar resultat.

Länk till koden.