Innehållsförteckning:
- Steg 1:
- Steg 2:
- Steg 3: Spännings- och strömfasordiagram för vågformerna
- Steg 4: Ström-, motstånds- och spänningsfasvinklar för serie RC -kretsar
- Steg 5: Impedans och fasvinkel för serie RC -kretsar
- Steg 6: Variation av impedans med frekvens
- Steg 7: Variation av impedans och fasvinkel med frekvens
- Steg 8: En illustration av hur Z och XC förändras med frekvens
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:37.
- Senast ändrad 2025-01-23 15:10.

RC -kretsar
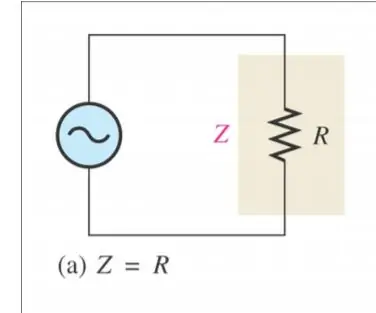
Impedans: är vad källan "ser" som totalt motstånd mot ström
Metoden för beräkning av impedans skiljer sig från en krets
Steg 1:

När en krets är rent kapacitiv (innehåller endast kondensator) är fasvinkeln mellan applicerad spänning och total ström 90 ° (strömledningar)
Steg 2:

När det finns en kombination av både resistans och kapacitans i en krets är fasvinkeln mellan resistans (R) och kapacitiv reaktans (XC) 90 ° och fasvinkeln för total impedans (Z) är någonstans mellan 0 ° och 90 °
När det finns en kombination av både motstånd och kapacitans i en krets är fasvinkeln mellan totalström (IT) och kondensatorspänningen (VC) 90 ° och fasvinkeln mellan den applicerade spänningen (VS) och den totala strömmen (IT) är någonstans mellan 0 ° och 90 °, beroende på relativa värden för resistans och kapacitans
Steg 3: Spännings- och strömfasordiagram för vågformerna

Steg 4: Ström-, motstånds- och spänningsfasvinklar för serie RC -kretsar

Steg 5: Impedans och fasvinkel för serie RC -kretsar

- I serien RC -krets är den totala impedansen fasorsumman av R och Xc
- Impedansstorlek: Z = √ R^2 + Xc^2 (vektorsumma)
- Fasvinkel: θ = tan-1 (X C/R)
Varför använder vi vektorsumma inte algebraisk summa?
Svar: Eftersom motstånd inte fördröjer spänningen, men kondensatorn gör det.
Så Z = R+Xc är fel.
Tillämpningen av Ohms lag på en hel serie RC -krets innebär användning av mängderna Z, Vs och Itot som:
Itot = Vs/Z Z = Vs/Itot Vs = Itot * Z
Glöm inte heller:
Xc = 1/2πFC
Steg 6: Variation av impedans med frekvens

Steg 7: Variation av impedans och fasvinkel med frekvens

Steg 8: En illustration av hur Z och XC förändras med frekvens

R förblir konstant
Rekommenderad:
Arduino Car Reverse Parking Alert System - Steg för steg: 4 steg

Arduino Car Reverse Parking Alert System | Steg för steg: I det här projektet kommer jag att utforma en enkel Arduino Car Reverse Parking Sensor Circuit med Arduino UNO och HC-SR04 Ultrasonic Sensor. Detta Arduino -baserade bilomvändningsvarningssystem kan användas för autonom navigering, robotavstånd och andra
Steg för steg PC -byggnad: 9 steg

Steg för steg PC -byggnad: Tillbehör: Hårdvara: ModerkortCPU & CPU -kylarePSU (strömförsörjningsenhet) Lagring (HDD/SSD) RAMGPU (krävs inte) CaseTools: Skruvmejsel ESD -armband/mathermisk pasta med applikator
Tre högtalarkretsar -- Steg-för-steg handledning: 3 steg

Tre högtalarkretsar || Steg-för-steg-handledning: Högtalarkretsen förstärker ljudsignalerna som tas emot från miljön till MIC och skickar den till högtalaren varifrån förstärkt ljud produceras. Här visar jag dig tre olika sätt att göra denna högtalarkrets med:
Steg-för-steg-utbildning i robotik med ett kit: 6 steg

Steg-för-steg-utbildning i robotik med ett kit: Efter ganska många månader av att bygga min egen robot (se alla dessa), och efter att två gånger ha misslyckats med delar, bestämde jag mig för att ta ett steg tillbaka och tänka om min strategi och riktning. De flera månaders erfarenhet var ibland mycket givande och
Akustisk levitation med Arduino Uno Steg-för-steg (8-steg): 8 steg

Akustisk levitation med Arduino Uno Steg-för-steg (8-steg): ultraljudsgivare L298N Dc kvinnlig adapter strömförsörjning med en manlig DC-pin Arduino UNOBreadboardHur det fungerar: Först laddar du upp kod till Arduino Uno (det är en mikrokontroller utrustad med digital och analoga portar för att konvertera kod (C ++)
