
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:46.
- Senast ändrad 2025-01-23 15:11.

Hej! För att tillfredsställa mitt intresse för programmering och förhoppningsvis hjälpa till att tillfredsställa ditt, skulle jag vilja visa dig en 3D Viewer som jag kodade i javascript. Om du vill öka din förståelse för 3D -spel eller till och med skapa ditt eget 3D -spel är denna prototyp 3D -visning perfekt för dig.
Steg 1: Teorin

För att förstå teorin om denna 3D -visare kan du helt enkelt undersöka hur du ser på din omgivning (det hjälper att bara ha en betydande ljuskälla). Lägg märke till att:
- Objekt som ligger längre bort från dig tar upp en mindre del av ditt synfält.
- Objekt som ligger längre bort från ljuskällan verkar mörkare i färgen.
- När ytorna blir mer parallella (mindre vinkelräta) till ljuskällan verkar de mörkare i färgen.
Jag bestämde mig för att representera ett synfält med ett gäng linjer som härrör från en enda punkt (analogt med ögongloben). Liksom en spikboll måste linjerna vara jämnt fördelade för att säkerställa att varje del av synfältet är lika representerat. På bilden ovan, lägg märke till hur linjerna som kommer från spikbollen blir mer åtskilda när de rör sig längre bort från bollens mitt. Detta hjälper till att visualisera programmets implementering av observation 1 eftersom tätheten av linjer minskar när objekt rör sig längre bort från mittpunkten.
Linjerna är den grundläggande synenheten i programmet, och de mappas var och en till en pixel på displayen. När en linje skär ett objekt färgas motsvarande pixel baserat på dess avstånd från ljuskällan och dess vinkel från ljuskällan.
Steg 2: Implementeringsteori

För att förenkla programmet är ljuskällan densamma som mittpunkten (ögongloben: punkten från vilken kartan ses och var linjerna härstammar). Analogt med att hålla ett ljus intill ditt ansikte, eliminerar detta skuggor och gör att ljusstyrkan för varje pixel kan beräknas mycket lättare.
Programmet använder också sfäriska koordinater, med centrum för synen vid ursprunget. Detta gör att linjerna enkelt kan genereras (var och en med en unik theta: horisontell vinkel och phi: vertikal vinkel), och utgör grunden för beräkningar. Rader med samma theta mappas till pixlar i samma rad. Phis för motsvarande vinklar ökar över varje rad pixlar.
För att förenkla matematiken består 3D-kartan av plan med en gemensam variabel (gemensam x, y eller z), medan de två andra icke-vanliga variablerna är begränsade inom ett intervall och kompletterar definitionen av varje plan.
För att se sig omkring med musen, faktorens ekvationer faktor i en vertikal och horisontell rotation under konverteringen mellan sfäriska och xyz koordinatsystem. Detta har effekten av att förforma en rotation på "spikebollen" uppsättningen synlinjer.
Steg 3: Matematik
Följande ekvationer gör att programmet kan avgöra vilka linjer som skär varje objekt och information om varje skärningspunkt. Jag härledde dessa ekvationer från de grundläggande sfäriska koordinatekvationerna och 2D -rotationsekvationerna:
r = avstånd, t = theta (horisontell vinkel), p = phi (vertikal vinkel), A = rotation om Y -axeln (vertikal rotation), B = rotation om Z -axeln (horisontell rotation)
Kx = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*cos (B) -sin (p)*sin (t)*sin (B)
Ky = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*sin (B)+sin (p)*sin (t)*cos (B)
Kz = -sin (p)*cos (t)*sin (A)+cos (p)*cos (A)
x = r*Kx
y = r*Ky
z = r*Kz
r^2 = x^2+y^2+z^2
belysning = Klight/r*(Kx eller Ky eller Kz)
p = arccos ((x*sin (A)*cos (B)+y*sin (A)*sin (B)+z*cos (A))/r)
t = arccos ((x*cos (B)+y*sin (B) -p*sin (A)*cos (p))/(r*cos (A)*sin (p)))
Steg 4: Program

Jag hoppas att denna prototyp 3D -visare hjälpte dig att förstå hur virtuella 3D -verkligheter fungerar. Med lite mer perfektion och kodning har den här tittaren verkligen potential att användas i 3D -spelutveckling.
Rekommenderad:
Film Negativ Viewer och Converter: 8 steg (med bilder)

Film Negative Viewer and Converter: Jag fann ett omedelbart behov av att snabbt kunna se och spela in gamla filmnegativ. Jag hade flera hundra att sortera igenom … Jag inser att det finns olika appar för min smarta telefon men jag kunde inte få tillfredsställande resultat så det här är vad jag cam
Arduino Baby Monitor med Java Viewer: 8 steg (med bilder)
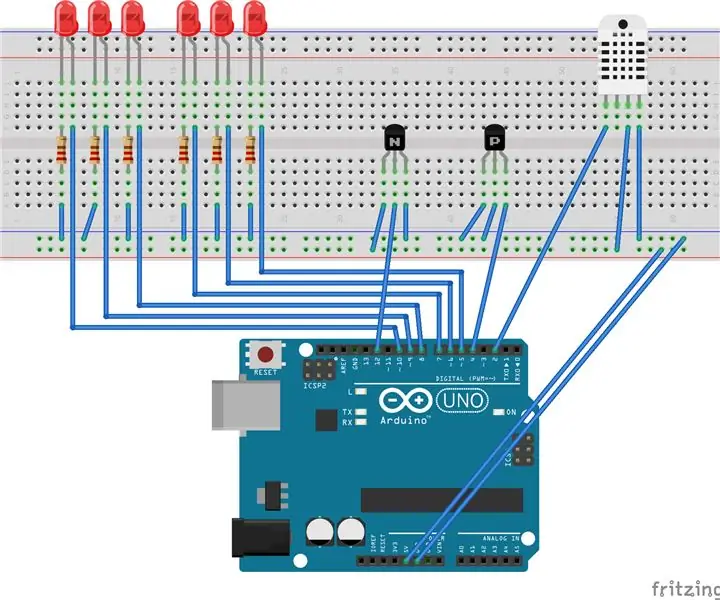
Arduino Baby Monitor med Java Viewer: Bygg en Arduino-baserad multisensorenhet för att observera förhållandena i ett rum. Denna enhet känner av fukt, temperatur, rörelse och ljud. Bifogad är en java -baserad tittare som tar emot seriell data från arduino
Headup Web Cam Viewer: 7 steg

Headup Web Cam Viewer: En ny post tittade på ett kommersiellt system för att tillåta användare att titta direkt på sin webbkamera samtidigt som de fortfarande kan se personen de pratar med - Teleprompter -stil - Detta är min uppfattning om den idén. Det är lätt att konstruera som viktigt
Photo Viewer Handledsvärmare: 5 steg

Photo Viewer Handledsvärmare: Jag köpte en av dessa nyckelringfotovisare, det var bara en tenner så jag tänkte "ja varför inte, kanske skulle kunna hacka det till något coolt" .Så det dyker upp och det första jag gör med den? Dra isär den och stick in den i en handledsvärmare
Digital 3D Picture Viewer - "The DigiStereopticon": 6 steg (med bilder)

Digital 3D Picture Viewer - "The DigiStereopticon": Stereoskopisk fotografering har fallit i onåd. Detta beror troligen på det faktum att människor inte gillar att behöva bära speciella glasögon för att se familjens ögonblicksbilder. Här är ett roligt litet projekt du kan göra på mindre än en dag för att göra din 3D -bild
