Förstå kanalblandning: 4 steg (med bilder)

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:46

Om du någonsin har kört ett fjärrkontrollchassi finns det en god chans att du har använt blandning, även om du inte visste det. Specifikt, om du har använt en enda joystick eller gimble för att styra ett fordon som använder skridstyrning eller differentialstyrning, har du använt blandning.

Blandning är helt enkelt hur data från din joystick används för att bestämma hur mycket ström som ska tillföras till varje sida av chassit.

Om du öppnar en joystick ser du vanligtvis två potentiometrar inuti. En för att mäta din nuvarande position längs Y -axeln (upp och ner), och den andra för att mäta var du befinner dig längs X -axeln (från sida till sida).

Även om jag inte har någon formell utbildning i ämnet har jag varit tvungen att blanda in kod tidigare och nyligen ville jag dyka lite djupare in i ämnet.

Först vill jag notera att de flesta RC -sändare har blandningsförmåga liksom många motorstyrenheter. Denna information kommer att vara mest användbar om du måste göra blandningen själv i din kod. Säg till exempel om du använder en Arduino för att läsa omixad data från en RC -mottagare, eller om du läser analog data från krukorna i en joystick, eller om du läser koordinaterna från en digital joystick i en mobilapp.

Låt oss ta en titt på några olika blandningsmetoder.

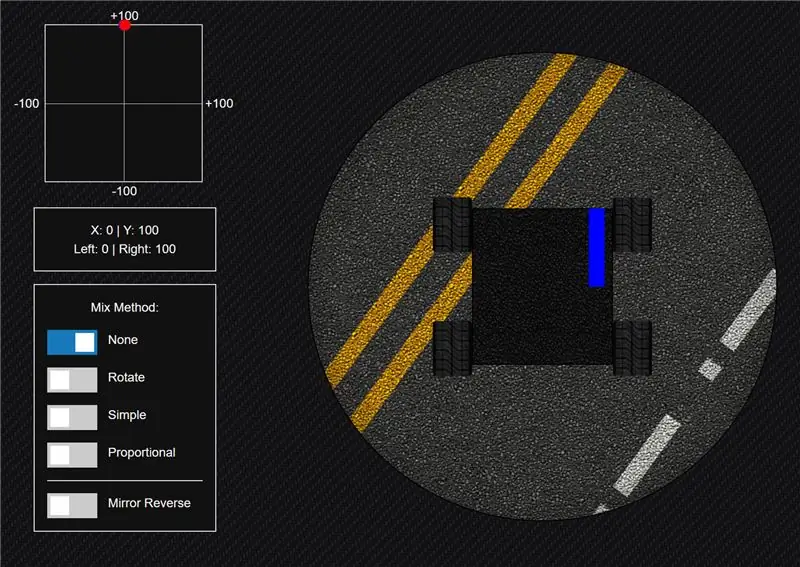
Steg 1: Blandningsmetod »Ingen

Låt oss först titta på vad som händer om du inte använder blandning alls. Om du bara skickar data från ena axeln till ena sidan av chassit och den andra axeln till den andra sidan, svarar ditt fordon inte som du vill.

Om du till exempel trycker joysticken rakt fram, är Y -axeln vid full gas och X -axeln är 0. Så du skulle köra i cirklar istället för att gå rakt.

Steg 2: Metod Metod »Rotera

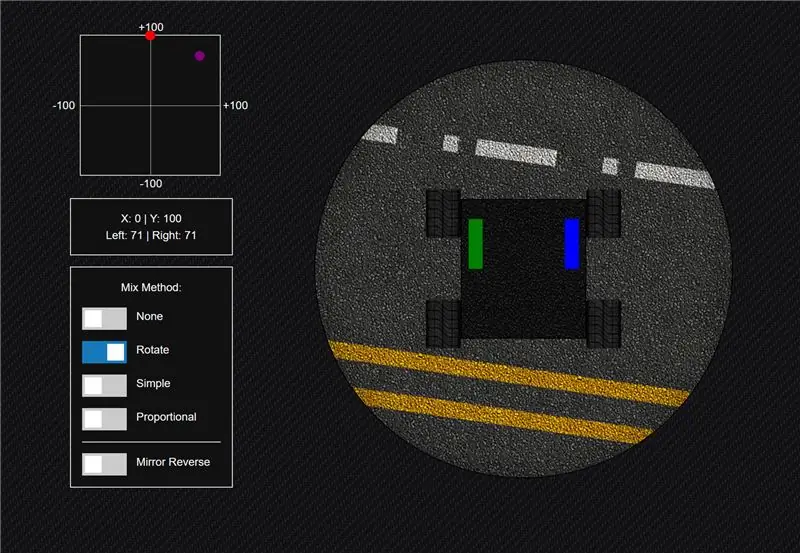
En arbetskamrat påpekade mig en gång att du med en nypa kan rotera din sändare 45 grader för en fattig mans blandning. Om du tänker på värdena från de två potentiometrarna i en joystick som x och y -axeln på ett rutnät (med båda axlarna som sträcker sig -100 till +100) är det mycket meningsfullt eftersom du kommer till +100 på båda axlarna när du trycker joysticken uppåt och åt höger. Så om det här kartlägger direkt till dina två chassikanaler (vänster och höger sida av din robot) skulle det få din robot att gå framåt.

Så den första blandningsmetoden jag någonsin försökt var att matematiskt rotera x- och y -koordinaten 45 grader kring rutans mittpunkt.

Detta fungerar ok, men jag kan inte gå framåt med 100% effekt eftersom när du roterar begränsas den totala rörelsen till en cirkel i rutnätet, vilket innebär att du aldrig riktigt kan komma in i det övre högra hörnet.

Detta resulterar också i att hörnen på nätet inte utnyttjas. Detta är inte ett problem om du använder en joystick/gimple som begränsar din rörelse så att dessa områden aldrig nås i alla fall, men annars vill du att den delen av rutnätet gör något så att dina rörelser känns helt proportionella.

Om du är en visuell lärare som jag själv kan det här konceptet vara lättare att grop genom att titta på videon i början av denna instruerbara.

Låt oss titta på några kodexempel.

ANMÄRKNINGAR OM MINE KODEXEMPEL: Jag utelämnar hur du får joystick_x- och joystick_y -värdena eftersom det skulle förändras beroende på ditt projekt. Jag kommer också att kartlägga/begränsa till ± 100 men du kan troligtvis behöva karta till 1000 - 2000 för PWM eller 0 - 255 för analog utgång etc. Jag begränsar alltid … för säkerhets skull.

Arduino Exempel:

// matematiskt rotera

dubbel rad = -45*M_PI/180; int leftThrottle = joystick_x * cos (rad) - joystick_y * sin (rad); int rightThrottle = joystick_y * cos (rad) + joystick_x * sin (rad); // constrain leftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = begränsning (rightThrottle, -100, 100);

JavaScript -exempel:

// matematiskt rotatevar rad = -45*Math. PI/180; leftThrottle = joystick_x * Math.cos (rad) - joystick_y * Math.sin (rad); rightThrottle = joystick_y * Math.cos (rad) + joystick_x * Math.sin (rad); // constrainleftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = constrain (rightThrottle, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };

Steg 3: Metod Metod »Enkel

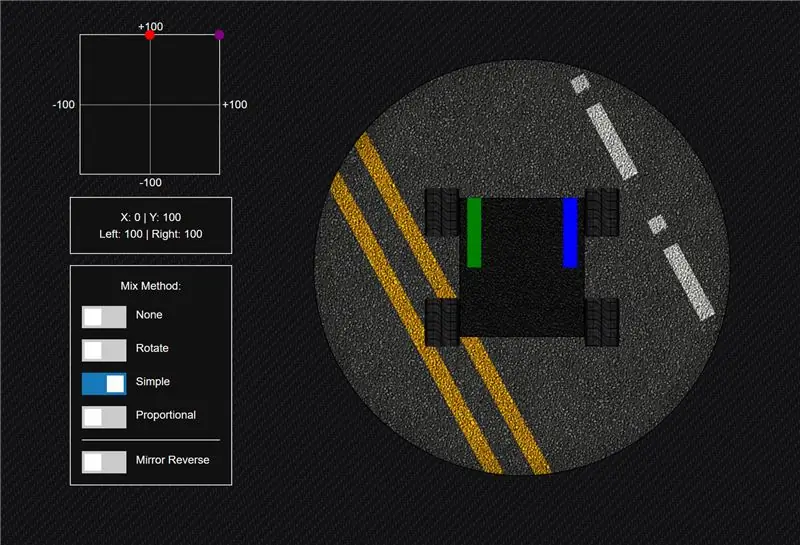
Därefter har vi en mycket enkel ekvation som jag först plockade upp från en av Shawn Hymels Adventures in Science SparkFun -videor där han råkade arbeta med ett projekt som liknade det jag arbetade med.

Denna ekvation låter dig komma till full fart när du går framåt, men ungefär som rotationsmetoden bortser du från hörnområdena i rutnätet. Detta beror på att i vissa fall är max 100 och i vissa fall max 200. Så du skulle använda en begränsningsfunktion för att bortse från allt efter 100.

Och förresten kallar jag inte det här förnedrande … det finns en skönhet i enkelheten.

Arduino Exempel:

int leftThrottle = joystick_y + joystick_x;

int rightThrottle = joystick_y - joystick_x; // constrain leftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = begränsning (rightThrottle, -100, 100);

JavaScript -exempel:

var leftChannel = joystick_y + joystick_x;

var rightChannel = joystick_y - joystick_x; // constrain leftChannel = constrain (leftChannel, -100, 100); rightChannel = begränsning (rightChannel, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };

Steg 4: Metodmetod »Proportional

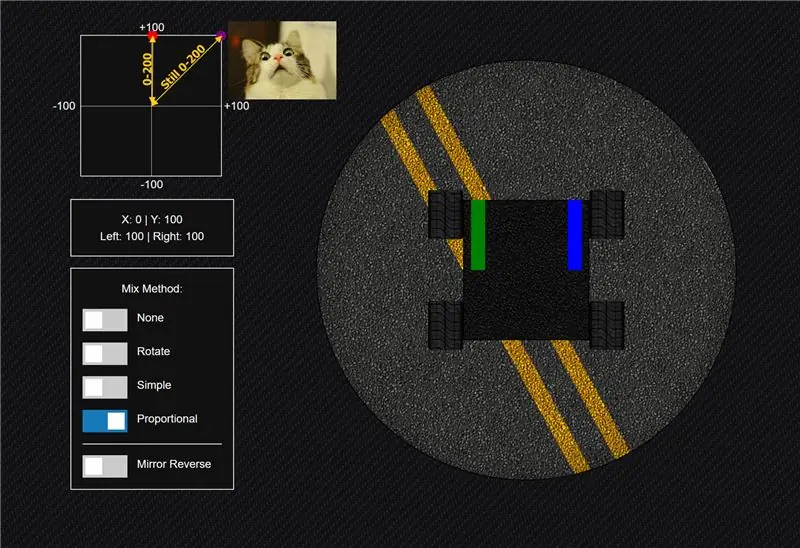
Jag hoppade av den enkla metoden i hopp om att göra det bästa av båda världens ekvation. Tanken här är att vara fullt proportionell i alla riktningar även diagonalt trots att du rör dig ett större avstånd men har samma räckvidd som när du rör dig vertikalt vilket är ett mindre avstånd.

Du slutar med en skala från -200 till +200 i alla riktningar i mina exempel. Jag kartlägger det till ± 100 eftersom det representerar procentandelen effekt som går till varje kanal - men du kommer att vilja kartlägga det till det som fungerar i din användning- fodral till din motorstyrenhet. Om du till exempel skickar en PWM-signal kan du mappa den till 1000 till 2000 eller om du skickar en analog signal kan du mappa den till 0-255 och ange riktningen som boolean etc.

Arduino Exempel:

int leftThrottle = joystick_y + joystick_x;

int rightThrottle = joystick_y - joystick_x; // i vissa fall är max 100, i vissa fall är det 200 // låt oss faktorera skillnaden så max är alltid 200int diff = abs (abs (joystick_y) - abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle - diff: rightThrottle + diff; // Karta från ± 200 till ± 100 eller vilket intervall du behöver leftThrottle = map (leftThrottle, 0, 200, -100, 100); rightThrottle = map (rightThrottle, 0, 200, -100, 100); // constrainleftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = constrain (rightThrottle, -100, 100);

JavaScript -exempel:

var leftThrottle = joystick_y + joystick_x; var rightThrottle = joystick_y; joystick_x; // i vissa fall är max 100, i vissa fall är det 200, // låt oss ta med skillnaden så max är alltid 200var diff = Math.abs (Math.abs (joystick_y) - Math.abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle -diff: rightThrottle + diff; // Karta från ± 200 bakåt ner till ± 100 eller vad du än behöver leftThrottle = map (leftThrottle, -200, 200, -100, 100); rightThrottle = map (rightThrottle, -200, 200, -100, 100); // constrain leftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = constrain (rightThrottle, -100, 100); // some helper functionsvar constrain = function (num, min, max) {return Math.min (Math. max (num, min), max); }; var map = function (num, inMin, inMax, outMin, outMax) {var p, inSpan, outSpan, mapped; inMin = inMin + inMax; num = num + inMax; inMax = inMax + inMax; inSpan = Math.abs (inMax-inMin); p = (num/inSpan)*100; outMin = outMin + outMax; outMax = outMax + outMax; outSpan = Math.abs (outMax - outMin); mapped = outSpan*(p/100) - (outMax/2); retur mappad;};