Självbalanseringsrobot med PID -algoritm (STM MC): 9 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:46

Nyligen har mycket arbete gjorts i självbalansering av föremål. Begreppet självbalansering började med balansering av inverterad pendel. Detta koncept utvidgades även till design av flygplan. I detta projekt har vi utformat en liten modell av självbalanseringsrobot med PID -algoritmen (Proportional, Integral, Derivative). Sedan dess är denna metod det nya ansiktet på de industriella processstyrsystemen. Denna rapport går igenom metoderna för självbalansering av objekt. Detta projekt genomfördes som ett terminsprojekt för att förstå korrelationen mellan PID och effektiviteten hos olika industriella processer. Här fokuserar vi bara på att ge en kort genomgång av effektiviteten och tillämpningen av PID -kontrollen. Detta dokument har utvecklats genom att ge en kort introduktion till styrsystem och relaterade terminologier, utöver motivationen för projektet. Experiment och observationer har gjorts, meriter och nackdelar beskrivits med slut på de framtida förbättringarna. En modell för självbalanserande robot utvecklades för att förstå PID: s effektivitet i styrsystemet. Genom att genomgå några noggranna tester och experiment upptäcktes fördelarna och nackdelarna med PID -kontrollsystemet. Det visade sig att trots detta många fördelar med PID -kontroll över tidigare metoder, kräver detta system fortfarande många förbättringar. Det hoppas att läsaren får en god förståelse för vikten av självbalansering, effektiviteten och bristerna i PID -kontroll

Steg 1: Introduktion

Med tillkomsten av datorer och industrialiseringen av processer, genom människans historia, har det alltid funnits forskning för att utveckla sätt att finjustera processer och ännu viktigare, att kontrollera dem med hjälp av maskiner autonomt. Syftet är att minska människans engagemang i dessa processer och därigenom minska felet i dessa processer. Därför utvecklades fältet”Control System Engineering”. Styrsystemsteknik kan definieras som att använda olika metoder för att styra hur en process fungerar eller underhålla en konstant och föredragen miljö, vare sig det är manuellt eller automatiskt.

Ett enkelt exempel kan vara att kontrollera temperaturen i ett rum. Manuell kontroll betyder närvaron av en person på en plats som kontrollerar de nuvarande förhållandena (sensorn), jämför det med det önskade värdet (bearbetning) och vidtar lämpliga åtgärder för att få det önskade värdet (ställdon). Problemet med den här metoden är att den inte är särskilt tillförlitlig eftersom en person är benägen för fel eller försumlighet i sitt arbete. Ett annat problem är också att hastigheten på processen som initieras av ställdonet inte alltid är enhetlig, vilket innebär att det ibland kan ske snabbare än nödvändigt eller ibland kan det vara långsamt. Lösningen på detta problem var att använda en mikrokontroller för att styra systemet. Mikrostyrenheten är

programmerad för att styra processen, enligt givna specifikationer, anslutna i en krets (diskuteras senare), matade det eller de önskade värdena och kontrollerar därigenom processen för att bibehålla det önskade värdet. Fördelen med denna process är att ingen mänsklig intervention krävs i denna process. Dessutom är processens hastighet likformig

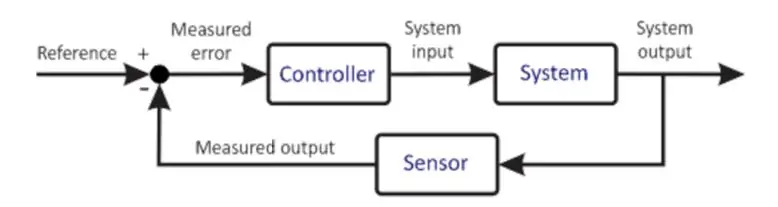
Grundläggande styrsystem

Det föregående diagrammet visar en mycket förenklad version av ett styrsystem. Mikrokontrollern är kärnan i alla kontrollsystem. Det är en mycket viktig komponent, därför bör dess val av val göras noggrant utifrån systemkraven. Mikrostyrenheten tar emot en ingång från användaren. Denna ingång definierar önskat tillstånd för systemet. Mikrostyrenheten får också en återkopplingsingång från sensorn. Denna sensor är ansluten till systemets utgång, vars information matas tillbaka till ingången. Mikroprocessorn, baserad på sin programmering, utför olika beräkningar och ger en utmatning till ställdonet. Ställdonet, baserat på utgången, styr anläggningen för att försöka upprätthålla dessa förhållanden. Ett exempel kan vara en motorförare som kör en motor där motorföraren är ställdonet och motorn är anläggningen. Motorn roterar alltså med en given hastighet. Den anslutna sensorn läser anläggningens tillstånd för närvarande och matar den tillbaka till mikrokontrollen. Mikrostyrenheten jämför igen, gör beräkningar och därmed upprepar sig cykeln. Denna process är repetitiv och oändlig, varigenom mikrokontrollern upprätthåller de önskade förhållandena

Steg 2: PID -baserat kontrollsystem

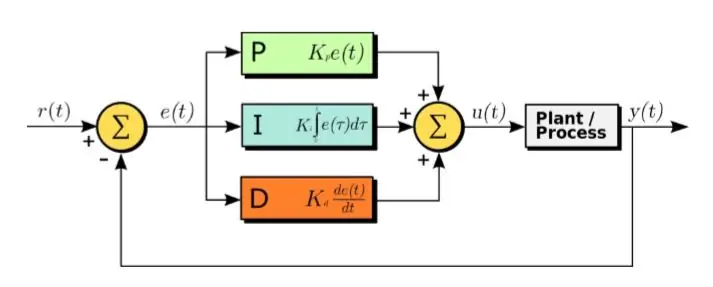
PID -algoritmen är en effektiv metod för att utforma ett styrsystem.

Definition

PID står för Proportional, Integral and Derivative. I denna algoritm är den mottagna felsignalen ingången. Och följande ekvation appliceras på felsignalen

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integral (e (t)) (1.1)

Kort förklaring

Såsom framgår av ekvationen ovan beräknas integralen och derivatet av felsignalerna, multipliceras med sina respektive konstanter och adderas tillsammans med konstanten Kp multiplicerad med e (t). Utmatningen matas sedan till ställdonet som gör att systemet körs. Nu kan vi titta på varje del av funktionen i tur och ordning. Denna funktion påverkar direkt stigningstid, falltid, topp över skjutning, avvecklingstid och steady state -fel.

• Proportional del: Proportionell del minskar stigningstiden och minskar steady state -felet. Detta innebär att systemet kommer att ta mindre tid att nå sitt toppvärde och när det når sitt steady state blir steady state -felet lågt. Det ökar dock toppöverskottet.

• Derivatdel: Derivatdelen reducerar överskridandet och avvecklingstiden. Detta innebär att systemets övergående tillstånd kommer att dämpas mer. Systemet kommer också att nå sitt stabila tillstånd på mindre tid. Det har dock ingen effekt på stigningstiden eller steady state -felet.

• Integrerad del: Den integrerade delen reducerar stigningstiden och eliminerar helt steady state -felet. Det ökar dock toppöverskottet och avvecklingstiden.

• Stämning: Ett bra styrsystem har låg stigningstid, avvecklingstid, toppöverskridning och steady state -fel. Därför måste Kp, Kd, Ki finjusteras för att justera bidraget från ovanstående faktorer för att få ett bra kontrollsystem.

Figur har bifogats som visar effekten av att ändra olika parametrar i PID -algoritmen.

Steg 3: Självbalanseringsrobot

En självbalanserande robot är en tvåskiktsrobot med flera lager.

Roboten kommer att försöka balansera sig själv med tillämpning av ojämn kraft. Det kommer att balansera sig själv genom att använda kraft som motsätter sig resultatet av krafterna på roboten.

Metoder för självbalansering

Det finns fyra metoder för självbalansering av robotar. Dessa är följande:

Självbalansering med två IR -lutningssensorer

Detta är ett av de grövsta sätten att balansera roboten eftersom den kräver mycket mindre hårdvara och en relativt enkel algoritm. I detta tillvägagångssätt används två lutande IR -sensorer för att mäta avståndet mellan marken och roboten. Baserat på det beräknade avståndet kan PID användas för att driva motorerna för att balansera roboten i enlighet därmed. En nackdel med denna metod är att IR -sensorn kan missa några avläsningar. Ett annat problem är att ett avbrott och slingor krävs för beräkning av avstånd som ökar algoritmens tidskomplexitet. Därför är denna metod för att balansera roboten inte mycket effektiv.

Självbalansering med accelerometer

Accelerometer ger oss kroppens acceleration i 3 axlar. Acceleration orienterad i y-axeln (uppåt) och x-axeln (framåt) ger oss måttet för att beräkna gravitationens riktning och därmed beräkna lutningsvinkeln. Vinkeln beräknas enligt följande:

θ = arctan (Ay/Ax) (1.2)

Nackdelen med att använda denna metod är att under robotens rörelse kommer den horisontella accelerationen också att läggas till avläsningarna som är ett högfrekvent brus. Därför blir lutningsvinkeln felaktig.

Självbalansering med hjälp av gyroskop

Ett gyroskop används för att beräkna vinkelhastigheterna längs de tre axlarna. Lutningsvinkeln erhålls med följande ekvation.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

En stor nackdel med att använda gyroskopet är att det har en liten DC Bias som är ett lågfrekvent brus och på några få gånger är de returnerade värdena helt felaktiga. Detta, efter integration, kommer att få nollpunkten att försvinna. Som ett resultat av det kommer roboten att förbli i sitt vertikala läge under en tid och falla omkull när driften kommer.

Självbalansering med både accelerometer och gyroskop

Som diskuterats ovan kommer det inte att ge oss rätt lutningsvinkel om du bara använder accelerometer eller gyroskop. För att redogöra för det används både accelerometer och gyroskop. Dessa är båda inbäddade i MPU6050. I detta hämtar vi data från dem båda och smälter dem sedan antingen med hjälp av Kalman -filter eller kompletterande filter.

• Kalman -filter: Kalman -filtret beräknar den bästa uppskattningen av tillståndet för ett dynamiskt system från bullriga mätningar, vilket minimerar uppskattningens genomsnittliga kvadratfel. Det fungerar i två steg, förutsägelse och korrigering, med tanke på de diskreta stokastiska ekvationerna som beskriver systemdynamiken. Det är emellertid en mycket komplex algoritm att implementera särskilt på en begränsad hårdvara hos en mikrokontroller.

• Kompletterande filter: Denna algoritm använder främst data som erhållits från gyroskopet och integrerar det över tid för att få lutningsvinkeln. Den använder också en liten andel av accelerometeravläsningar. Kompletterande filter minimerar faktiskt accelerationsmätarens högfrekventa brus och gyroskopets lågfrekventa brus och säkrar dem sedan för att ge den bästa exakta lutningsvinkeln.

Steg 4: Design av robot

Vi har designat en självbalanserande robot som använder Proportional Derivative controller implementerad av kompletterande filter för MPU6050. Denna lilla modell av Self Balancing Robot kommer att illustrera användbarheten av styrsystem i självbalansering av robotar.

System implementering:

Systemet är en självbalanserande robot. Det implementeras med hjälp av PID Controller som är en proportionell integrerad derivatkontroller. Vi balanserar roboten genom att köra hjulen i fallets riktning. Genom att göra det försöker vi hålla robotens tyngdpunkt ovanför svängpunkten. För att driva hjulen i fallets riktning bör vi veta var roboten faller och med vilken hastighet den faller. Dessa data erhålls med MPU6050 som har en accelerometer och ett gyroskop. MPU6050 mäter lutningsvinkeln och ger sin effekt till mikrokontrollen. MPU6050 är anslutet till STM -kortet genom I2C. I I2C är en tråd för klockan som heter SCL. Den andra är för dataöverföringen som är SDA. I detta används master -slavkommunikation. Startadress och slutadress anges för att veta varifrån data börjar och var de slutar. Vi har implementerat kompletteringsfiltret här för MPU6050 som är ett mattefilter för att slå samman utgångarna från accelerometer och gyroskop. Efter att ha fått data från MPU6050 kommer mikrokontrollern att utföra beräkningar för att veta var den faller. Baserat på beräkningarna kommer STM-mikrostyrenheten att ge kommandon till motorföraren för att köra fordonen i fallande riktning, vilket kommer att balansera roboten.

Steg 5: Projektkomponenter

Följande komponenter användes i självbalanseringsrobotprojektet:

STM32F407

En mikrokontroller designad av ST Microelectronics. Det fungerar på ARM Cortex-M Architecture.

Motorförare L298N

Denna IC används för att köra motorn. Den får två externa ingångar. En från mikrokontrollern som ger den en PWM -signal. Genom att justera bredden på pulsen kan motorhastigheten justeras. Dess andra ingång är den spänningskälla som krävs för att driva motorn, vilket är ett 12V batteri i vårt fall.

DC -motor

En likströmsmotor går på likström. I detta experiment kör DC -motorn med optokopplare anslutna till motorföraren. För att driva motorn har vi använt Motor Drive L298N.

MPU6050

MPU6050 används för att få information om var roboten faller. Den mäter lutningsvinkeln i förhållande till nolllutningspunkten som är positionen för MPU6050 när programmet börjar köras.

MPU6050 har en 3-axlig accelerometer och ett 3-axligt gyroskop. Acceleratorn mäter acceleration längs de tre axlarna och gyroskopet mäter vinkelhastigheten kring de tre axlarna. För att kombinera utmatningen måste vi filtrera ut ljuden från båda. För att få bort ljuden har vi Kalman och kompletterande filter. Vi har implementerat kompletteringsfilter i vårt projekt.

Opto Par 4N35

En optokopplare är en enhet som används för att isolera lågspänningsdelen och högspänningsdelen av kretsen. Som namnet antyder fungerar det utifrån ljus. När lågspänningsdelen får en signal kommer strömflöden i högspänningsdelen

Steg 6: Robotens struktur

Robotens struktur förklaras enligt följande:

Fysisk struktur

Självbalanseringsroboten består av två lager av transparent plastglas. Detaljerna för två lager ges nedan:

Första lagret

I den nedre delen av första lagret har vi placerat en cell för att driva STM -kortet. Två motorer på 4 volt vardera har placerats på varje sida med däck anslutna för att roboten ska kunna röra sig. I den övre delen av det första lagret har två batterier på 4 volt vardera (totalt 8 volt) och motorföraren IC (L298N) placerats för drift av motorer.

Andra lagret

I robotens övre lager har vi placerat STM -kortet på Perf Board. Ytterligare en perf kartong med 4 optokopplare placeras på det översta lagret. Gyroskop placeras också på robotens översta lager från undersidan. Båda komponenterna placeras i mitten så att tyngdpunkten hålls så låg som möjligt.

Robotens tyngdpunkt

Tyngdpunkten hålls så låg som möjligt. För detta ändamål har vi placerat tunga batterier på bottenlagret och lätta komponenter som STM -kort och optokopplare på det övre lagret.

Steg 7: Kod

Koden sammanställdes på Atollic TrueStudio. STM studio användes för felsökningsändamål.

Steg 8: Slutsats

Efter mycket experimenterande och observation har vi äntligen kommit till den punkt där vi sammanfattar våra resultat och diskuterar hur långt vi lyckades genomföra och utarbeta systemets effektivitet.

Allmän översyn

Under experimentet kontrollerades motorns hastighet framgångsrikt med hjälp av PID -algoritmen. Kurvan är dock inte exakt en jämn rak linje. Det finns många anledningar till det:

• Sensorn är visserligen ansluten till ett lågpassfilter och tillhandahåller fortfarande vissa ändliga avstängningar; dessa beror på de olinjära motstånden och några oundvikliga skäl för den analoga elektroniken.

• Motorn roterar inte smidigt under liten spänning eller PWM. Det ger ryck som kan orsaka felaktiga värden som matas till systemet.

• På grund av vinglar kan sensorn missa vissa slitsar som ger högre värden. • En annan stor orsak till fel kan vara kärnklockfrekvensen för STM micrcontroller. Denna modell av STM mikrokontroller ger en kärna på 168MHz. Även om detta problem behandlas i detta projekt, finns det en övergripande uppfattning om denna modell att den inte exakt ger så hög frekvens.

Open loop -hastigheten ger en mycket smidig linje med bara några oväntade värden. PID -algoritmen fungerar också bra och ger en mycket låg avvecklingstid för motorn. Motorns PID -algoritm testades under olika spänningar som höll referenshastigheten konstant. Spänningsändringen ändrar inte motorns varvtal som visar att PID -algoritmen fungerar fint

Effektivitet

Här diskuterar vi effektiviteten hos PID -regulatorn som vi observerade under experimentet.

Enkel implementering

Vi har sett i experiment- och observationsavsnittet att en PID -styrenhet är mycket lätt att implementera. Det kräver bara tre parametrar eller konstanter som måste ställas in för att ha ett hastighetskontrollsystem

Oöverträffad effektivitet för linjära system

Linjär PID -styrenhet är den mest effektiva i familjen av styrenheter eftersom logiken är mycket enkel och applikationen är utbredd vid linjära eller ganska linjära applikationer.

Begränsningar

Vi förklarade abstrakt om systemets begränsningar. Här diskuterar vi några av dem som vi observerade.

Urval av konstanter

Vi har sett att även om en PID -styrenhet är lätt att implementera, är det ändå en stor nackdel med systemet att steget med att välja värdet på konstanter är ett mödosamt steg. som man måste göra svåra beräkningar. Det andra sättet är hit and trial -metoden, men det är inte heller effektivt.

Konstanter är inte alltid konstanta

De experimentella resultaten visade att för olika värden på referenshastigheten för motorn fungerade PID -regulatorn felaktigt för samma värden för PID -konstanterna. För olika hastigheter måste konstanterna väljas olika och detta ökar beräkningskostnaden exponentiellt.

Icke linjärt

PID -regulatorn som används i vårt fall är linjär, därför kan den endast tillämpas på linjära system. För icke-linjära system måste regulatorn implementeras olika. Även om olika icke -linjära metoder för PID är tillgängliga kräver de att fler parametrar väljs. Detta gör igen systemet oönskat på grund av höga beräkningskostnader.

Initial Push krävs

Vi visade i experimentavsnittet att för en ganska liten referenshastighet där felet är ganska litet i starten, är PWM som tillhandahålls av PID så liten att den inte genererar det nödvändiga startmomentet för motorn. Så motorn går i vissa försök inte eller i andra försök ger en stor överskridande och en längre avvecklingstid.

Steg 9: Särskilt tack

Ett särskilt tack till mina gruppmedlemmar som hjälpte mig genom detta projekt.

Jag laddar upp länken till videon snart.

Jag hoppas att du tycker att det här är intressant.

Detta är Tahir Ul Haq från UET som loggar ut. Skål !!!