CNC -trumplotter: 13 steg (med bilder)

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:44

Denna instruktion beskriver en A4/A3-plotter tillverkad av en sektion av plaströr, två BYJ-48-stegmotorer och en SG-90-servo. I huvudsak är det en plattbäddsplotter som rullas ihop till en trumma.

En motor roterar trumman medan den andra flyttar skrivhuvudet. Servon används för att höja och sänka pennan.

Denna plotter har ett antal fördelar jämfört med en traditionell flatbottenplotter:

• betydligt mindre fotavtryck
• kräver bara en linjär styrskena
• enkel att konstruera
• billig

En inbyggd tolk accepterar gcode-utmatningen från Inkscape.

Kommunikation med plotteren sker via en bluetooth -länk.

Plotteren är kompatibel med CNC-grafikkortet som beskrivs i min instruerbara

Även om det inte är ett precisionsinstrument, är noggrannheten hos denna plotter tillfredsställande för det avsedda syftet att överföra akvarellkonturer till papper.

Steg 1: Kretsen

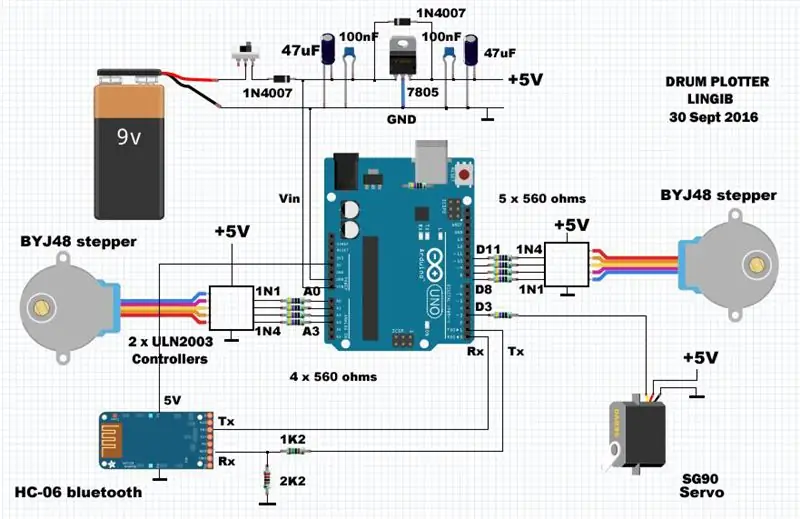
Kretsen består av en Arduino UNO R3 mikrokontroller och en anpassad skärm som de diskreta komponenterna är monterade på. Strömförsörjning sker via en extern 5 volt 1 amp regulator. Den genomsnittliga strömmen är cirka 500mA.

Stegmotorerna BYJ-48 är anslutna till PORTB (stift D8, D9, D10, D11) och PORTC (stift A0, A1, A2, A3). SG-90 pennlyftservo är fäst på stift D3.

Motstånden på 560 ohm, som kan utelämnas, ger ett mått på kortslutningsskydd för arduino om något skulle gå fel. De gör det också lättare att sätta på skärmen eftersom de fungerar som "hoppare" över tillförselskenorna.

Motstånden 1k2 och 2K2 förhindrar skador på HC-06 bluetooth-modulen [1] genom att sänka 5 volt-utgången från arduino ner till 3,3 volt.

[1] Koppla ur HC-06 bluetooth-modulen när du laddar upp kod till arduino via USB-porten. Detta undviker eventuella seriella portkonflikter.

Steg 2: Linjär enhet

Den linjära drivningen är gjord av en längd av 3 mm x 32 mm aluminiumstång, en remsa av aluminiumplåt och fyra små kullagerhjul.

Aluminiumet är tillgängligt från de flesta järnaffärer. U624ZZ 4x13x7mm U-spårskivor finns på

Enkla handverktyg är allt du behöver. Skär aluminiumstången så att den passar dina plottermått.

Motoraggregatet

Montera BJY-48 stegmotor genom stången i ena änden och fäst en GT2 20 tand, 5 mm borrning, remskiva till motoraxeln. Montera nu ytterligare en GT2 -remskiva i andra änden av din stång så att remskivan kan rotera fritt. Jag använde en 5 mm diameter rörformad (radio) distans och en 3 mm bult för att uppnå detta.

Slinga nu en längd med GT2 -kuggrem runt remskivorna. Anslut kuggremens ändar med hjälp av en halvvridning så att tänderna flätar ihop och fixerar med ett buntband.

Slutligen fäst vagnenheten på kuggremmen med ett buntband.

Vagnenheten

Vagnenheten är tillverkad av en remsa av aluminiumplåt [1] på vilken U624ZZ -remskivorna är bultade. Använd vid behov en bricka på 4 mm för att placera remskivorna från aluminiumplåten.

Remskivorna, som har ett 4 mm spår, sträcker sig över aluminiumstångens topp och botten så att det inte finns någon vertikal rörelse men aluminiumremsan rör sig fritt åt vänster och höger.

För att säkerställa att vagnen går fritt, monterar du först de två översta remskivorna och markerar positionerna för de två nedre remskivorna med remskivorna sittande på stången. Hålen för dessa två remskivor kan nu borras. Använd först en liten "pilot" -borr för att förhindra att den större 4 mm -borren driver.

Innan du böjer aluminiumremsan till ett "U", borra ett hål upptill och nedtill så att det passar din penndiameter. Slutför nu böjarna.

Fäst kuggremmen på vagnen med hjälp av ett buntband och en 3 mm bult mellan de två översta remskivorna.

Pennlyftaggregatet

Fäst en SG-90-servo på ovansidan av vagnen med en eller två buntband.

Släpp ner pennan i de två hålen du har borrat. Se till att pennan glider upp och ner fritt.

Fäst en "krage" på din penna så att pennan är helt fri från trumman när servon är i pennläget.

[1] Aluminium kan skäras genom att göra båda sidorna av arket med en vass kniv (box-cutter) och sedan böja snittet över kanten på ett bord. Några vickor och arket kommer att spricka och lämna en rak paus. Till skillnad från tenn-snips knäcker denna metod inte aluminiumet.

Steg 3: Trumman

Trumman består av en sektion av plaströr med två träändproppar [1].

Använd en kompass, inställd på rörets inre radie, för att rita ändpluggens konturer. Skär nu runt varje kontur med en fin bladsåg ("coping", "fret") och anpassa sedan varje ändplugg med hjälp av en trärasp. Fäst ändpluggarna med små, nedsänkta träskruvar.

En 6 mm konstruktionsbult genom mitten av varje ändpropp bildar axeln.

Trummått

Trummåtten bestäms av din pappersstorlek. En trumdiameter på 100 mm stöder A4 porträtt och A3 liggande. En trumdiameter på 80 mm stöder endast liggande A4. Använd så liten trumldiameter som möjligt för att minska trögheten … BYJ-48-motorerna är bara små.

En trumdiameter på 90 mm är idealisk för A4 -porträtt- och A3 -liggande papper eftersom de motsatta kanterna, när de lindas runt trumman, överlappar cirka 10 mm vilket innebär att du bara har en söm att tejpa på plats.

Rotera trumman

Varje axel passerar genom en aluminiumändfäste så att trumman kan rotera fritt. Ändflottan förhindras med hjälp av en GT-2, 20 tand, 6 mm borrning, remskiva fäst vid axeln i ena änden. Ett kontinuerligt GT-2-kuggrem binder länkad BJY-48-stegmotor till trumman. Motorn kräver en remskiva med en borrstorlek på 5 mm.

[1] Plaständproppar finns för de flesta rördiametrar men avvisades eftersom de passade över röret snarare än inuti och plasten tenderar att böja. De skulle förmodligen vara okej om en kontinuerlig axel användes istället för bultarna … men då krävs en metod för att fästa axeln på ändpluggarna.

Steg 4: Konstruktionstips

Se till att pennan går längs trummans mitt. Detta kan uppnås genom att skära hörnen ur trästöden. Om pennan står utanför mitten tenderar den att glida nedåt på trumman.

Noggrann borrning av de två pennhålen är viktig. Eventuella vinglar i pennledaren eller vagnenheten kommer att orsaka vinglar längs X-axeln.

Dra inte åt GT-2-tandremmen för hårt … de behöver bara vara spända. BYJ-48 stegmotorer har inte mycket vridmoment.

BJY-48 stegmotorer uppvisar ofta små mängder av backlash vilket är obetydligt längs X-axeln men är oroande när det gäller Y-axeln. Anledningen till detta är att en rotation av Y-axelmotorn motsvarar en rotation av trumman, medan pennvagnen kräver många varv på X-axelmotorn för att korsa trummans längd. Varje Y-axel motreaktion kan elimineras genom att hålla ett konstant vridmoment på trumman. En enkel metod är att fästa en liten vikt på en nylonsladd som lindas runt trumman.

Steg 5: Bresenhams ritritningsalgoritm

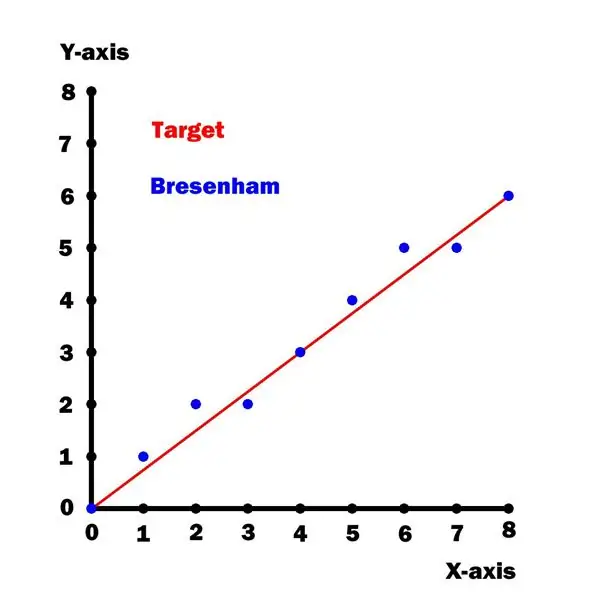
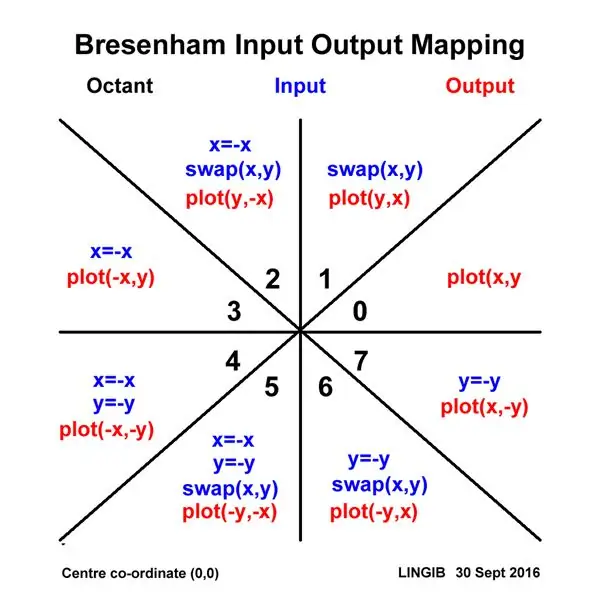
Denna plotter använder en optimerad version [1] av Bresenhams ritritningsalgoritm. Tyvärr gäller denna algoritm endast för linjebackningar som är mindre än eller lika med 45 grader (dvs en oktant av en cirkel).

För att komma runt denna begränsning "kartlägger" jag alla XY -ingångar till den första "oktanten", sedan "tar jag bort dem" när det är dags att plotta. In- och utmatningsfunktionerna för att uppnå detta visas i diagrammet ovan.

Härledning

Resten av detta steg kan utelämnas om du är bekant med Bresenhams algoritm.

Låt oss dra en linje från (0, 0) till (x1, y1) där:

• x1 = 8 = horisontellt avstånd
• y1 = 6 = vertikalt avstånd

Ekvationen för en rak linje som passerar genom ursprunget (0, 0) ges av ekvationen y = m*x där:

m = y1/x1 = 6/8 = 0,75 = lutning

Enkel algoritm

En enkel algoritm för att rita denna linje är:

• int x1 = 8;
• int y1 = 6;
• flyta m = y1/x1;
• plot (0, 0);
• för (int x = 1; x <= x1; x ++) {
• int y = rund (m*x);
• plot (x, y);
• }

Tabell 1: Enkel algoritm

x	m	m*x	y
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Det finns två problem med denna enkla algoritm:

• huvudslingan innehåller en multiplikation som är långsam
• den använder flyttal som också är långsam

Ett diagram över y mot x för denna rad visas ovan.

Bresenhams algoritm

Bresenham introducerade begreppet en felbegrepp 'e' som initialiseras till noll. Han insåg att m*x -värdena som visas i tabell 1 kan erhållas genom successiv tillsats av 'm' till 'e'. Han insåg vidare att y bara ökas om bråkdelen av m*x är större än 0,5. För att hålla sin jämförelse inom intervallet 0 <= 0,5 <= 1 subtraherar han 1 från 'e' när y ökas.

• int x1 = 8;
• int y1 = 6;
• flyta m = y1/x1;
• int y = 0;
• float e = 0;
• plot (0, 0);
• för (int x = 1; x <= x1; x ++) {
• e+= m;
• om (e> = 0,5) {
• e -= 1;
• y ++;
• }
• plot (x, y);
• }

Tabell 2: Bresenhams algoritm

x	m	e	e-1	y
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Om du undersöker algoritmen och tabell 2 kommer du att observera att;

• huvudslingan använder bara addition och subtraktion … det finns ingen multiplikation
• mönstret för y är detsamma som för tabell 1.

Men vi använder fortfarande flyttal … låt oss fixa detta.

Bresenhams (optimerade) algoritm

Bresenhams flytande punktalgoritm kan konverteras till ett heltal om vi skalar 'm' och 'e' med 2*x1 i vilket fall m = (y1/x1)*2*x1 = 2*y1

Bortsett från skalning 'm' och 'e' är algoritmen liknande den ovan utom:

• vi lägger till 2*y1 till 'e' varje gång vi ökar 'x'
• vi ökar y om e är lika med eller större än x1.
• vi subtraherar 2*x1 från 'e' istället för 1
• x1 används för jämförelsen istället för 0,5

Algoritmens hastighet kan ökas ytterligare om slingan använder noll för testet. För att göra detta måste vi lägga till en förskjutning till feltermen 'e'.

• int x1 = 8;
• int y1 = 6;
• int m = (y1 << 1); // konstant: lutning skalad med 2*x1
• int E = (x1 << 1); // konstant: 2*x1 för användning i loop
• int e = -x1; // offset av -E/2: testet nu gjort på noll
• plot (0, 0);
• int y = 0;
• för (x = 1; x <= x1; x ++) {
• e += m;
• om (e> = x1) {
• e -= E
• y ++;
• }
• plot (x, y);
• }

Tabell 3: Bresenhams (optimerade) algoritm

x	m	E	e	e - E	y
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Återigen är mönstret för y detsamma som i de andra tabellerna. Det är intressant att notera att tabell 3 endast innehåller heltal och att förhållandet m/E = 12/16 = 0,75 som är linjens lutning 'm'.

Denna algoritm är extremt snabb eftersom huvudslingan endast innebär addition, subtraktion och en jämförelse med noll. Multiplikation används inte förutom när vi initierar värdena för 'E' och 'm' med hjälp av ett "vänster-skift" för att fördubbla värdena för x1 och y1.

[1] Denna optimerade version av Bresenhams algoritm är från ett papper "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Hans material kan användas för ideell forskning och utbildning, förutsatt att du krediterar honom och länkar tillbaka till hans hemsida,

Steg 6: Koden

Ladda ner den bifogade filen till en mapp med samma namn och ladda upp den till plotteren med din arduino IDE (integrerad utvecklingsmiljö).

Koppla ur HC-06 bluetoorh-modulen innan du försöker ladda upp. Detta är nödvändigt för att undvika en seriell portkonflikt med USB -kabeln.

Tredjepartskod

Förutom ovanstående.ino-kod behöver du följande programvarupaket som är gratis / donations-ware:

• Teraterm som är tillgängligt från
• Inkscape som är tillgängligt från

Instruktioner för installation och användning av vart och ett av ovanstående paket från tredje part finns i min artikel

Steg 7: Meny

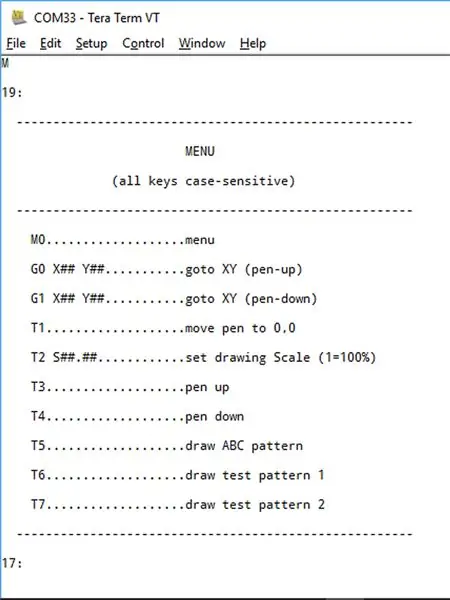
Gör en bluetooth -anslutning med din plotter med "Teraterm".

Slå på "caps lock" eftersom alla kommandon är versaler.

Skriv bokstaven 'M' och en meny ska visas som visas ovan.

Menyn är rimligen självförklarande:

• M (eller M0) visar menyn
• Med G0 kan du skicka pennan till en specifik XY-koordinat med pennan upphöjd.
• Med G1 kan du skicka pennan till en specifik XY-koordinat med pennan sänkt.
• T1 låter dig placera din penna över din 0, 0-koordinat. Skriv "E" för att avsluta.
• T2 låter dig skala din ritning. Till exempel "T2 S2.5" skalar din ritning till 250%. Standardskalan är 100%
• Med T3 och T4 kan du höja eller sänka pennan.
• T5 ritar ett "ABC" testmönster.
• T6 ritar ett "mål".
• T7 ritar en rad radiella linjer, vars syfte är att verifiera att Bresenhams algoritm fungerar i var och en av de åtta "oktanterna"

Anmärkningar:

• alla pennrörelser använder ritningsskala med menyalternativet T2
• "17:" - och "19:" -numren är "Xon" och "Xoff" terminalhandskodskoderna från arduino -tolken.

Steg 8: Kalibrering

Värdena för X_STEPS_PER_MM och Y_STEPS_PER_MM är för en trumma med en diameter på 90 mm.

Värden för andra trumdiametrar kan beräknas med hjälp av följande samband:

• trummans omkrets är PI*diameter
• 2048 steg motsvarar ett varv för varje motoraxel
• ett varv av en GT-2 remskiva motsvarar 40 millimeter linjär rörelse hos ett kuggrem

En annan metod är att ange följande kommandon,

• G1 X0 Y100
• G1 X100 Y100

mät sedan längden på de resulterande raderna och "skala" värdena för X-STEPS_PER_MM och Y_STEPS_PER_MM

Steg 9: Gcode -förbehandling

Denna plotter kräver bara fyra av Inkscape gcodes (nämligen G0, G1, G2, G3). Koden körs betydligt snabbare om vi tar bort alla onödiga gkoder och kommentarer.

För att göra detta behöver du en kopia av "Notepad ++". Denna fritextredigerare innehåller en sökmotor med "vanligt uttryck" för att hitta och ta bort oönskad text. Anteckningar ++ är tillgängliga från

Öppna filen som ska ändras med Anteckningar ++ och placera markören högst upp i filen.

Välj "Visa/Visa symbol/Alla tecken" följt av "Sök/Ersätt …" från den översta menyraden.

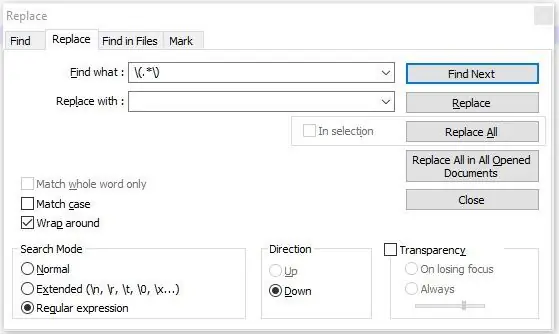
Klicka på kryssrutan "Regular Expression" (se första bilden) och ange var och en av följande kodsekvenser i sökrutan.

Klicka på "Ersätt alla" efter varje post:

• %
• (.*)
• ^M.*$
• Z.*$

Ovanstående regeluttryck tar bort alla % -symboler, alla kommentarer som visas inom parentes, alla M -koder, alla Z -koder och koder som följer.

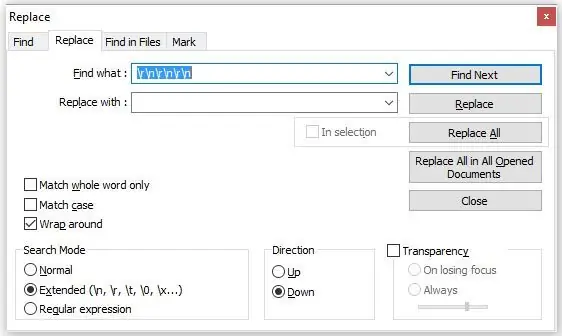
Klicka nu på kryssrutan "Utökat uttryck" (se andra bilden) och ange följande kodsekvens:

r / n / r / n / r / n

Detta uttryck tar bort oönskade vagnreturer och radmatningar som skapats av den första sekvensen.

Spara filen under ett annat namn med "Spara som".

Gjort.

Steg 10: Resultat

Denna plotter byggdes som "proof of concept" och var aldrig avsedd att vara perfekt. Med det sagt att resultaten inte är så dåliga. De uppfyller definitivt mitt designmål att överföra akvarellkonturer på papper.

De tre första bilderna är de inbyggda testmönstren T5, T6, T7 respektive.

"Hej världen!" mönstret skickades till plotteren via bluetooth. En "förbehandlad" kopia av den här filen bifogas.

Steg 11: Koduppdatering

Koden för denna plotter har uppdaterats till Drum_Plotter_V2.ino.

Ändringar från den ursprungliga Drum_Plotter.ino inkluderar:

• mjukare pennpositionering
• känner igen G02 gcode -instruktioner (medurs bågar)
• känner igen G03 gcode-instruktioner (moturs)

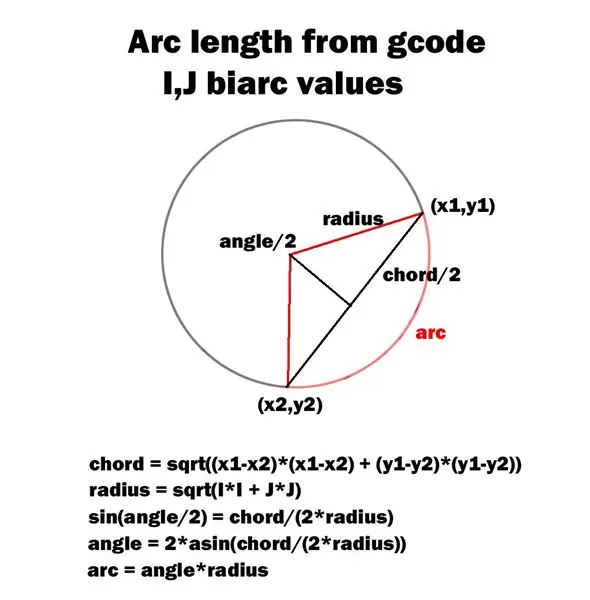
Det bifogade diagrammet beskriver min metod för att beräkna bågvinkeln.

Steg 12: Drum_plotter_v3.ino

En koduppdatering för "CNC Drum Plotter" är bifogad.

"drum_plotter_v3.ino" åtgärdar ett mindre fel som påverkade plotterns noggrannhet.

Förändra historien

Version 2:

Bi-bågskurvor tillagda

Version 3:

Följande funktioner skrevs om för att åtgärda en mindre bugg som påverkade plotterns noggrannhet.

• (int) ersatt med runda () i funktionen move_to ().
• draw_line () funktion "oktant" sökalgoritm förbättrad
• Tolkaren använder nu strängfunktioner snarare än pekare vilket förenklar designen. Till exempel kan vi nu söka efter "MENY" istället för att leta efter bokstaven "M" och extrahera det heltal som följer. Detta gör att du kan anpassa plotteren med dina egna kommandon.

Steg 13: Drum_plotter_plotter_v4.ino

16 januari 2017:

Koden för denna trumplotter har optimerats ytterligare. Ytterligare funktioner har lagts till.

Ändringarna inkluderar:

• snabbare draw_line () algoritm
• matchande move_to () -funktion
• stegräknare
• mindre buggfix

För ytterligare information läs kommentarerna i "drum_plotter_v4.ino" bifogade.

Klicka här för att se mina andra instruktioner.