Innehållsförteckning:
- Tillbehör
- Steg 1: Ladda ner de nödvändiga filerna
- Steg 2: Hur man öppnar och spelar Python Othello
- Steg 3: Minimax -algoritm: Generera scenarier
- Steg 4: Minimax: Utvärderingskortkonfigurationer
- Steg 5: Minimax -algoritm: Välja bästa drag
- Steg 6: Minimax -algoritm: Pseudokod
- Steg 7: Gör din AI med Ai_template.py
- Steg 8: Dags att få AI att slåss
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:44.
- Senast ändrad 2025-01-23 15:11.



Har du någonsin undrat hur de datorer du spelar mot i schack eller pjäser är gjorda? Tja, leta inte längre än denna Instructable för den kommer att visa dig hur du gör en enkel men effektiv artificiell intelligens (AI) med hjälp av Minimax -algoritmen! Genom att använda Minimax -algoritmen gör AI välplanerade och genomtänkta drag (eller åtminstone efterliknar en tankeprocess). Nu kan jag bara ge dig koden för AI som jag gjorde, men det skulle inte vara kul. Jag ska förklara logiken bakom datorns val.
I denna instruktionsbok går jag igenom stegen om hur du gör en AI för Othello (AKA Reversi) i python. Du bör ha en mellanliggande förståelse för hur du kodar i python innan du tacklar detta projekt. Här är några bra webbplatser att titta på för att förbereda dig för denna instruerbara: w3schools eller learnpython. I slutet av denna instruerbara, bör du ha en AI som kommer att göra beräknade drag och bör kunna besegra de flesta människor.
Eftersom denna Instructable främst kommer att handla om hur man gör en AI kommer jag inte att förklara hur man designar ett spel i python. Istället kommer jag att ge koden för spelet där en människa kan spela mot en annan människa och ändra den så att du kan spela ett spel där en människa spelar mot AI.
Jag lärde mig att skapa denna AI genom ett sommarprogram på Columbia SHAPE. Jag hade det bra där så ta en titt på deras hemsida för att se om du skulle vara intresserad.
Nu när vi fått logistiken ur vägen, låt oss börja koda!
(Jag satte ett par anteckningar i bilderna så se till att titta på dem)
Tillbehör
Det här är lätt:
1) Dator med en pythonmiljö som Spyder eller IDLE
2) Ladda ner filerna för Othello -spelet från min GitHub
3) Din hjärna med tålamod installerat
Steg 1: Ladda ner de nödvändiga filerna


När du går in i min GitHub ska du se 5 filer. Ladda ner alla 5 och placera dem alla i samma mapp. Innan vi kör spelet, öppna alla filer i spyder -miljön.
Så här gör filerna:
1) othello_gui.py denna fil skapar spelbrädet för spelarna att spela på (oavsett om det är mänskligt eller dator)
2) othello_game.py den här filen spelar två datorer mot varandra utan spelbordet och visar bara poäng och flyttpositioner
3) ai_template.py det är här du kommer att lägga all din kod för att göra din AI
4) randy_ai.py detta är en förgjord AI som väljer sina drag slumpmässigt
5) othello_shared.py ett gäng färdiga funktioner som du kan använda för att göra din AI så som att kontrollera om det finns tillgängliga drag, poängen eller styrelsen
6) De tre andra filerna: Puma.py, erika_5.py och nathan.py, gjorda av mig, Erika respektive Nathan från SHAPE -programmet, dessa är tre olika AI med unika koder
Steg 2: Hur man öppnar och spelar Python Othello


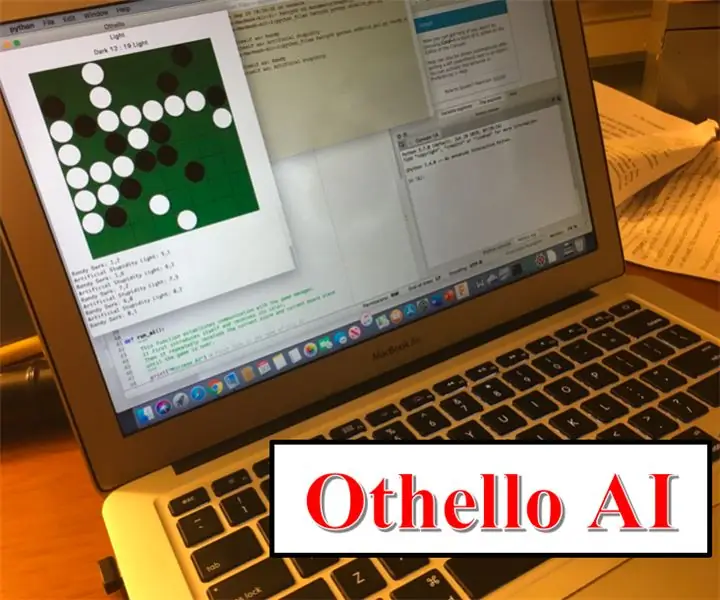
När du har alla filer öppna skriver du "kör othello_gui.py" i det nedre högra hörnet av skärmen och trycker på enter i IPython-konsolen. Eller i Mac -terminalen skriver du "python othello_gui.py" (när du är i rätt mapp förstås). Då borde en tavla dyka upp på din skärm. Detta läge är det mänskliga vs mänskliga läget. Ljuset går andra och mörker först. Titta på min video om du är förvirrad. iHögst upp finns poängen för varje färgplatta. För att spela, klicka på ett giltigt flyttutrymme för att placera en bricka där och ge sedan datorn till din motståndare som kommer att göra detsamma och upprepa.
Om du inte vet hur du spelar Othello, läs dessa regler från ultra boards webbplats:
Svart rör sig alltid först. Ett drag görs genom att placera en skiva med spelarens färg på brädet i en position som "out-flanks" en eller flera av motståndarens skivor. En skiva eller rad med skivor flankeras när den omges i ändarna av skivor med motsatt färg. En skiva kan flankera ett antal skivor i en eller flera rader i valfri riktning (horisontellt, vertikalt, diagonalt)…. (läs färdigt på deras hemsida)
Skillnaden mellan det ursprungliga spelet och detta pythonspel är att när det inte finns några giltiga drag kvar för en spelare slutar spelet
Nu när du kan spela spelet med en vän, låt oss göra en AI som du kan spela med.
Steg 3: Minimax -algoritm: Generera scenarier

Innan vi pratar om hur man skriver detta i kod, låt oss gå igenom logiken bakom det. Minimax-algoritmen är en beslutsfattande, back-tracking-algoritm och används vanligtvis i turbaserade spel med två spelare. Målet med denna AI är att hitta nästa bästa drag och följande bästa drag tills det vinner spelet.
Hur skulle algoritmen avgöra vilket drag som är det bästa draget? Stanna upp och tänk på hur du skulle välja nästa drag. De flesta skulle välja det drag som skulle ge dem flest poäng, eller hur? Eller om de tänkte framåt, skulle de välja det drag som skulle skapa en situation där de kunde få ännu fler poäng. Det senare tankesättet är hur Minimax -algoritmen tänker. Det ser framåt till alla framtida styrelsens inställningar och gör det drag som skulle leda till flest poäng.
Jag kallade detta en backtracking -algoritm, eftersom den börjar med att först skapa och utvärdera alla framtida styrelsestater med tillhörande värden. Detta innebär att algoritmen kommer att spela spelet så många som det behöver (göra rörelserna för sig själv och motståndaren) tills varje scenario i spelet har spelats. För att hålla reda på alla tavlor (scenarier) kan vi rita ett träd (titta på bilderna). Trädet på bilden ovan är ett enkelt exempel på ett spel med Connect 4. Varje brädkonfiguration kallas en styrelse och dess plats på trädet kallas en nod. Alla noder längst ner i trädet är de sista brädstaterna efter att ha gjort alla drag. Uppenbarligen är vissa styrelsestater bättre för en spelare än den andra. Så nu måste vi få AI att välja vilken styrelsestat den vill komma till.
Steg 4: Minimax: Utvärderingskortkonfigurationer


För att ge värden till brädstaterna måste vi lära oss strategierna för spelet som vi spelar: i detta fall Othellos strategier. Eftersom det här spelet är en kamp för att vända motståndarens och dina skivor, är de bästa skivpositionerna de som är stabila och inte kan vändas. Hörnet, till exempel, är den plats där när en skiva placeras kan den inte ändras till den andra färgen. Således skulle den platsen vara extremt värdefull. Andra bra positioner inkluderar sidorna på brädet som gör att du kan ta många stenar. Det finns fler strategier på denna webbplats.
Nu kan vi tilldela värden till positionerna för varje styrelsestatstyrelse. När en position är upptagen av AI: s del ger du ett visst antal poäng beroende på positionen. Till exempel, på en tavla där AI: s bit är i hörnet, kan du ge en bonus på 50 poäng, men om det var på en ogynnsam plats kan stycket ha ett värde på 0. Efter att ha tagit hänsyn till alla värden på positionerna tilldelar du styrelsen ett värde. Till exempel, om AI har en bit i hörnet kan styrelsestaten ha en poäng på 50 medan en annan styrelse med AI: s bit i mitten har en poäng på 10.
Det finns många sätt att göra detta, och jag har tre olika heuristik för att utvärdera bräddelarna. Jag uppmuntrar dig att göra din egen typ av heurist. Jag laddade upp tre olika AI: er till min github av tre olika tillverkare, med tre olika heuristik: Puma.py, erika5.py, nathanh.py.
Steg 5: Minimax -algoritm: Välja bästa drag




Nu skulle det vara trevligt om AI bara kunde välja alla drag för att komma till styrelsen med den högsta poängen. Men kom ihåg att AI också valde drag för motståndaren när den genererade alla brädstaterna och om motståndaren är smart, tillåter den inte AI att nå det högsta brädpoänget. Istället skulle en smart motståndare ta steget för att få AI att gå till lägsta styrelsestat. I algoritmen kallar vi de två spelarna för en maximeringsspelare och en minimiserande spelare. AI skulle vara den maximerande spelaren eftersom den vill få flest poäng för sig själv. Motståndaren skulle vara den minimiserande spelaren eftersom motståndaren försöker göra flytten där AI får minst poäng.
När alla kortstaterna har genererats och värden har tilldelats korten börjar algoritmen att jämföra korttillstånden. På bilderna skapade jag ett träd för att representera hur algoritmen skulle välja dess drag. Varje delning i grenarna är ett annat drag AI eller motståndaren kan spela. Till vänster om raderna av noder skrev jag om spelaren maximerar eller minimerar går. Den nedre raden är alla styrelsestater med sina värden. Inuti var och en av dessa noder finns ett nummer och det är poängen vi tilldelar var och en av brädorna: ju högre de är, desto bättre är det för AI att ha.
Definitioner: överordnad nod - en nod som resulterar eller skapar noder under den; barnnodernas ursprung - noderna som kommer från samma föräldernod
De tomma noder representerar vilket drag AI kommer att göra för att komma till det bästa styrelsestillståndet. Det börjar med att jämföra barnen i noden längst till vänster: 10, -3, 5. Eftersom den maximaliserande spelaren skulle göra flytten, skulle den välja den dragning som skulle ge den flest poäng: 10. Så, vi väljer och lagrar det flytta med tavlan poäng och skriva det i föräldernoden. Nu när 10 är i föräldernoden är det nu minimeringsspelarnas tur. Noden som vi skulle jämföra 10 med är dock tom, så vi måste utvärdera den noden först innan den minimerande spelaren kan välja. Så vi går tillbaka till den maximerande spelarens tur och jämför barnen i den intilliggande noden: 8, -2. Maximering kommer att välja 8 och vi skriver det i den tomma föräldernoden. Nu när algoritmen har fyllt i de tomma utrymmena för barn i en nod ovanför den, kan den minimerande spelaren jämföra dessa barn - 10 och 8 och välja 8. Algoritmen upprepar sedan denna process tills hela trädet är fyllt. I slutet av det här exemplet har vi poängen 8. Det är det högsta brädläget AI kan spela för att anta att motståndaren spelar optimalt. Så AI kommer att välja det första drag som leder till 8 -tavlans tillstånd, och om motståndaren spelar optimalt bör AI spela alla drag för att komma till brädstatus 8. (Följ anteckningarna på mina bilder)
Jag vet att det var mycket. Om du är en av de typerna som behöver få någon att prata med dig för att förstå något, här är ett par videor som jag tittade på för att hjälpa mig att förstå tanken bakom detta: 1, 2, 3.
Steg 6: Minimax -algoritm: Pseudokod

När du har förstått logiken bakom minimax -algoritmen, ta en titt på denna pseudokod (de funktioner som är universella för alla koder) från wikipedia:
funktion minimax (nod, djup, maximizingPlayer) är
om djupet = 0 eller noden är en terminalnod då
returnera nodens heuristiska värde
om maximizingPlayer då
värde: = −∞
för varje nodebarn
värde: = max (värde, minimax (barn, djup - 1, FALSKT))
returvärde
annat (* minimera spelaren *)
värde: = +∞
för varje nodebarn
värde: = min (värde, minimax (barn, djup - 1, SANT))
returvärde
Detta är en rekursiv funktion, vilket innebär att den kallar sig om och om igen tills den når en stopppunkt. Först tar funktionen in tre värden, noden, djupet och vars tur det är. Nodvärdet är den plats där du vill att programmet ska börja söka. Djupet är hur långt du vill att programmet ska söka. Till exempel, i mitt trädexempel har det ett djup av 3, eftersom det sökte igenom alla tavlorna efter 3 drag. Naturligtvis skulle vi vilja att AI kontrollerar varje styrelse och väljer en vinnande vinst, men i de flesta spel där det finns tusentals om inte miljontals bordskonfigurationer kommer din bärbara dator hemma inte att kunna bearbeta alla dessa konfigurationer. Så vi begränsar AI: s sökdjup och får det att gå till den bästa styrelsen.
Denna pseudokod reproducerar processen som jag förklarade i de två föregående stegen. Låt oss nu ta detta ett steg längre och höger detta i pythonkod.
Steg 7: Gör din AI med Ai_template.py




Innan du tittar på min Minimax AI-kod, försök att skapa din egen AI med filen ai_template.py och pseudokoden som vi pratade om i det sista steget. Det finns två funktioner i ai -mallen som heter: def minimax_min_node (board, color) och def minimax_max_node (board, color). Istället för att minimax -funktionen kallar sig rekursivt, har vi två olika funktioner som kallar varandra. För att skapa den heuristiska för att utvärdera styrelsestater måste du skapa din egen funktion. Det finns färdiga funktioner i filen othello_shared.py som du kan använda för att bygga din AI.
När du har din AI, försök köra den mot, randy_ai.py. För att köra två ais mot varandra, skriv in "python othello_gui.py (infoga ai -filnamn).py (infoga filnamn).py" i mac -terminalen eller skriv "run othello_gui.py (infoga ai -filnamn).py (infoga filnamn).py "och se till att du är i rätt katalog. Titta också på min video för de exakta stegen.
Steg 8: Dags att få AI att slåss



Skaffa nu ett gäng av dina datorvänner och få dem att designa sin egen AI! Sedan kan du göra en tävling och få din AI -hertig att släppa ut den. Förhoppningsvis, även om du inte kunde bygga din egen AI, kunde du förstå hur minimax -algoritmen fungerar. Om du har några frågor är du välkommen att posta några frågor i kommentarerna nedan.
Rekommenderad:
Artificiell intelligens och bildigenkänning med HuskyLens: 6 steg (med bilder)

Artificiell intelligens och bildigenkänning med HuskyLens: Hej, vad händer, killar! Akarsh här från CETech. I det här projektet ska vi titta på HuskyLens från DFRobot. Det är en AI-driven kameramodul som kan utföra flera artificiell intelligensoperationer som Face Recognitio
Arduino "First Player" för brädspel: 4 steg
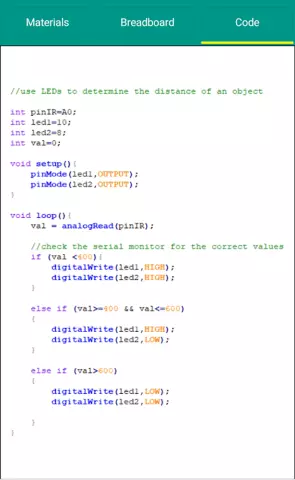
Arduino "First Player" för brädspel: Detta projekt inspirerades av " första spelaren " appar som jag och min man har använt på våra telefoner. Vi älskar att spela brädspel och använder " första spelare " appar för att avgöra vem som går först. Jag bestämde mig för att försöka göra min egen Arduino -version
Sätta ljud, ljus och rörelse i ett brädspel med magneter: 3 steg

Att sätta ljud, ljus och rörelse i ett brädspel med magneter: Detta projekt är ett försök att sätta elektronikkomponenter i ett brädspel. Magneter limmades på bonde och hallsensorer limmades under brädet. Varje gång en magnet träffar en sensor spelas ett ljud, en lysdiod tänds eller en servomotor utlöses. Jag ma
Artificiell intelligens för din robot: 7 steg
Artificiell intelligens för din robot .: Att få din robot att röra sig och få den att tänka är olika uppgifter. Hos människor styrs fina rörelser av lillhjärnan medan handlingar och beslutsfattande - av den stora hjärnan. Om du läser detta har du förmodligen redan en robot och kan hantera
Bygg din egen AI (artificiell intelligens) assistent 101: 10 steg

Bygg din egen AI (artificiell intelligens) -assistent 101: Kom ihåg tiden när du tittade på Iron Man och undrade för dig själv, hur coolt det skulle vara om du hade din egen J.A.R.V.I.S? Tja, det är dags att förverkliga den drömmen. Artificiell intelligens är nästa gen. Tänk vad häftigt det skulle bli
