
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:40.
- Senast ändrad 2025-01-23 15:10.

Principen för kurvspårning med AD2 beskrivs i följande länkar nedan:
https://www.instructables.com/id/Semiconductor-Cur…
https://reference.digilentinc.com/reference/instru…
Om den uppmätta strömmen är ganska hög är noggrannheten acceptabel. Men lägre strömmätning, brist på:
Förskjutningsfel och begränsning av vanligt läge för omfångskanalförstärkarna
Lutningsfel på grund av parallella motstånd
Dessa fel kan inte elimineras med AD2 -enhetskalibrering.
Steg 1: Kretsdiagrammet med AD2 interna lastmotstånd
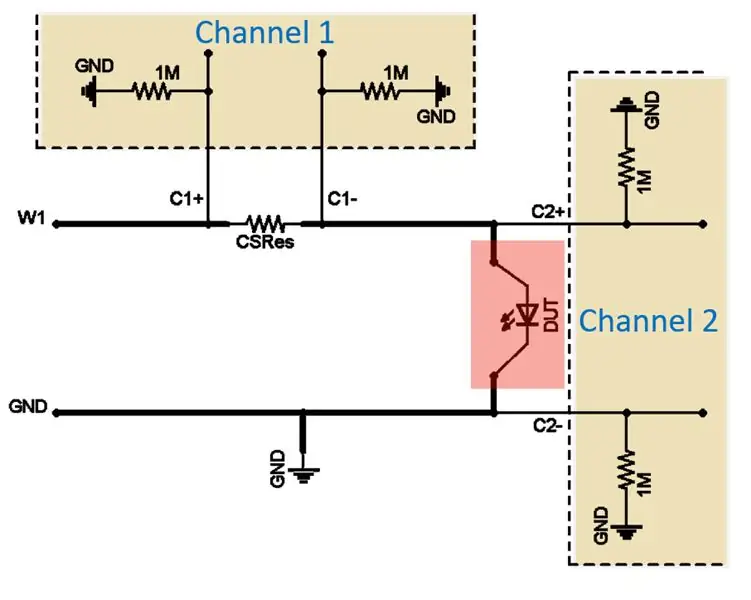
Det är anslutet vågformsgeneratorn (W1), omfångskanalen 1 känner av spänningsfallet på strömavkänningsmotståndet (CSRes) och kanalen 2 känner av spänningen på enheten som testas (DUT).
Steg 2: Ekvivalent kretsdiagram
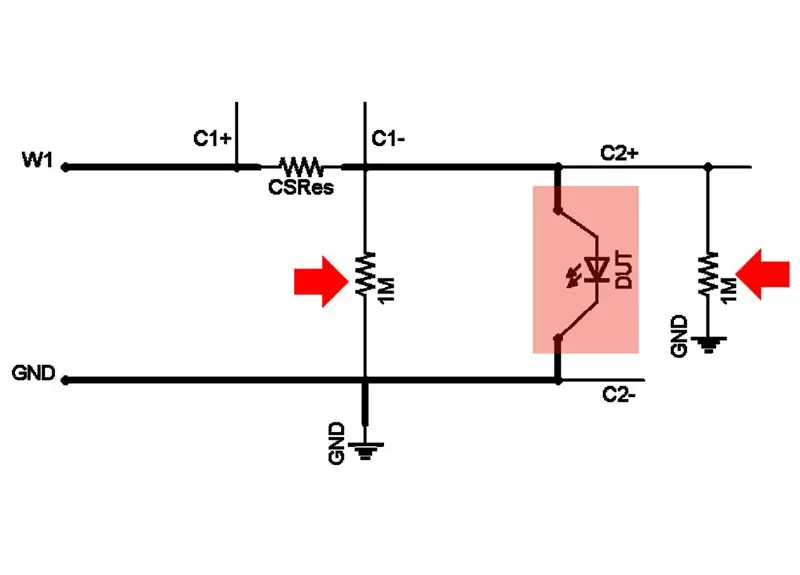
AD2-ingångsstiften har 1MOhm neddragningsmotstånd på varje ingångsstift som påverkar strömmätningen. Två av dessa motstånd är parallella med DUT.
Steg 3: Felets inverkan
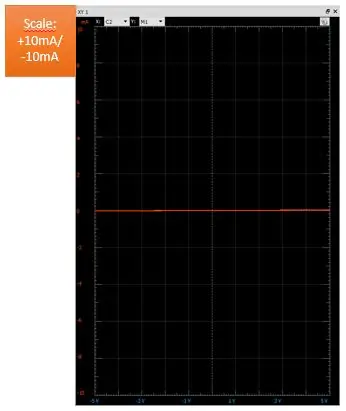
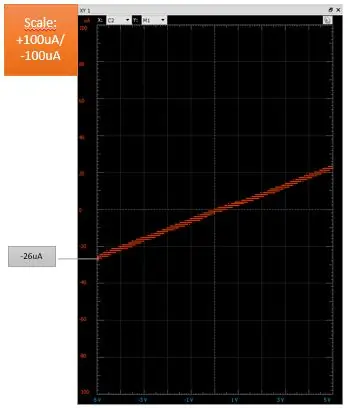
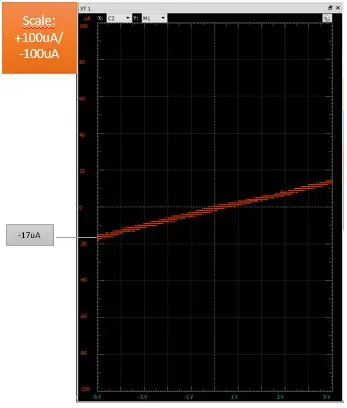
Vid ovanstående grafer kopplades DUT från. Nuvarande avkänningsmotstånd är 330Ohm
Vänster: Vertikal skala på +10mA/-10mA ser korrekt ut
- Överst till höger: Vertikal skala visar ett fel med ökad upplösning på +100uA/-100uA (parallellt motstånd på 500 kOhm till DUT och begränsad common mode-avvisning (CMRR) för omfångskanal 1 och förskjutningen är nästan noll)
- Nederst till höger: Vertikal skala är lika med bilden på toppen. Men här kortades det nuvarande avkänningsmotståndet. grafen visar endast CMRR-fel (5V/500kOhm = 10uA, 26uA-17uA = 9uA det är nära 10uA)
Steg 4: Felkompensation via linjär ekvation
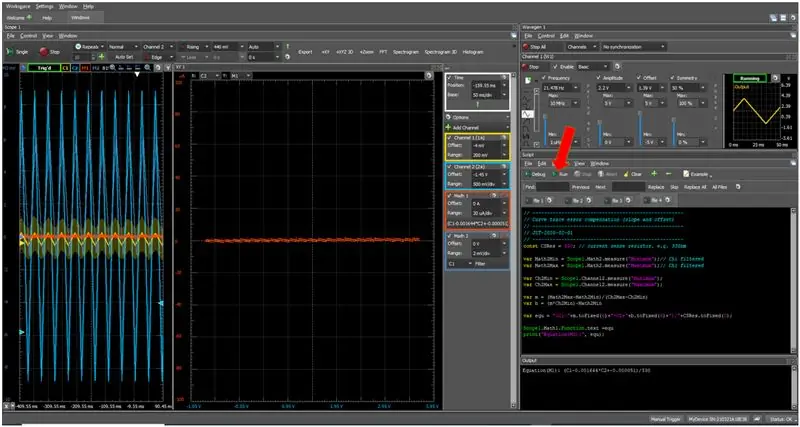
Ett kort skript kan göra detta automatiskt.
Hur fungerar det:
För att beräkna ekvationen krävs fyra parametrar:
Min/Max ch1 (ström) och även ch2 (spänning)
Eftersom spänningen vid ch1 är mycket låg är det därför Math2 -filtret ch1.
Slutligen kommer den beräknade ekvationen att skrivas till Math1.
Skriptet till höger körs genom att trycka på körknappen i skriptfönstret, utan ansluten DUT. Visas kommer Ch1 inte Math2, eftersom filtrering ger en viss fördröjning och som genererar dubbla linjer.
Steg 5: Skriptet
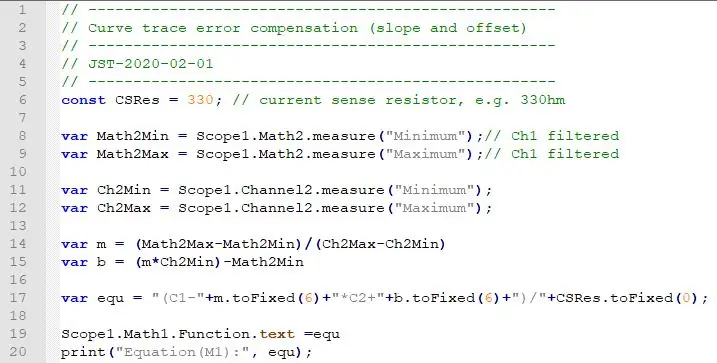
Detta är hela skriptet som eliminerar felen. En beskrivning av nyckelkommandona finns tillgänglig med hjälp av programmet Waveforms Application.
Steg 6: Matematiska inställningar
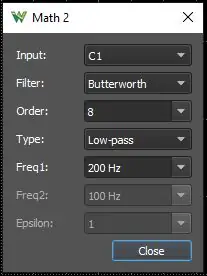
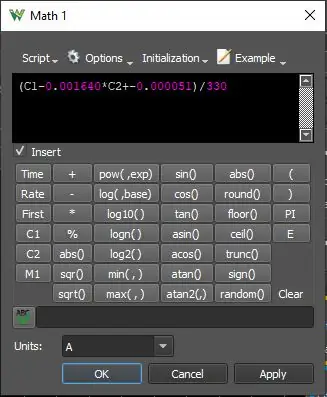
Math2 -filter Ch1, detta är nödvändigt för att beräkna Min/Max -parametern korrekt. Math1 visar den beräknade ekvationen.
Steg 7: DUT Exempel: LED
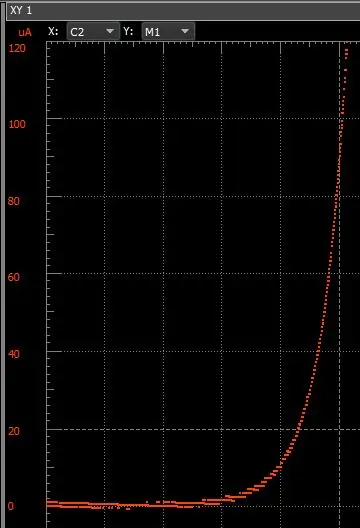
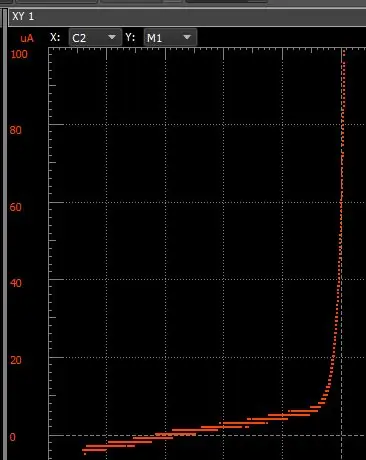
Den vänstra grafen visar beteendet med kompensation och det högra som vanligt. Det finns en signifikant skillnad synlig i högre strömupplösning.
Steg 8: Slutsats
Detta exempel visar AD2 -skriptspråkets kraftfulla förmåga. Lätt att använda, väldokumenterade AD2 -kommandon och utmärkt att felsöka.
Det finns AD2 -arbetsytafilen för nedladdning tillgänglig.
Varning ändra filtillägget till.zip och packa upp filen innan du använder den med AD2. Uppladdning av.zip -tillägget stöds inte av instruktioner.
Ett annat projekt finns tillgängligt på trenz electronic: LCR-Meter (Excel VBA)
Rekommenderad:
BBC Micro: bit and Scratch - Interactive Rat & Driving Game: 5 Steps (med bilder)

BBC Micro: bit and Scratch - Interactive Steering Wheel & Driving Game: Ett av mina klassuppgifter den här veckan är att använda BBC Micro: bit för att ansluta till ett Scratch -program som vi har skrivit. Jag trodde att detta var det perfekta tillfället att använda mitt ThreadBoard för att skapa ett inbäddat system! Min inspiration till scratch p
DIY Long Distance Best Friend Lights: 4 Steps (med bilder)

DIY Long Distance Best Friend Lights: Jag gjorde långdistanssynkroniserade lampor kända som " Best Friend " lampor. Det betyder bara att de hålls synkroniserade med den nuvarande färgen på den andra lampan. Så om du skulle byta en lampa grön, strax efter skulle den andra lampan bli grön
Tänd LED Holocron (Star Wars): Made in Fusion 360: 18 Steps (med bilder)

Tänd LED Holocron (Star Wars): Made in Fusion 360: Jag är mycket förtjusande när jag arbetar med Fusion 360 för att skapa något vackert, speciellt för att göra något med belysning. Varför inte göra ett projekt genom att kombinera Star Wars -film med belysning? Därför bestämde jag mig för att göra detta instruerbara projekt
Arduino MOOD-LAMP: 4 Steps (med bilder)

Arduino MOOD-LAMP: En stämningslampa är en lampa där du kan få en färg som du kan göra utan en person. Jag använder en stämningslampa för att skapa en programvara och använda en mikrokontroll av de eleganta och neopixlarna. Puedes regularle cualquier color por medio de p
Film in the Past: 7 Steps (med bilder)

Film in the Past: Mitt projekt är en kamera som styrs av en hallonpi som är fäst vid en hatt. Den här kameran är konstant på, den filmar allt, men spelar bara in de senaste 7 sekunderna med videor. Låt oss ta ett exempel, föreställ dig att du går på gatan och du ser
