
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:48.
- Senast ändrad 2025-01-23 15:11.
Denna instruerbara kommer att täcka några av de mest grundläggande funktionerna i matlab. Du kommer att lära dig hur man får matlab att köra en periodisk funktion internt och plotta och hur man kan dra samma periodiska funktion från en excel -fil istället och plotta den. Dessa funktioner är några av de mest grundläggande och används flitigt i matlab. Denna instruerbara är riktad till dig som aldrig har använt matlab förut och bara behöver utföra några enkla uppgifter med den. Koden som markeras i varje bild ingår som en kommentar så att du kan kopiera och klistra in koden. Ta gärna den här koden och ändra den för att passa din ansökan.
Steg 1: Starta Matlab
Det första steget är att få igång matlab så att vi kan börja arbeta med det. När du först startar matlab ska det se ut som skärmdumpen nedan. Det första steget är att tilldela en katalog för matlab att arbeta från. Det är här programmet kommer att hämta alla filer från och det är där du bör spara allt ditt matlab -arbete. Jag rekommenderar att du skapar en ny mapp någonstans du kommer ihåg den och namnger den något du kommer att känna igen. När du har skapat en ny mapp klickar du på "…" längst upp till höger på skärmen som markeras i den andra bilden. Detta kommer att dyka upp en bläddringsruta som visas på den tredje bilden. Hitta den nya mappen du skapade på din dator och välj den. I detta exempel heter filen "370" och finns på skrivbordet.
Steg 2: Skapa en M-fil
Det vi behöver göra är att skapa en ny M -fil. En M -fil fungerar precis som att skriva kod direkt i matlab, men du kan spara och ändra koden och köra den upprepade gånger. När du anger kod direkt i matlab skriver du varje kodrad individuellt. I en M -fil skriver du hela koden och kör den på en gång. För att öppna en ny M -fil klickar du på filen. Placera markören på "Ny" och klicka sedan på "Tom M -fil" som visas på den första bilden. Det som öppnas ska se ut som den andra bilden. Eftersom denna kod kan köras upprepade gånger är det en bra idé att stänga allt och rensa alla variabler innan det körs varje gång. Detta uppnås genom två rader kod: close allclear allSom det ses på den tredje bilden ser du till att allt rensas och stängs.
Steg 3: Skapa en tidsvektor
Det första vi ska göra är att skapa ett diagram över en funktion i matlab. Det första steget är att skapa den oberoende variabeln. I det här fallet kommer vi att kalla det "t" för tiden. Metoden vi kommer att använda för att skapa denna variabel är att skapa en vektor. En vektor är i grunden en serie tal. Till exempel skulle 1, 2, 3, 4 vara en kort vektor. Koden för att skapa denna vektor är: t = 0,1: 0,01: 10; Det första talet, 0,1 refererar till startpunkten. Det andra talet, 0,01 refererar till stegstorleken. Det tredje talet, 10, hänvisar till slutpunkten. Så denna vektor motsvarar 0,1, 0,11, 0,12 … ända upp till 10. För att se om vektorn skapades, klicka på den gröna körknappen som markeras i den andra bilden. Detta kör programmet. För att se vår vektor, gå till huvudfönstret för matlab. Klicka på skrivbordet, sedan muspekaren över skrivbordslayout och klicka sedan på standard som beskrivs i den tredje bilden. Nu ska din skärm se ut som den fjärde bilden. Till höger ser du vår nyskapade variabel, t. Dubbelklicka på den och som på den femte bilden ser du serien med siffror som skapats.
Steg 4: Köra och rita en funktion
Nu ska vi rita en funktion skapad i matlab. Det första steget är att skapa funktionen. Detta är så enkelt som att skriva ut den önskade matematiska funktionen. Ett exempel visas på den första bilden. Koden som används för denna funktion är: y = sin (t)+4*cos (5.*t).^2; Perioden före multiplikationen i cosinus, och innan cosinusens kvadrat säger till matlab att utföra dessa funktioner helt enkelt på tidsvektorns värdesaker, inte att behandla tidsvektorn som en matris och försöka göra matrisfunktioner på den. Nästa steg är att skapa själva figuren. Detta uppnås med hjälp av koden som visas i den andra figuren. Ordningen på variablerna i plotkommandot är mycket viktig, så se till att ställa in din kod precis som den är konfigurerad nedan. Figurh = axes ('fontsize', 14); plot (t, y, 'linewidth, 2) xlabel ('Tid (ar)') ylabel ('Y -värde') Titel ('Y -värde vs tid') rutnät Slutligen klickar du bara på den gröna körpilen igen och siffran ska dyka upp som på den tredje bilden.
Steg 5: Dra data från Excel
Vi kommer nu att skapa samma graf som tidigare, men genom att importera funktionsdata från ett Excel -kalkylblad. Den första bilden är en skärmdump av Excel -kalkylbladet som kommer att användas. Det är exakt samma datapunkter som skapades i matlab i de föregående stegen, bara gjorda i excel. För att börja kan vi ta bort koden som skapar vår tidsvektor och koden för vår funktion från de föregående stegen. Din kod ska nu se ut som den andra bilden. Sätt in koden som visas i den övre röda rutan på den tredje bilden. Detta är koden för att läsa excel -filen. "A" hänvisar till en matris som innehåller alla siffror i kalkylarket, och "B" inkluderar all text från kalkylarket. Variablerna t och y dras från den första och andra kolumnen som visas i koden. [A, B] = xlsread ('excelexample.xlsx'); t = A (:, 1); y = A (:, 2); Sifferkoden kan också ändras enligt den nedre röda rutan på den tredje bilden. Detta kommer faktiskt att dra diagramtiteln och axeletiketterna från kalkylarket och lägga dem på din graf. Xlabel (B (2)) ylabel (B (3)) Titel (B (1)) Det sista du ska göra är att köra programmet igen och du kommer att se samma figur dyka upp som på den sista bilden.
Steg 6: Skapa ett specgram
I det här steget kommer vi att använda matlab för att skapa ett specgram genom att läsa en wav -ljudfil. Ett specgram kallas ibland för en "2,5D -graf", eftersom den använder en tvådimensionell graf, med tillägg av färg för att visa amplitud. Färgen ger mer detaljer än ett enkelt 2D -diagram, men inte detaljerna i ett 3D -diagram, därav termen "2.5D." Matlabs specgram -funktion tar en uppsättning datapunkter från wav -filen och utför en Fourier -transformering på punkter för att bestämma frekvenserna i signalen. För detta instruerbara är det inte viktigt att veta hur en Fourier -transform fungerar, bara veta att specgrammet kommer att plotta vilka frekvenser som finns och hur starka de är med avseende på tid. Funktionen plottar tid på X-axeln och frekvens på Y-axeln. Styrkan för varje frekvens visas med färg. I detta fall är wav -filen en ljudinspelning av en metallbit som träffas, och sedan spelas metallens vibrationer som ljud. Med hjälp av specgrammet kan vi enkelt bestämma resonansfrekvensen för metallbiten, eftersom det är den frekvens som kvarstår längst med tiden. För att utföra denna uppgift måste du först matlab läsa wav -filen med hjälp av följande kod: [x, fs] = wavread ('flex4.wav'); I det här fallet är flex4.wav titeln på vår wav -fil, variabeln x är datapunkterna i filen och fs refererar till samplingsfrekvensen. För att utföra specgrammet, skriv bara följande kod: specgram [x (:. 1), 256, fs]; 256 motsvarar frekvensen som FFT utförs vid analys av data. Matlab hackar i princip ljudfilen i bitar och tar en FFT på varje bit. 256 berättar hur stor varje bit ska vara. Detaljerna för detta är inte viktiga, och 256 är ett säkert värde att använda för de flesta applikationer. Om du nu kör koden kommer du att se en figur som dyker upp på den andra bilden. Av detta är det lätt att se att resonansfrekvensen motsvarar den röda toppen i det nedre högra hörnet av figuren. Detta är toppen som kvarstår längst med tiden.
Rekommenderad:
VBScript Basics - Starta dina skript, fördröjningar och mer !: 5 steg

VBScript Basics - Starta dina skript, fördröjningar och mer !: Välkommen till min första handledning om hur man gör VBScripts med anteckningsblock. Med.vbs -filer kan du skapa några roliga upptåg eller dödliga virus. I den här självstudien kommer jag att visa dig grundläggande kommandon som att starta ditt manus, öppna filer och mycket mer. Vid t
Reckless Racer Arduino OLED Game, AdafruitGFX och Bitmaps Basics: 6 steg

Reckless Racer Arduino OLED Game, AdafruitGFX and Bitmaps Basics: I denna handledning kommer vi att titta på hur man använder bitmappar med Adafruit_GFX.c -biblioteket som en slags sprites i ett spel. Det enklaste spelet vi kan tänka oss är ett bilrullebyte med sidorullande körfält, i slutändan vår betatestare och assistentkodare för
Gränssnittsknapp - Arduino Basics: 3 steg
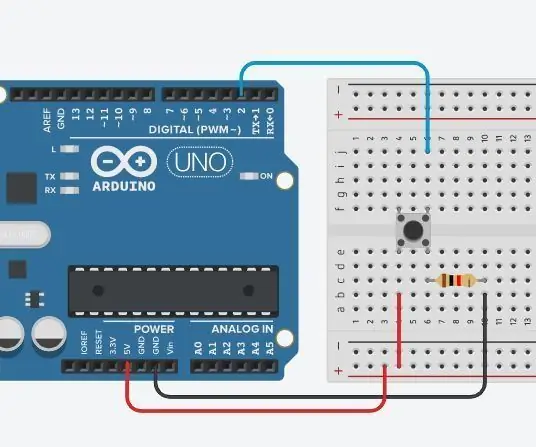
Gränssnittsknapp - Arduino Basics: Tryckknappen är en komponent som ansluter två punkter i en krets när du trycker på den. När tryckknappen är öppen (utan tryck) finns det ingen anslutning mellan tryckknappens två ben, så stiftet är anslutet till 5 volt (genom pull-up resi
Animatronics Basics - Servomotorn: 8 steg

Animatronics Basics - Servomotorn: Oavsett om det är en jolig semestervisning i fönstret på ett varuhus eller en skrämmande Halloween -upptåg, lockar ingenting uppmärksamhet som en animerad marionett. Dessa elektroniskt styrda animationer kallas ibland " animatronics " och det
IoT Basics: Ansluta din IoT till molnet med Mongoose OS: 5 steg

IoT Basics: Ansluta din IoT till molnet med hjälp av Mongoose OS: Om du är en person som håller på med pyssel och elektronik, kommer du oftare än inte att stöta på begreppet Internet of Things, vanligtvis förkortat som IoT, och att det refererar till en uppsättning enheter som kan ansluta till internet! Att vara en sådan person
