EWEEDINATOR☠ Del 4: Differential Steering Geometry Code: 3 Steps

2025 Författare: John Day | [email protected]. Senast ändrad: 2025-01-23 15:11

Om du har tid att titta på videon ovan kommer du att märka att det är några konstiga ljud som orsakas av att motorerna på ratten stannar då och då när WEEDINATOR navigerar en 3 -punkts sväng. Motorerna fastnar i huvudsak mot varandra eftersom svängradien är annorlunda på insidan och utsidan och avståndet som hjulet färdas är olika per varvningsgrad.

Vridningens geometri kan beräknas genom att skissa ut ungefär 8 permutationer av svängen, vilket ger exempel på vridning i olika vinklar på det inre hjulet från 0 (ingen varv) till 90 (full lås) grader. Låter komplicerat?

De flesta robotar med små hjul försöker inte ha någon form av sofistikerad styrning och förlitar sig mycket effektivt på att helt enkelt ändra motorernas relativa hastighet på varje sida av fordonet, vilket är ungefär detsamma som hur en bandgrävare eller tank Arbetar. Det här är bra om du laddar över en kraterfylld krigszon som skjuter på allt som rör sig, men i en lugn jordbruksmiljö är det viktigt att göra så lite skada på marken och marken som möjligt så att slipa hjul fram och tillbaka mot varandra är inte lämpligt!

De flesta bilar och traktorer har en mycket användbar pryl som kallas en "Differential", förutom bilarna du ser i gamla amerikanska filmer där du kan höra däcken som skrattar varje gång de går runt ett hörn. Bygger amerikaner fortfarande bilar så här? Med WEEDINATOR kan vi programmera differential i drivmotorerna genom att räkna ut formeln för de relativa varvtalen och vinklarna på hjulen vid en viss svängvinkel. Låter det fortfarande komplicerat?

Här är ett snabbt exempel:

Om WEEDINATOR navigerar en sväng och har sitt inre hjul i 45 grader, är det yttre hjulet INTE 45 grader, det är mer som 30 grader. Dessutom kan det inre hjulet svänga i 1 km/timme, men det yttre hjulet kommer att vara betydligt snabbare, mer som 1,35 km/timme.

Steg 1: Geometriinställning

Några grundläggande antaganden görs till att börja med:

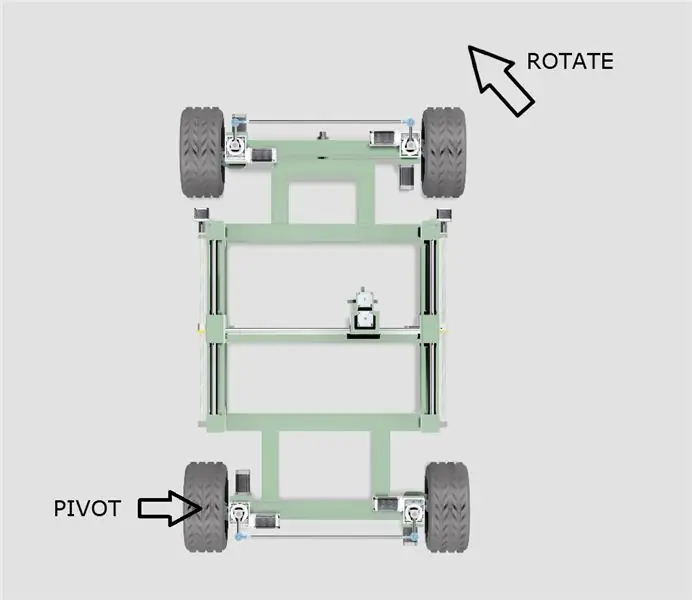
• Chassit kommer att svänga runt ett av bakhjulen enligt diagrammet ovan.
• Den effektiva mitten av svängcirkeln kommer att röra sig längs en linje som sträcker sig från mitten av de två bakhjulen, beroende på svängvinkeln.
• Geometrin kommer att ha formen av en sinuskurva.

Steg 2: Skalade ritningar av hjulvinklar och radier

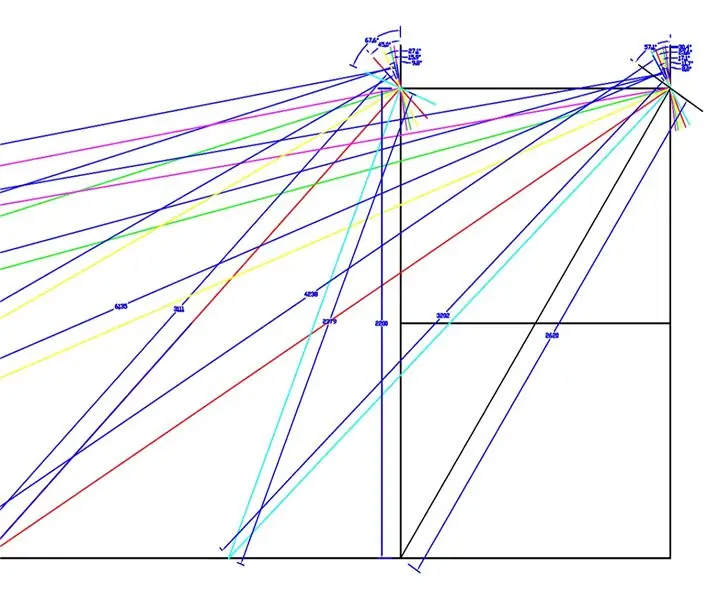
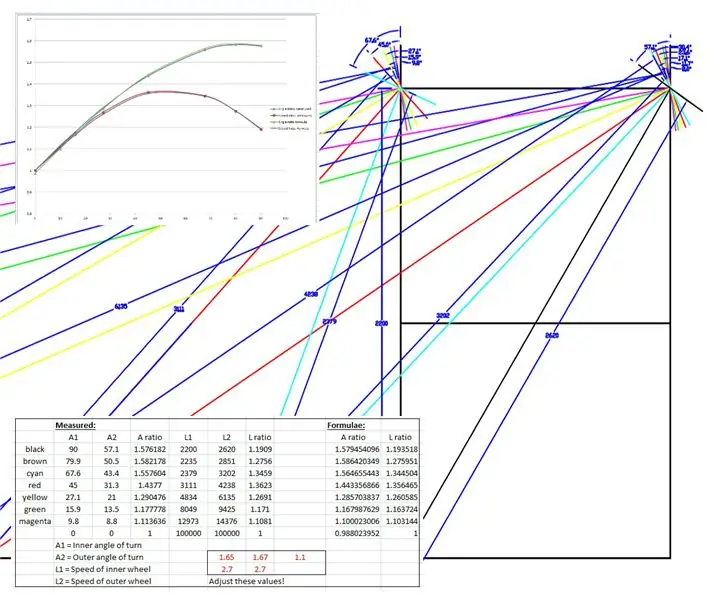
En ritning i full skala gjordes av WEEDINATOR -framhjulen och chassit med 8 olika permutationer av inre hjulvinkel mellan 0 och 90 grader och respektive svängcentra kartlades som visas på ritningarna ovan.

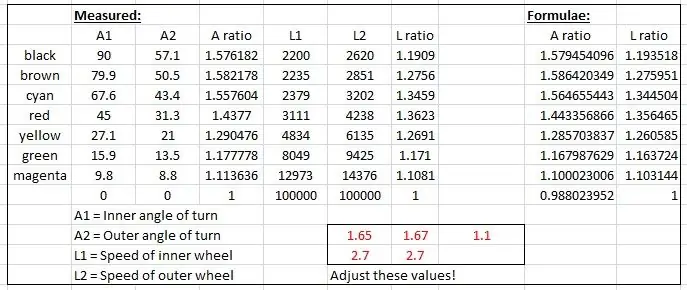
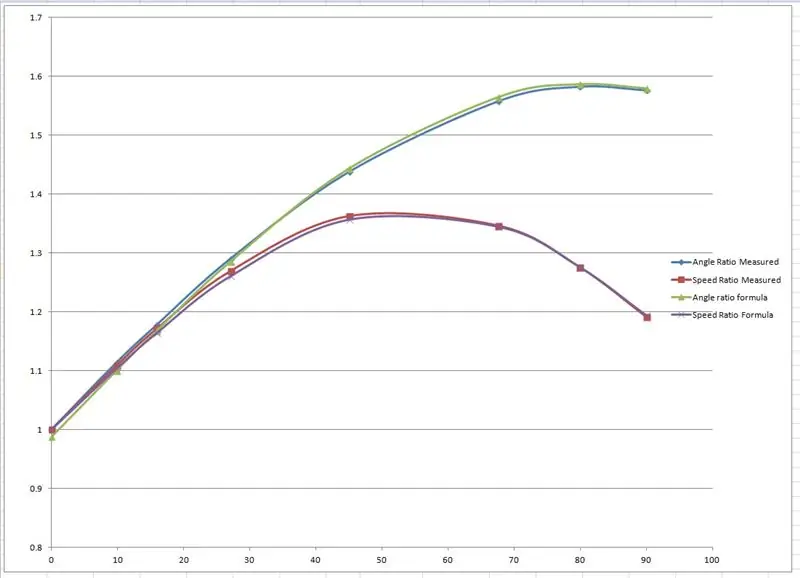
De effektiva radierna mättes från ritningen och ritades på ett diagram i Microsoft Excel.

Två grafer togs fram, en av förhållandet mellan vänster och höger framhjulsaxel och en annan för förhållandet mellan de två radierna för varje viss svängvinkel.

Jag "fudged" upp några formler för att efterlikna de empiriska resultaten baserat på en sinuskurva. En av fudgen ser ut så här:

speedRatio = (sin (inre*1,65*pi/180) +2,7)/2,7; // inre är den inre svängvinkeln.

Kurvorna fuskades genom att ändra värdena som visas i rött i excelfilen tills kurvorna passade ihop.

Steg 3: Kodning av formlerna

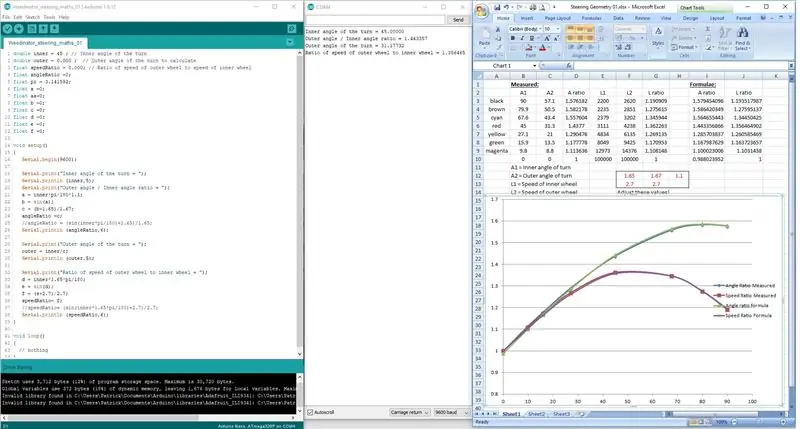
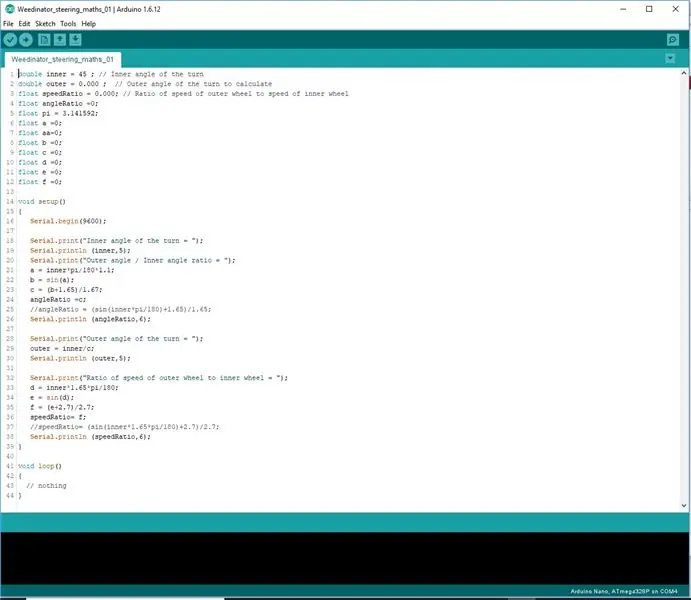
I stället för att försöka koda formlerna på en rad, delades de upp i tre steg för att tillåta Arduino att bearbeta matematiken korrekt.

Resultaten visas i seriell portdisplay och kontrolleras med de uppmätta resultaten på skalritningen.