Hur man skapar en Geodesic Dome i Temcor-stil i Autodesk Inventor: 8 steg

2025 Författare: John Day | [email protected]. Senast ändrad: 2025-01-23 15:11

Denna handledning visar dig hur du skapar en kupol i Temcor-stil med bara lite matematik.

Merparten av informationen i denna handledning hämtades från TaffGochs omvända konstruktion av indelningsmetoden för den gamla Amundsen-Scott South Pole Station, så ett stort tack till honom!

En stor fördel med Temcor -kupoler är deras låga unika strutantal - det ökar aritmetiskt med frekvensen, inte till skillnad från Duncan Stuarts vanliga triakontahedral geodesiska rutnät (metod 3*), men resultatet ser mycket mer tilltalande ut.

För enkelhetens skull är frekvensen för kupolen vi gör 14, så ackordfaktorerna kan krysskontrolleras mot TaffGochs Temcor-modell.

Inventor 2016.ipt ingår i slutet av självstudien.

*UPPDATERING*

Jag beskrev metod 4 som Duncan Stuarts vanliga triakontahedral geodesiska rutnät, men det är det inte. Metoden uppfanns faktiskt av Christopher Kitrick, som i sin artikel från 1985, "Geodesic Domes", beskrev dess konstruktion. I sin artikel från 1990, "A Unified Approach to Class I, II & III Geodesic Domes", beskriver han dessutom 8 andra metoder, en av dem är Duncan Stuarts metod 3, den andra hans egen "metod 4", och överraskande nog, en metod som liknar Temcors, som han kallar "Metod aa" (Steg 7 visar hur Temcor modifierade "Metod aa"). I en framtida instruerbar, kommer jag att beskriva konstruktionen av metoderna som beskrivs i den senare uppsatsen.

Steg 1: Användarparametrar

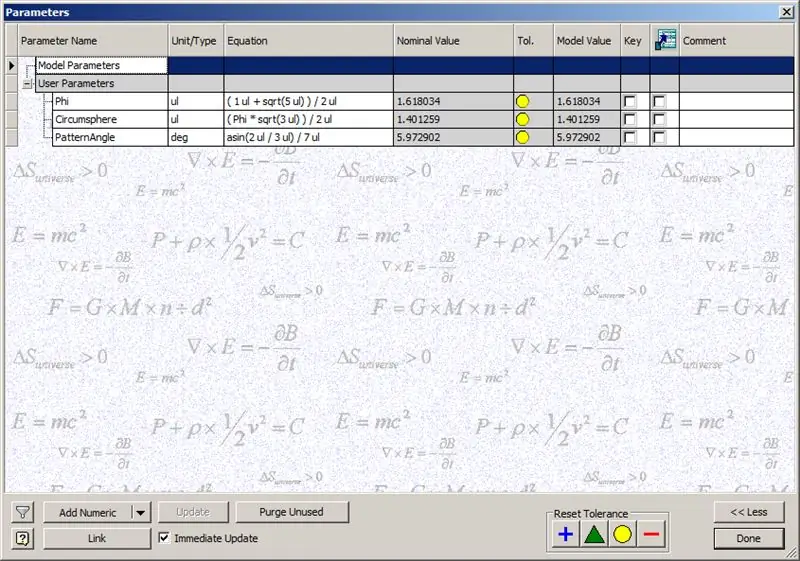
Innan vi börjar bygga kupolen anger du parametrarna som visas:

Phi - The Golden Ratio. Definieras som ((1+√5/) 2

Circumsphere - Detta är cirkumsfären hos en dodekaedron, definierad som ((Phi*√3)/2)

PatternAngle - Detta är den centrala vinkeln för en dodekaeder. Eftersom frekvensen för vår kupol är 14 delar vi denna centrala vinkel med halva frekvensen, i detta fall 7.

Steg 2: Skissa en gyllene rektangel

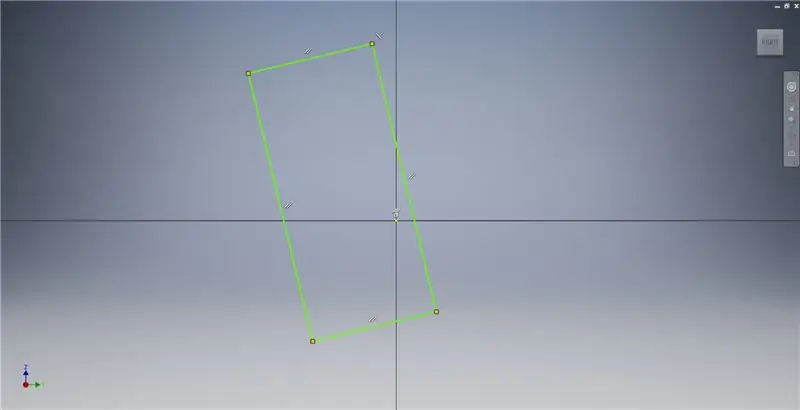
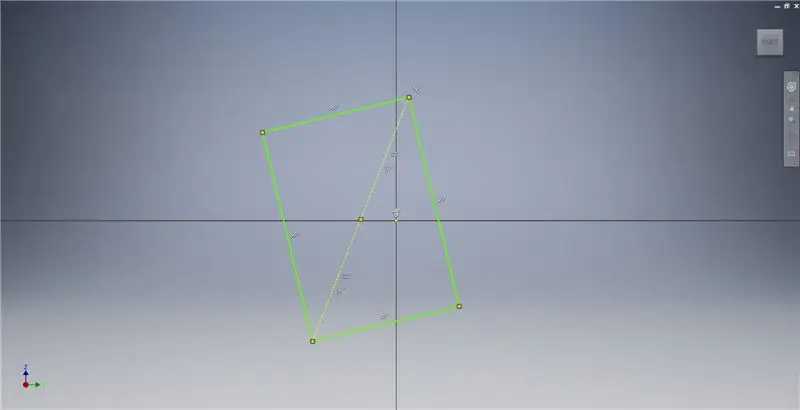
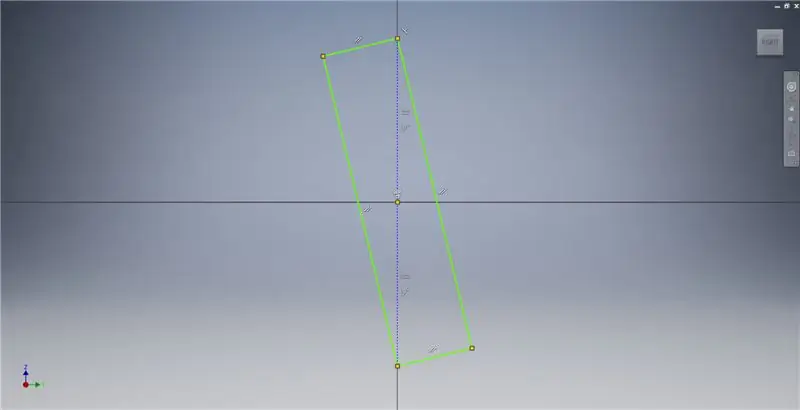
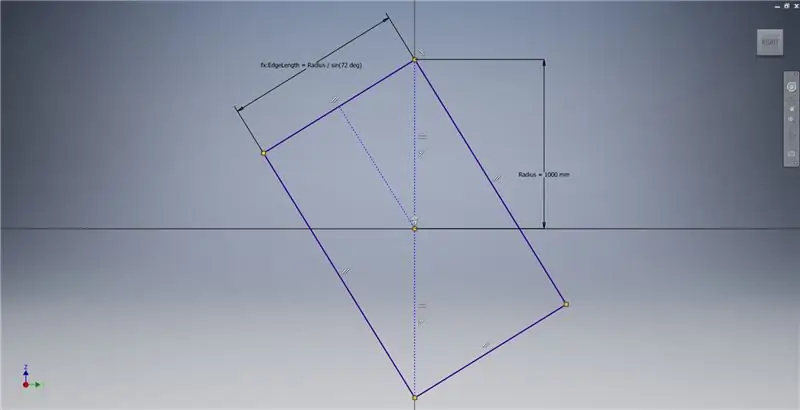
Starta en skiss på YZ -planet och skapa sedan en trepunkts rektangel som visas, med hänvisning till bildanteckningarna för ytterligare information som beskriver skapandet av en gyllene rektangel.

Steg 3: Skapa en Golden² -rektangel

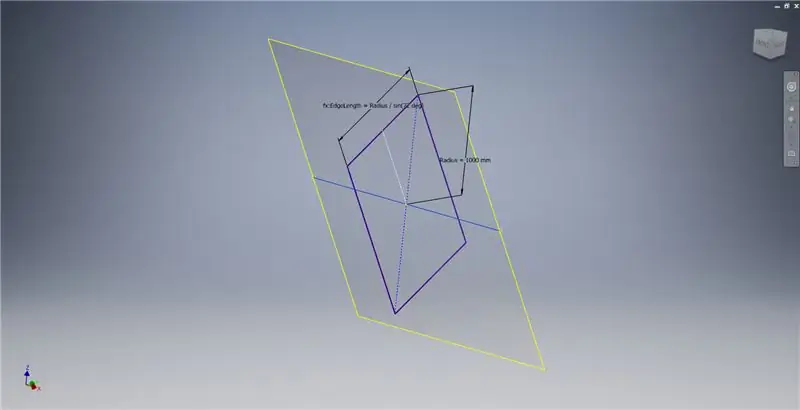
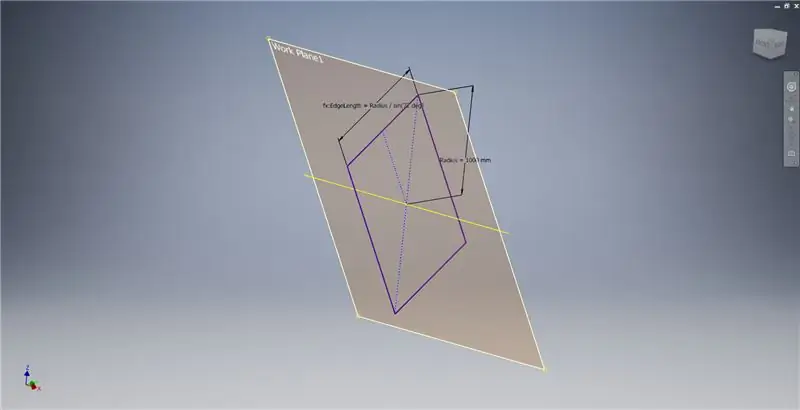
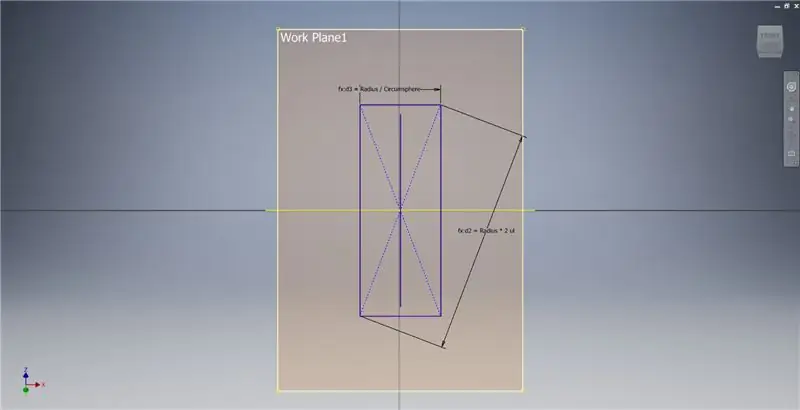
Skapa ett arbetsplan med hjälp av X -axeln och linjen markerad i den första bilden och starta sedan ytterligare en skiss på detta arbetsplan. Konstruera en mittpunkts rektangel med utgångspunkt från ursprunget, dimensionera sedan rektangeln som visas i den tredje bilden.

Steg 4: Skapa 2v Triacon Triangle

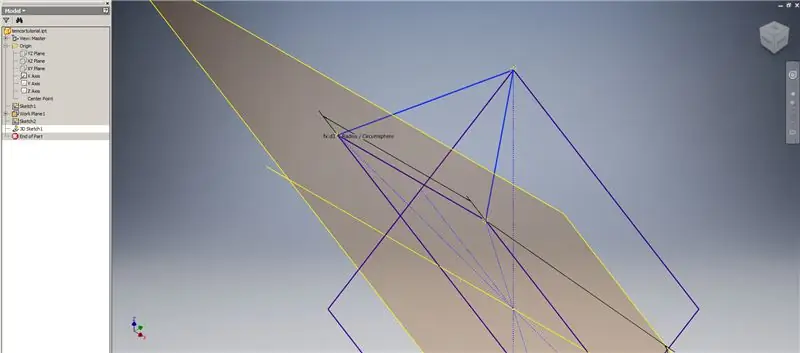
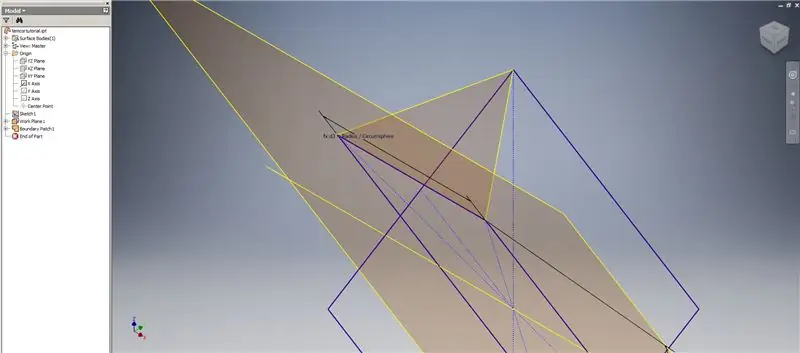
Nu när vi har all geometri vi behöver, bilda gränspatchen i den andra bilden med vilken metod du än föredrar. Jag valde att göra en 3D -skiss, men att skissa på ett annat arbetsplan skulle fungera lika bra.

Steg 5: Skapa korsningsplanen

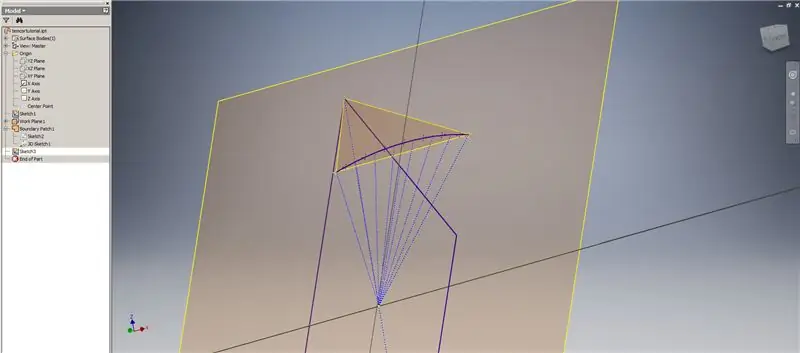
Starta ytterligare en skiss på det första arbetsplanet ("Work Plane 1") som du skapade, projicera hörnen på Golden² -rektangeln, anslut sedan dessa punkter och ursprunget för att bilda den centrala vinkeln på 2v triacontahedron. Dela den med halva kupolens frekvens, som om du startade en metod 2 -uppdelning. Placera punkter på mitten av ackorden.

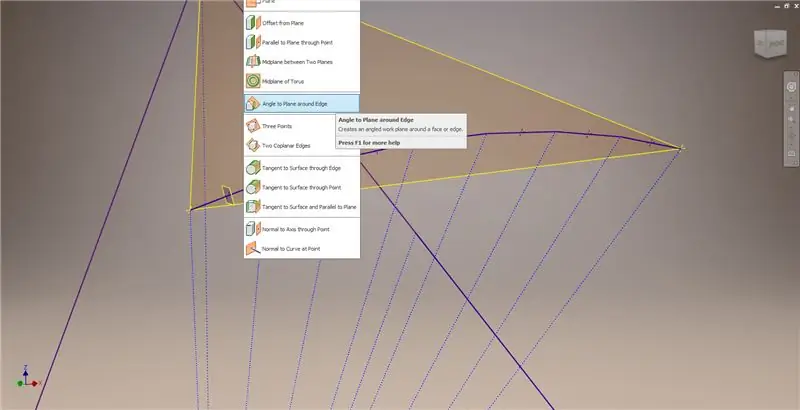
Avsluta skissen, skapa sedan ett plan med ett av ackorden och dess mittpunkt, som visas i den andra bilden. Skapa sedan ett annat arbetsplan med "Vinkel mot plan runt kanten". Välj arbetsplan 1 och en av konstruktionslinjerna som visas i mitten till höger och nedre vänstra bilden. Acceptera standardvinkeln på 90 grader, annars skulle resten av underavdelningen inte se rätt ut. Upprepa processen med resten av ackorden och konstruktionslinjerna för att få resultatet i den nedre högra bilden.

Steg 6: Skapa skärningskurvorna och bilda underavdelningen

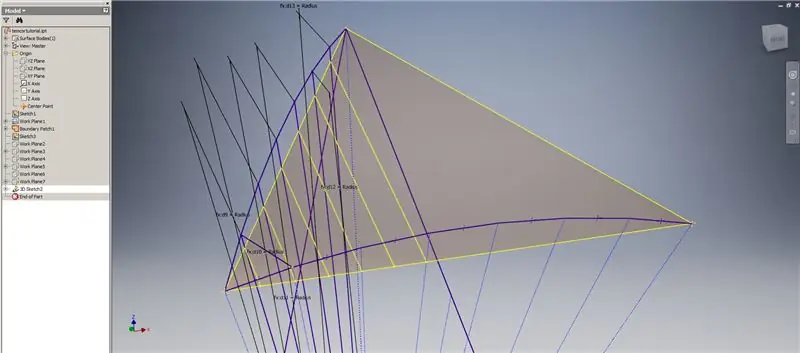
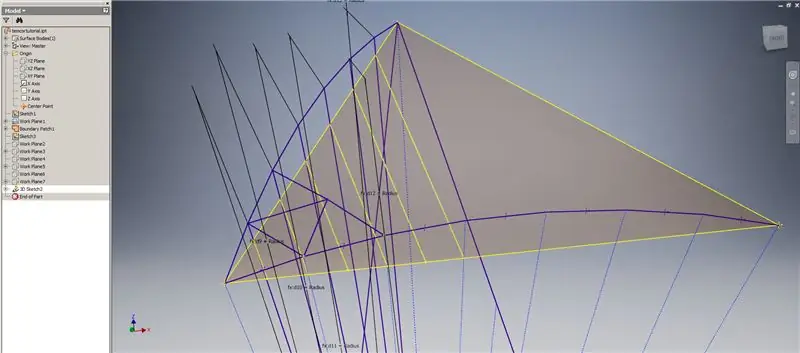
Starta en 3D -skiss och skapa sedan skärningskurvor med hjälp av arbetsplanen du just skapade och gränspatchen och bilda linjerna som visas i den översta bilden.

Rita linjer som sammanfaller med ändpunkterna för skärningskurvorna som visas i bild 2. Gör dem alla lika med kupolens radie. Rita ackorden som förenar linjerna som ligger på skärningskurvorna. Anslut någon geometri som ser tillräckligt nära ut för att bilda en triangel i underavdelningen. Se de följande tio bilderna för vilka ackord ska speglas över skärningsplanen - de kan förklara det bättre än bara ord.

Steg 7: Slutföra kupolen

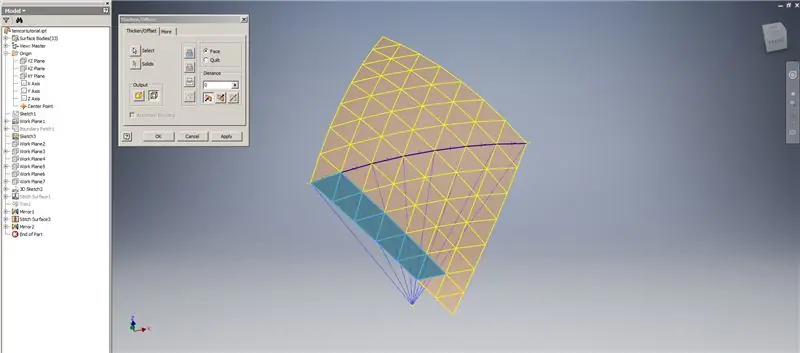
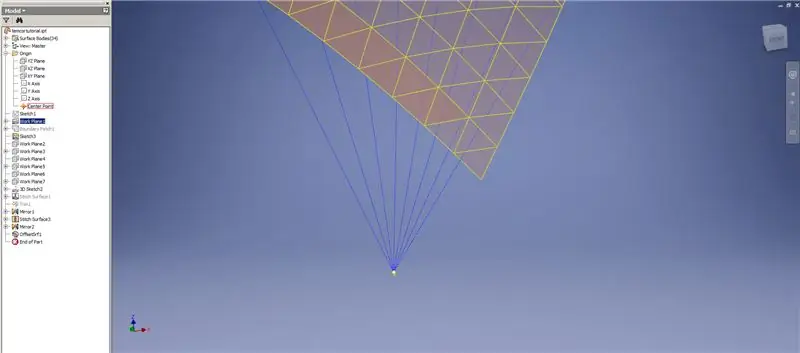
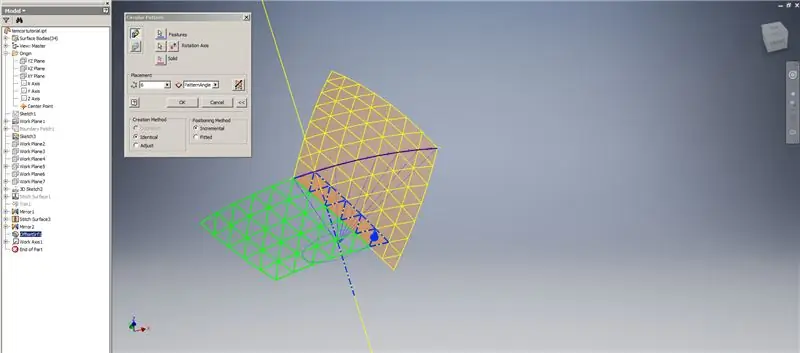
Skapa en tjockare/förskjutning av de nedre raderna, utelämna de två sista raderna med trianglar. Mönster den nya OffsetSrf 6 gånger, eller ((Frequency = 14)/2) -1. Dölj OffsetSrf, sy de mönstrade ytorna och spegla sedan den syade ytan med YZ -planet. Skapa arbetsplan som vilar på hörnen i den övre triangeln, som visas i bild 6. Trimma de sömda och speglade ytorna med hjälp av dessa nya arbetsplan, sy sedan ihop de återstående ytorna. Mönstra denna sista yta över Z -axeln, sy sedan ihop dessa sista ytor och du är klar!

Steg 8: Kontroll av ackord

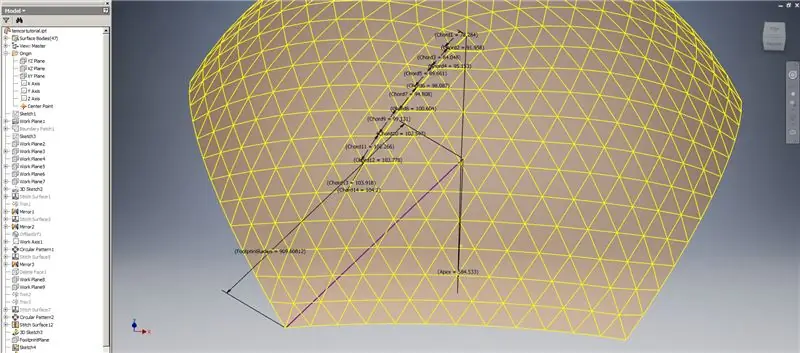
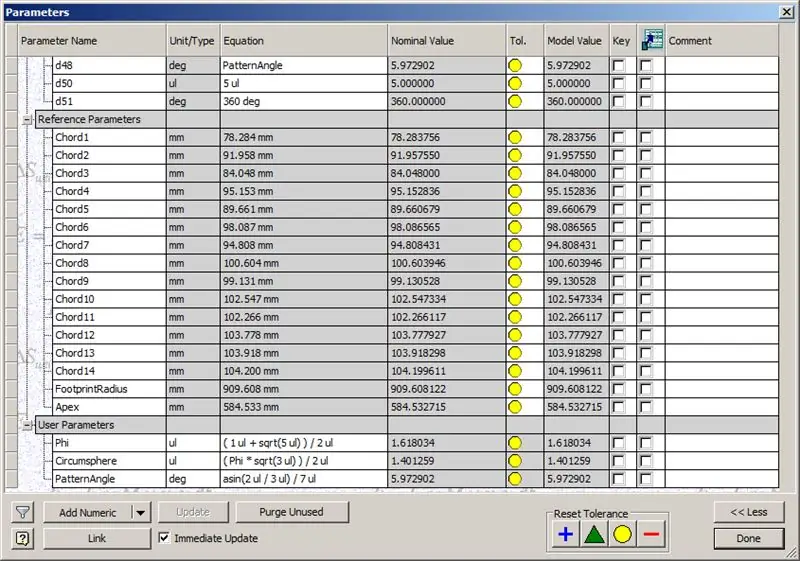
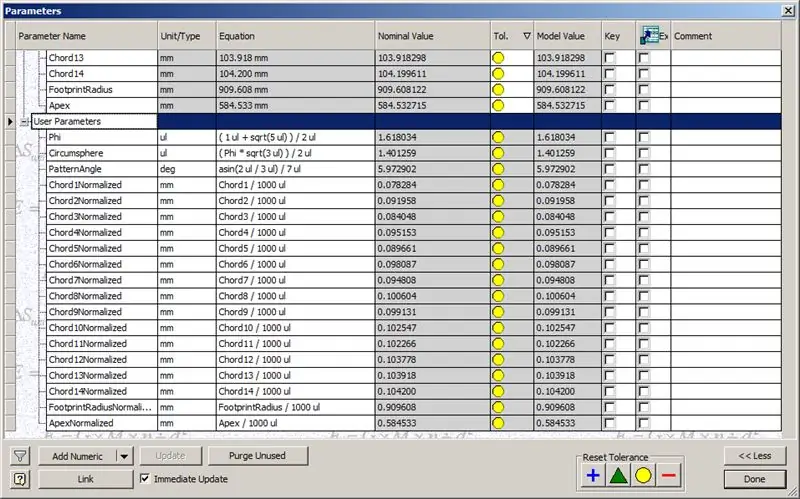
Så vår kupol är klar, men låt oss se om siffrorna matchar TaffGochs modell:

Med referensparametrarna ser det ut som att de passar perfekt!

Genom att dela ackordlängderna med 1000 kan vi tydligt se en perfekt överensstämmelse med ackordfaktorerna i TaffGochs modell, samt fotavtrycksradie och spetsfaktorer.