Vet du om ESP32 ADC -justering ?: 29 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:45

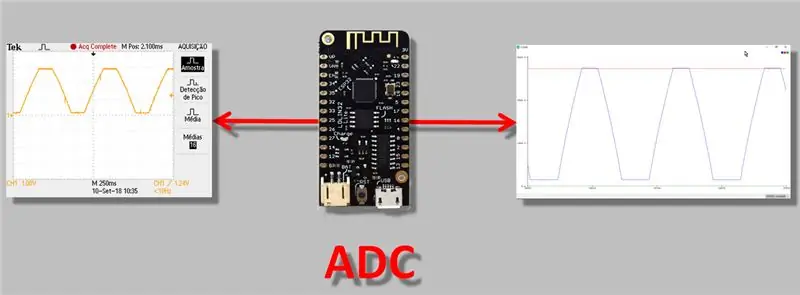
Idag ska jag prata om en mer teknisk fråga, men en som jag tror att alla som arbetar med ESP32 borde veta: frågan om ADC (analog-till-digital-omvandlare) läsjustering. Jag tycker att detta är viktigt eftersom när du gör en "mätning", särskilt med ett instrument som har en analog utgång, måste du vara helt säker på att avläsningen utförs korrekt.

I videon i dag kommer vi därför att utföra mätningar med hjälp av "analog-digital-omvandlaren" i ESP32, observera konverteringsavvikelserna och tillämpa en ADC-justerings- / kalibreringsmetod.

Steg 1: Vad är en AD -omvandlare?

En AD -omvandlare är en krets som kan översätta en analog (kontinuerlig) kvantitet till digitala (diskreta) värden. Vad betyder det? Det betyder att medan digitala värden bara kan anta diskreta värden som bildas av kombinationen av nollor och enor, kan en analog kvantitet anta vilket värde som helst inom ett intervall. Till exempel, om vi mätte spänningen i en ideal AA -cell, kan vi hitta valfritt värde mellan 0V och 1,5V, eftersom detta är analog kvantitet. Utgångstillståndet för en ideallampa måste endast anta två tillstånd (av eller på), vilket är en diskret storlek. Eftersom mikrokontroller fungerar med denna diskreta logik behöver vi en krets som kan översätta en analog mängd till digital (eller diskret).

Steg 2: Resurser som används

• Ett Lolin32 Lite -kort v1.0.0

• Ett Tektronix TDS1001C -oscilloskop för inspelning

• En USB -kabel för ESP32

• Ett Hantek DSO4102C -oscilloskop som signalgenerator

Steg 3: ESP32 ADC

Enligt Espressif-data kan ESP32-chipsen uppvisa en +/- 6% skillnad från ett chip till ett annat i de uppmätta resultaten.

Dessutom har konverteringen INTE ett linjärt svar för varje tillgängligt intervall för läsning. Espressif tillhandahåller en metod för kalibrering och föreslår att användare implementerar andra metoder om de anser det nödvändigt för att uppnå önskad noggrannhet.

Vi kommer att utföra ett datainsamling, och från detta kommer vi att visa ADC -svaren och ett exempel på att tillämpa en matematisk process för att läsa justeringen.

Det finns flera (enklare eller mer komplexa) sätt att utföra dessa korrigeringar. Det är upp till dig att utvärdera det mest lämpliga för ditt projekt.

Den som visas här kommer att ha ett illustrativt syfte och försöka ta itu med intressanta punkter som kan observeras under justeringar.

Steg 4: Krets används

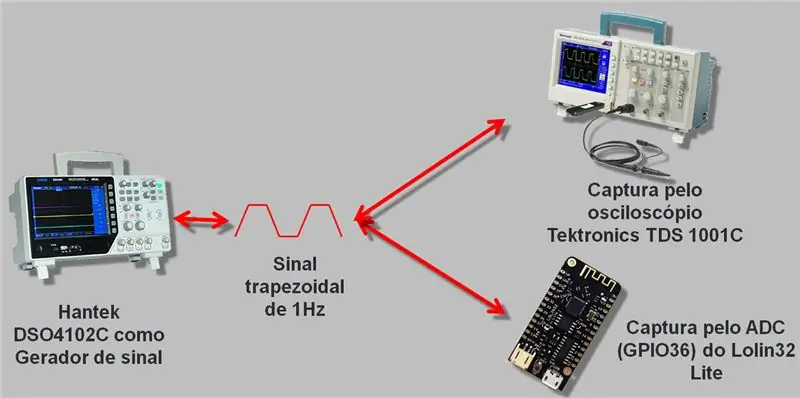
Jag använde ett oscilloskop med en signalgenerator som går upp till 25 MHz, Hantek DSO4102C. Vi genererade en våg som lästes av ESP A / D och oscilloskopet. Uppgifterna som samlats in spelades in i csv och i ett kalkylblad, som jag lämnar i slutet av artikeln för nedladdning.

Steg 5: Skylt används

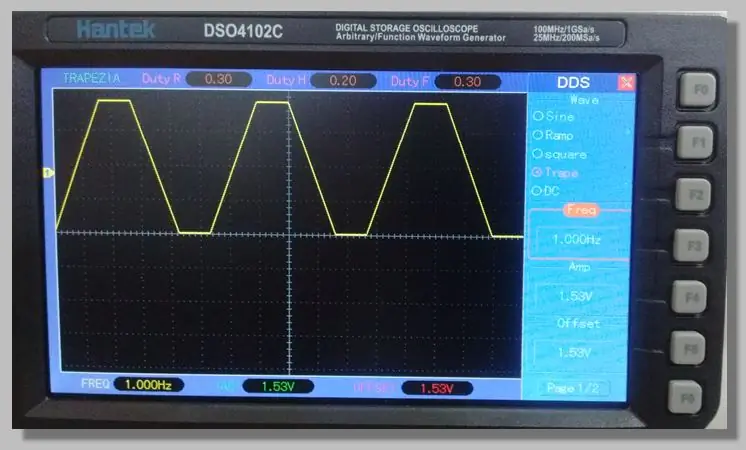
Vi valde en lågfrekvent trapetsformad signal som ger åtkomst till ramperna som går genom hela konverteringsområdet. Detta möjliggör ett stort antal prover på dessa ramper.

Steg 6: Data från Oscilloskopet

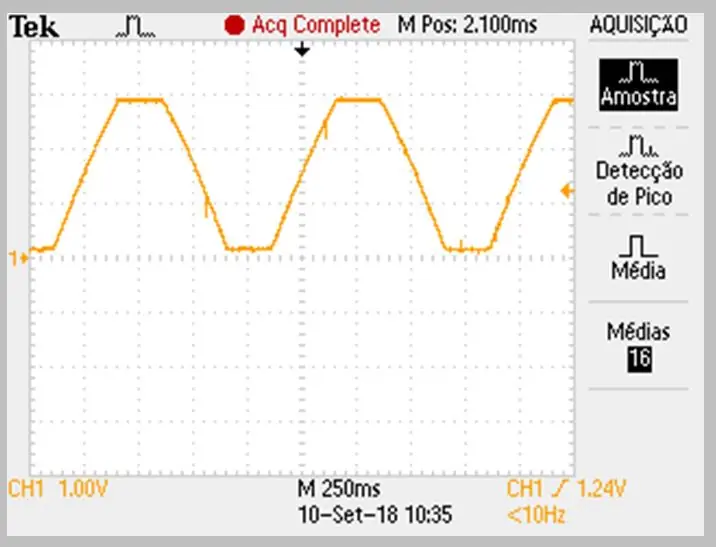
Bilden av fångsten utfördes av oscilloskopet. Data lagrades i en csv -fil. Notera den svaga krökningen på signalens stigande och fallande ramper.

Steg 7: Data erhållna av oscilloskopet (csv -fil i Excel)

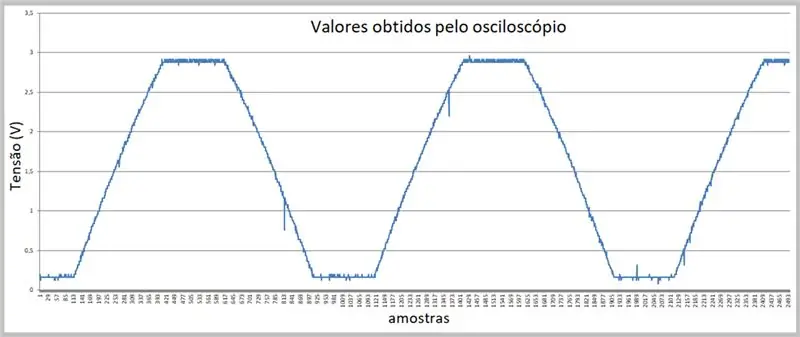
Vi har provtagningarna här.

Steg 8: Data som erhålls av ADC

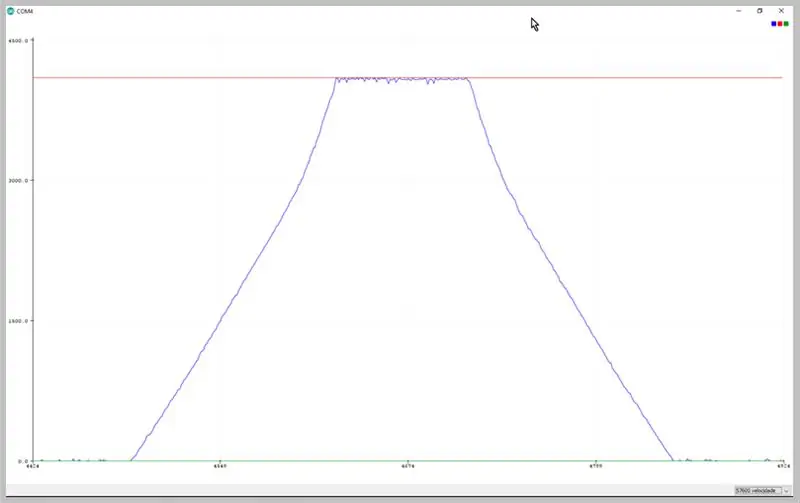
Genom att ändra seriens överföringshastighet kan vi se data som samlas in av ADC. Observera deformationen av den trapetsformade signalen.

Data observerade på Arduino IDE -seriell plotter

Steg 9: Data erhålls av ADC - Excel

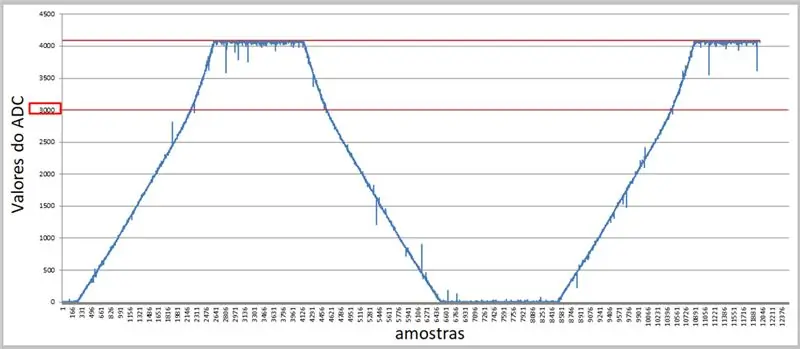
Med en högre hastighet och den seriella terminalen kan vi fånga värdena och tillämpa dem i Excel för våra jämförelser.

Steg 10: Jämförelse av klätterramper

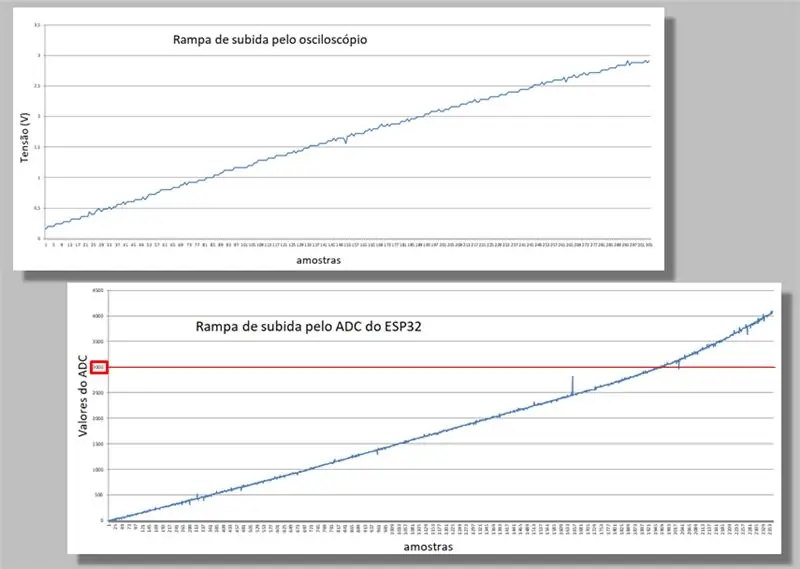
Vi jämför de två klätterramperna för de två fångsterna.

Observera krökning som uppstår på båda ramperna.

Observera också att för samma ramp har vi många fler prover av ESP32 än från oscilloskopet.

Steg 11: Likställa antalet prover

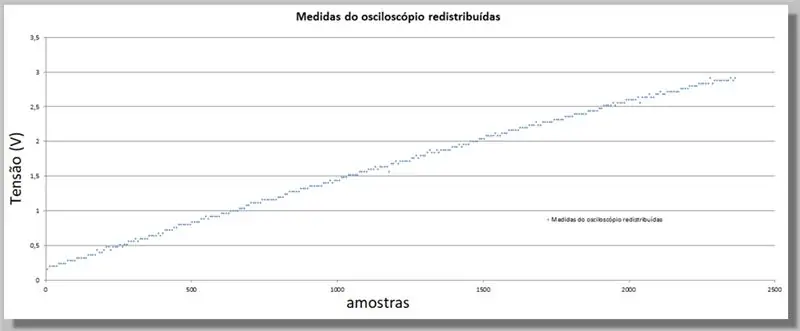
Eftersom ESP32 gav ett större antal prover än oscilloskopet, måste vi jämföra dessa värden, eftersom de kommer att fungera som ett index för att jämföra de två kurvorna.

För detta kommer vi att göra en direkt jämförelse.

Vi har 305 prover för oscilloskoprampen och 2365 prover för ADC -rampen.

Eftersom ramperna har samma intervall kan vi säga att vi har cirka 7,75 prover av ADC för varje oscilloskop.

Multiplicering av indexet för varje oscilloskopprov har samma kurva, men med index som motsvarar ADC och de omfördelade data.

För att fylla i de saknade uppgifterna för de nya positionerna kommer vi att tillämpa en kurva som statistiskt passar de kända uppgifterna.

Steg 12: Fylla i luckorna - trendlinjen

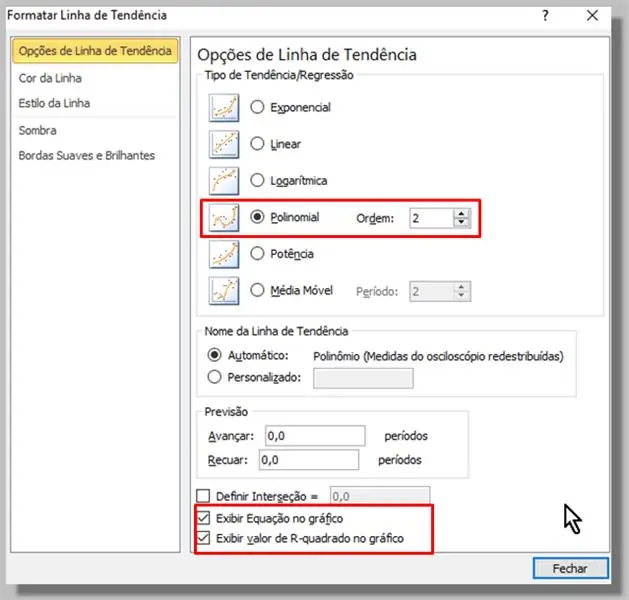
Genom att välja de kända data (blå prickar), genom att klicka och sedan klicka med den högra knappen väljer vi: "Lägg till trendlinje …"

I fönstret som visas väljer vi Polynom -typen (ordning 2 räcker).

Vi kontrollerade också alternativen "Visa ekvation i diagrammet" och "Visa R-kvadratvärde i diagrammet".

Vi klickar på "Stäng".

Steg 13: Fyll i luckorna - grad 2 -polynomkurva

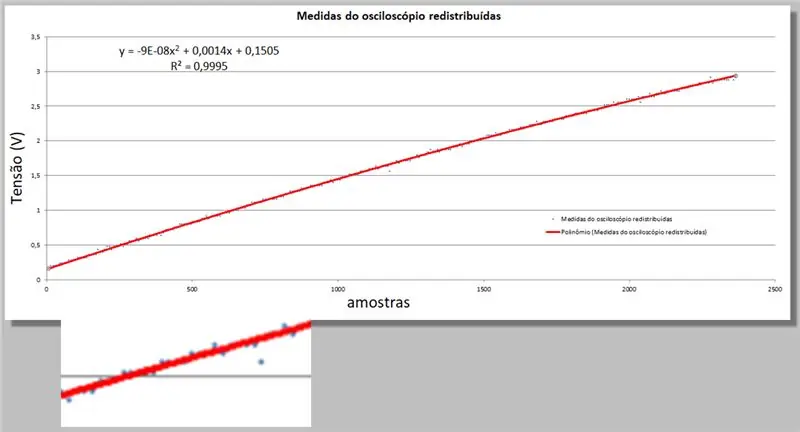
Excel ger oss två nya uppgifter; den andra ordningens ekvation som bäst passar data, och den R-kvadratiska ekvationen som kvantifierar denna tillräcklighet.

Kom bara ihåg att ju närmare 1, desto mer lämplig är ekvationen.

Låt oss inte fördjupa oss i matematiken, låt oss bara använda den som ett verktyg.

Steg 14: Fylla i luckorna - utvärdera funktionen

Låt oss fylla i samplingsluckorna med data som genereras av ekvationen. Och jämför sedan dem punkt för punkt.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Oscilloskopspänning = -9E -08 * index2 + 0, 0014 * index + 0, 1505

Steg 15: Konvertera oscilloskopspänningen till ett ekvivalent värde för att jämföra med ADC

Låt oss dra nytta av detta för att också omvandla värdet på oscilloskopspänningen till ett ekvivalent ADC -värde.

Eftersom det högsta värdet som erhölls i ADP för ESP32 var 4095, vilket motsvarar avläsningen av 2,958V för samma index, kan vi säga att:

Varje volt i oscilloskopets mätningar motsvarar ungefär 1384,4 enheter av AD. Därför kan vi multiplicera alla mätningar av oscilloskopet med detta värde.

Steg 16: Jämför de två ramperna som erhållits

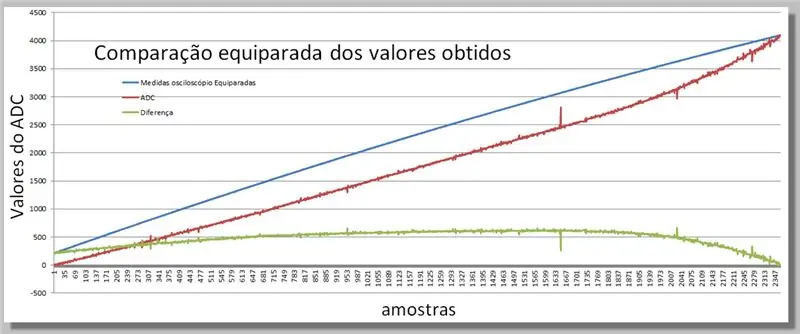
Visualisera skillnaderna som erhålls i de två avläsningarna.

Steg 17: Beteende för ADC -lässkillnaden (ERROR)

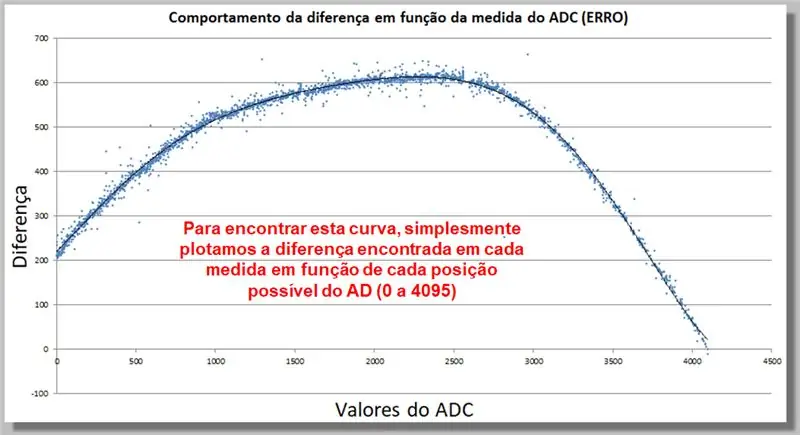
Kurvan nedan visar hur skillnaden i ADC -avläsningen fungerar som en funktion av mätningen. Denna insamling av data gör att vi kan hitta en korrigeringsfunktion.

För att hitta denna kurva plottar vi helt enkelt skillnaden som finns i varje mått som en funktion av varje möjlig AD -position (0 till 4095).

Steg 18: ADC -lässkillnadsbeteende - Hitta en korrigeringsfunktion

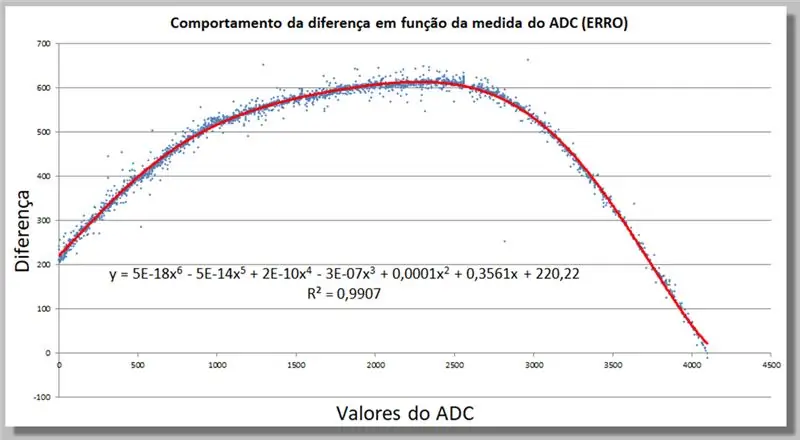
Vi kan bestämma en korrigeringsfunktion i Excel genom att lägga till en trendlinje, nu i högre grad, tills den passar tillräckligt med våra data.

Steg 19: Använda annan programvara

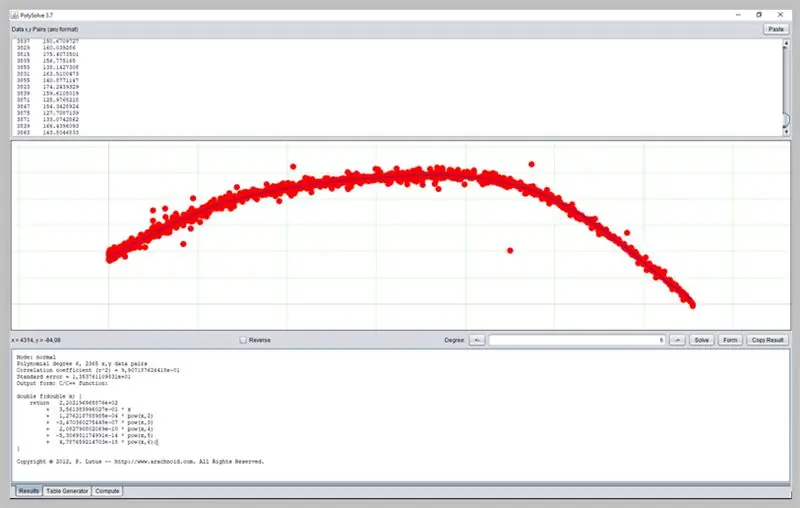
Andra intressanta program för att bestämma kurvor är PolySolve, som kan användas direkt på länken: https://arachnoid.com/polysolve/ eller laddas ner som en Java -applikation.

Det tillåter tillämpning av högre grad polynomregressioner och leverans av den formaterade funktionen, liksom andra funktioner.

För att använda det, ange bara data i den första textrutan. Data måste följa ordningen X, Y åtskilda med ett kommatecken eller flik. Var försiktig när du använder punkten korrekt som decimal.

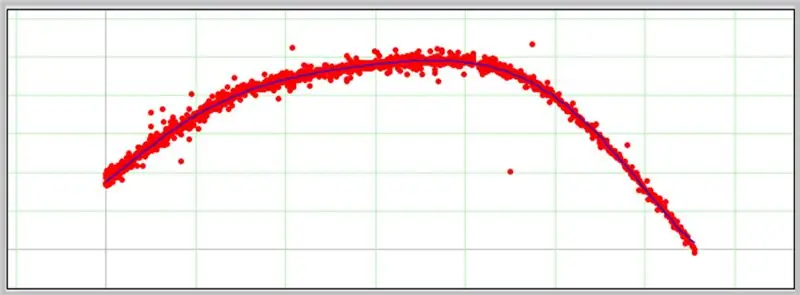
Ett diagram visas i nästa ruta om de inmatade data är korrekt formaterade.

Så här gick vår ADC -felkurva.

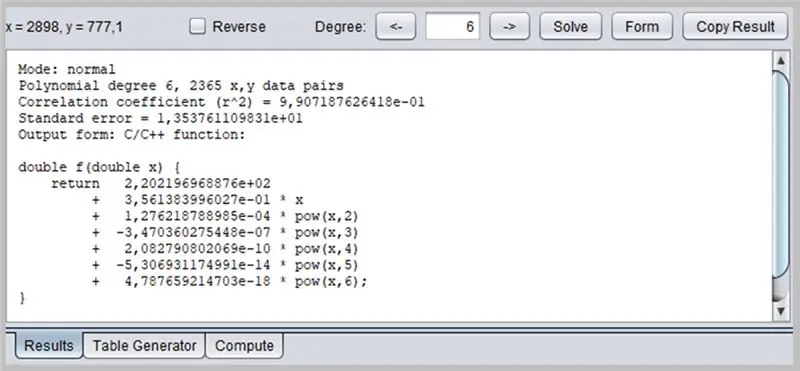
Detta fönster kommer att visa resultatet av regressionen, inklusive funktionstillräcklighetsdata, som i sin tur kan ha sin formatering på flera sätt: som en C / C ++ - funktion, en lista över koefficienter, en funktion skriven i Java, etc.

Obs! Var uppmärksam på decimalavgränsare

Steg 20: Konstanter och inställningar ()

Jag påpekar här GPIO som används för analog inspelning. Jag initierar den seriella porten, liksom stiftet som bestämts för analog inspelning.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente for debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Steg 21: Loop () och korrigeringsfunktionen

Vi registrerar den justerade spänningen och skriver ut värdena med eller utan korrekta korrigeringar.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Lägg märke till i rad 12 att vi har möjlighet att skriva ut data med tillägg av differensfunktionen f (analog_värde).

Steg 22: Använda funktionen PolySolve Correction

Här använder vi PolySolve -funktionen inuti Arduino IDE.

/* Läge: normal polynomgrad 6, 2365 x, y datapar Korrelationskoefficient (r^2) = 9, 907187626418e-01 Standardfel = 1, 353761109831e+01 Utmatningsform: C/C ++-funktion: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Alla rättigheter förbehållna. */ dubbel f (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Notera komma-för-punkt-ändringen som decimalseparator.

Steg 23: Capture With Correction - Plotter Serial

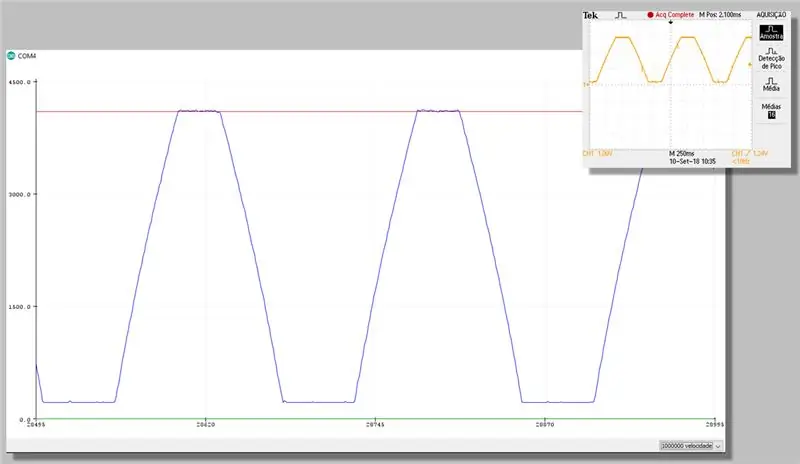
Steg 24: Beräkningskostnad

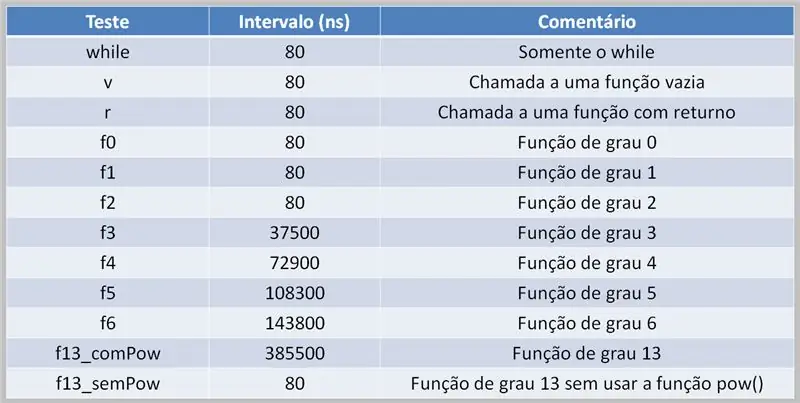
För att utföra polynomberäkningar är det nödvändigt för processorn att hantera denna uppgift. Detta kan leda till förseningar i körningen, beroende på källkoden och tillgänglig datorkraft.

Här ser vi en resultattabell för ett test med flergradiga polynom. Lägg märke till skillnaden mellan tiderna när pow () -funktionen användes och när den inte var det.

Steg 25: Testkod - Setup () och Loop Start ()

Här har vi koden som används i vårt test.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0,0; // contador de chamadas

Steg 26: Testkod - loop () och bearbetning

Jag använde funktionen micros () för att få värdet i mikrosekunder.

// ============== inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

Steg 27: Testkod - Loop () - Resultat

Vi skriver ut värdet som returneras från klass 13 -funktionen med och utan POW för jämförelse, samt behandlingsintervallet.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Steg 28: Testkod - Använda funktioner

Tomma funktioner (endast med retur) av grad 0 och 1.

// FUNÇÃO VAZIDubbel v (dubbel x) {} // FUNÇÃO SOMENTE COM RETORNO dubbel r (dubbel x) {retur x; } // FUNÇÃO DE GRAU 0 dubbel f0 (dubbel x) {retur 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 dubbel f1 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Grade 2, 3 och 4 funktioner.

// FUNÇÃO DE GRAU 2dubbla f2 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 dubbel f3 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 dubbel f4 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4); }

Grade 5 och 6 funktioner.

// FUNÇÃO DE GRAU 5dubbel f5 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 dubbel f6 (dubbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Grade 13 -funktion med hjälp av POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdubbel f13_comPow (dubbel x) {retur 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Grade 13 -funktion utan att använda POW.

// FUNÇÃO DE GRAU SEM USAR O POWdubbel f13_semPow (dubbel x) {retur 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Steg 29: Filer

Ladda ner filerna:

PDF

INO

Kalkylark