Skapa logiska portar i Excel: 11 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:44

Att göra alla 7 grundläggande logikportar i Excel är inte särskilt svårt. Om du förstår funktionerna i Excel skulle det här projektet vara ganska enkelt, om du inte gör det, oroa dig inte, det tar inte lång tid att vänja sig.

Excel skapade redan några logiska grindar för oss men det inkluderar inte alla 7 och vi vill göra det själva ändå.

Projektet tar inte lång tid och när det väl är gjort kan du skapa många kretsar digitalt i Excel.

Steg 1: Vad du behöver

Du behöver inte mycket för detta projekt.

• Dator
• Excel (jag rekommenderar Excel men liknande borde också vara bra)
• Grundläggande kunskap om hur logiska grindar fungerar

Steg 2: Ställ in Excel och Format

Starta först Excel (versionen ska inte spela någon större roll, men jag använde Excel 2016), öppna sedan en ny "Tom arbetsbok".

Gör sedan det format du ser på bilden ovan (På grund av bildens form måste du klicka på den för att se den ordentligt, detta gäller följande bilder). Om du inte kan kopiera formatet läser du följande:

Gör kolumn B & C till en siffra bred, slå ihop rad1 A, B & C.

Skriv sedan in texten.

Steg 3: OCH Gate

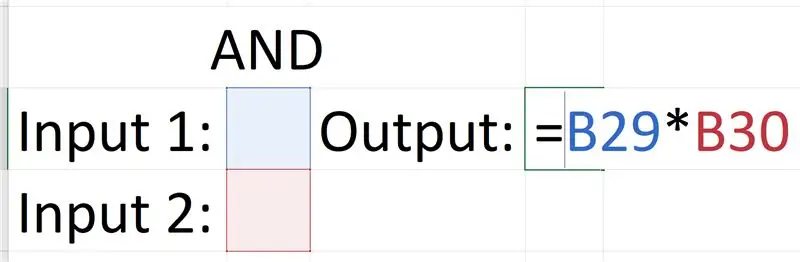
OCH -grinden är den enklaste, det beror på att du kan få utgången genom att bara multiplicera ingångarna.

0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1

Denna produkt av ekvationen är densamma som utgångarna från grinden.

Kopiera formeln och testa den genom att ge den inmatningarna (endast i binär dock).

Kom ihåg att varje gång du skapar en ny grind, kopiera layouten så att inget överlappar varandra.

Steg 4: ELLER Gate

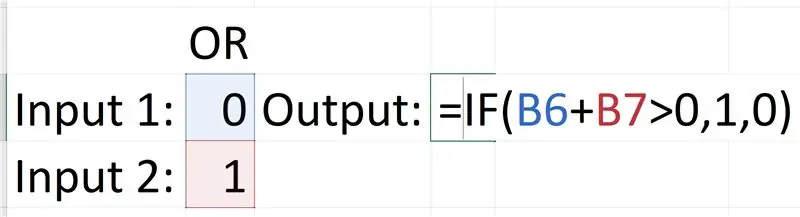
ELLER -grinden är mer komplicerad, det kräver ett 'Om' -uttalande. 'If' -sats fungerar så här: = If (logic_test, [value if true], [value if false]). Det logiska testet vi använder är: Input1 + Input2> 0, det sanna värdet är 1, annars är värdet 0. Detta beror på att endast om båda ingångarna är falska blir utgången falsk, och eftersom 0 + 0 = 0, vad som helst uppsättning ingångar inklusive 1 skulle vara större i värde (summa värde). Så om summan av båda ingångarna är större än 0 så är dess utsättning sant eller 1.

Steg 5: NAND Gate

NAND -grinden är precis som OR -grinden, den kräver ett 'If' -uttalande och logiken bakom den är liknande. Porten ger bara en falsk utgång om båda ingångarna är sanna. Så om vi multiplicerar båda ingångarna kommer en summa som är mindre än 1 att vara sant eftersom 'If' -satsen är: input1 x input2 <1, 1, 0. Om det var förvirrande kan detta diagram hjälpa:

0 x 0 = 0, 0 <1 så True = 1

0 x 1 = 0, 0 <1 så True = 1

1 x 0 = 0, 0 <1 så True = 1

1 x 1 = 1, 1 = 1 så falskt = 0

Steg 6: NOR Gate

NOR -porten använder också en 'If' -sats, satsen för denna gate är: Input1 + Input2 <1, 1, 0. Detta beror på att porten bara ger en True -utgång för båda ingångarna är falska. Eftersom vi lägger till båda ingångarna tillsammans skulle varje uppsättning ingångar inklusive 1 vara större än två 0: or. Då visar sant och falskt påstående att om någon summa är mindre än 1, visar 1 annars 0.

0 + 0 = 0, 0 <1 så True = 1

0 + 1 = 1, 1 = 1 så falskt = 0

1 + 0 = 1, 1 = 1 så falskt = 0

1 + 1 = 2, 2> 1 så falskt = 0

Steg 7: XOR Gate

Detta är ganska likt NOR -porten, men istället för att använda en större eller mindre än symbol använder vi ett likhetstecken eftersom porten bara kommer att ge en True -utgång, den har blandade ingångar, så om vi lägger till båda ingångarna tillsammans, blandade ingångar kommer alltid att ge 1 så vi använder påståendet: Input1 + Input2 = 1, 1, 0.

0 + 0 = 0, 0 ≠ 1 så falskt = 0

0 + 1 = 1, 1 = 1 så True = 1

1 + 0 = 1, 1 = 1 så True = 1

1 + 1 = 2, 2 ≠ 1 så falskt = 0

Steg 8: XNOR Gate

XNOR -porten är ganska enkel, det är i princip motsatsen till XOR -porten, det betyder att logikprovet också är motsatsen. Denna gate ger bara en True -utgång om båda ingångarna har samma nummer, med andra ord är en blandad uppsättning ingångar False. Det logiska testet för XOR -grinden är: Input1 + Input2 = 1, men det logiska testet för XNOR -grinden är: Input1 + Input2 ≠ 1. (är ≠ i Excel -formler).

0 + 0 = 0, 0 ≠ 1 så sant = 1

0 + 1 = 1, 1 = 1 så falskt = 0

1 + 0 = 1, 1 = 1 så falskt = 0

1 + 1 = 2, 2 ≠ 1 så True = 1

Steg 9: NOT Gate

NOT -porten är en enkel gate men dess 'If' -uttalande är precis samma som andra. Den har bara en ingång så du kanske vill ändra ditt format. Porten inverterar bara sin ingång så formeln är inte så svår, logikprovet är: om ingången är 0 och True -satsen är: display 1 annars visar 0.

0 = 0, så sant = 1

1 ≠ 0, så falskt = 0

Steg 10: Digital logikkrets

När du har skapat alla logiska grindar kan du använda dem för att skapa logikkretsar i Excel. Men det nuvarande formatet är för stort så att du kan prova det nya formatet (bilden ovan).

Gör två kolumner en siffra bred, slå ihop de två översta cellerna för att skapa utdata, de två nedre cellerna är ingångar.

När du skriver in formeln skriver du in formeln för den port du vill ha på utmatningsplatsen.

Steg 11: Felsök

Om en logisk grind inte fungerar på något sätt, se till att din formel är korrekt inmatad och att ingångarna är korrekt kopplade till formeln.

Om du är säker på att allt är korrekt kan jag ha gjort ett misstag när jag skrev det här instruerbart. Berätta i så fall för mig i kommentarerna så att jag kan rätta till det.