2-knapps kvadratisk ekvationslösare: 5 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:43

Introduktion

välkommen till min första instruerbara!

Jag startade det här projektet för att utöka mina programmeringskunskaper. Ofta slår du bara ihop olika källkoder för att skapa det program du behöver. Mitt mål var att skriva min egen programkod för att interagera med ett verktyg. Jag gillade att skapa ett enkelt verktyg för beräkning. För någon månad sedan stödde jag en vän för att lösa kvadratisk ekvation.

Bazinga! detta är användningsfallet!

Jag återanvände en gammal metalllåda. Jag föredrog det minimalistiska utseendet och gränssnittet för verktyg. det är anledningen till att jag bara vill använda två knappar för att ge input. Tävlingen kommer att visas med en enkel LCD -skärm.

Tillbehör

Materiallista:

låda

Arkadstil med 2 knappar

Arduino Nano, eller liknande

LCD -skärm 1602 med I2C -adapter

På / Av knapp

trådar

2x 10k Ohm motstånd

batteri 9v block

kontakt för 9v batteri

bakbord

diverse (träbit, metallvinkel, buntband, skruv, brickor)

verktyg:

fick syn på

lödkolv

borrmaskin

dator för programmering

Steg 1: Matematisk bakgrund

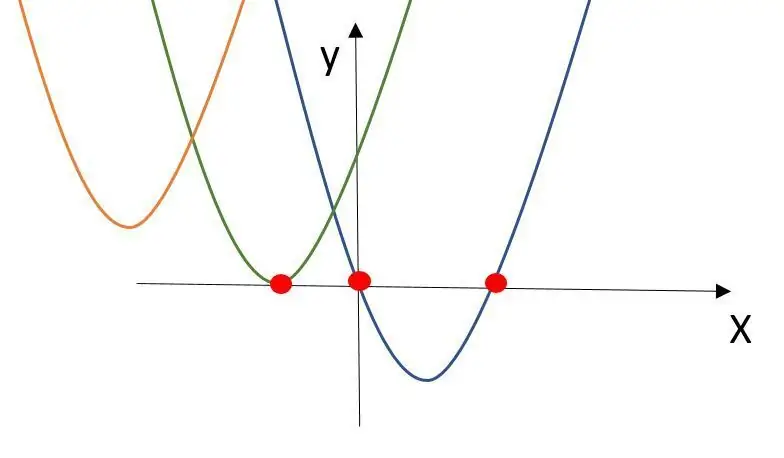
Matematisk bakgrund

Kvadratisk ekvation med 2 knappar visar värdena där den kvadratiska funktionen korsar X-axeln. En kvadratisk funktion kan aldrig korsa X-axeln, en eller två gånger.

Det finns olika sätt att beräkna dessa värden. För mitt verktyg använder jag PQ-formeln (jag är inte säker på om detta uttryck kommer att användas över hela världen).

En kvadratisk ekvation har formen:

ax²+bx+c = 0

För att beräkna korsningspunkterna, dela formen med a x²+px+q = 0 med p = b/a; q = c/a

PQ -formeln:

x1 = -p/2 + sqrt ((p/2) ² -q)

x2 = -p/2 -sqrt ((p/2) ² -q)

Resultatet x kan få 0, 1 eller 2 värden. Det beror på värdet under kvadratroten.

Är värdet> 0, då har PQ-formeln två lösningar.

Är värdet = 0, då har PQ-formeln en lösning

är värdet <0, då har PQ -formeln ingen lösning. Funktionen korsar inte X-axeln.

Steg 2: Programvara

programvara

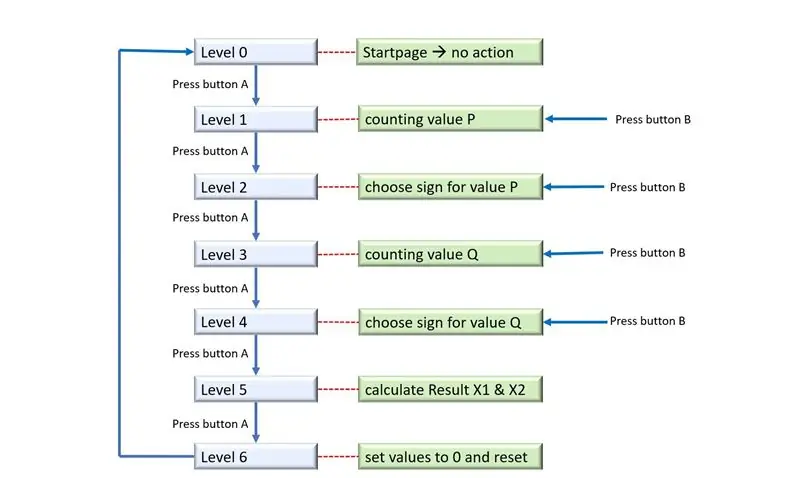
För programmering använde jag den officiella Arduino IDE. Mitt mål var att skapa mitt eget program. Mitt gränssnitt ska ha två knappar. En knapp för att gå mellan olika nivåer, den andra knappen för att ändra värdena på de olika nivåerna.

För att lösa PQ-formeln skapar jag strukturen ovan:

Förvisso, jag uppfinner inte hjulet igen. För att skapa koden använde jag modulen:

- debounce

- display

Följande punkter var de största utmaningarna:

- Hur kan jag välja skylten? Jag löste denna utmaning med funktionen modulo (länk). Koden delar ingången med 2. Är ingången ett udda tal, värdet blir negativt, annars är talet positivt.

- Efter att ha gått igenom alla nivåer måste jag deklarera alla värden till 0.

- Den visade texten raderar bara sändningstecknen. Om koderna skickar ett ord med 4 tecken, laddas bara dessa 4 tecken om. Om ordet innan hade fler tecken, kommer tecknen att stanna. För att åtgärda det kommer den visade texten att fyllas med ämnen. Alla 16 tecken i rad laddas om.

Den slutliga koden bifogas.

Steg 3: Hårdvara

Hårdvara

Delarna listas i ovan. För detta projekt är hårdvaran enkel. Jag behöver bara en Arduino mikroprocessor, 2 knappar och en display. Okej, om du gillar att sätta i en låda behöver du en låda och strömförsörjning också.

Jag återanvänder en gammal metalllåda. Jag borrade ett hål i knappen för att sätta i strömbrytaren för strömförsörjning. Lådkåpan fick 3 hål. Jag borrade två hål för de stora knapparna och skar ett fönster för displayen. Jag sticker en liten träbit bakom locket för att ha fler saker att fixa display och knappar. För att uppgradera utseendet fick rutan klistermärken.

För strömförsörjning rekommenderar jag laddningsbara 9V blockbatterier. Jag ansluter batteriet via strömbrytaren till Arduino. Batteriet sitter fast på lådan med en liten metallvinkel. Anslutningen för batteriet är precis fixerad med buntband.

Mikroprocessorn är en klon av en Arduino nano. För detta användningsfall är prestanda tillräckligt. En Attiny 85, till exempel en Digispark -mikroprocessor, avvisades. Arduino är "brödbrädad" bredvid displayen.

Displayen är en 1602 LCD -skärm. Du kan använda 16 tecken i två rader. Du kan hitta denna display i många olika maskiner och verktyg. Det finns två olika sätt att använda den här skärmen. Du kan ansluta skärmen direkt till styrenheten eller så kan du använda ett tillägg för att kommunicera med displayen via I2C. I2C är ett standardprotokoll. Jag använde det, eftersom det är lättare att ansluta skärmen till styrenheten. Du behöver bara 4 kablar istället för 16, VCC till 5V, GND till GND, SDA till A4, SCL till A5. Displayen fästs med skruvar på lådans lock.

Knapparna är enorma! de har en typisk arkadspelstil. Jag gillar det! Knapparna är anslutna till digital stift 4 och 7. Glöm inte 10K -resistorerna!

För att öppna locket, till exempel för att byta batteri, använde jag längre kablar anslutna till brödbrädet.

Steg 4: Kabeldragning

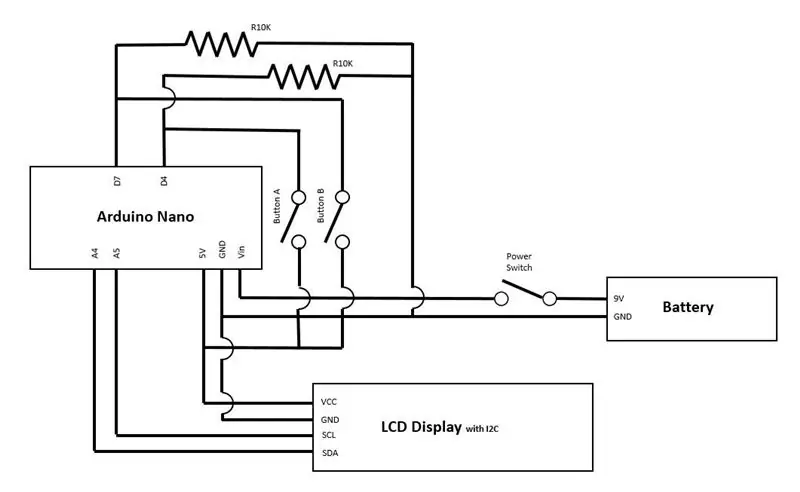
Steg 5: Framtidsförbättring

Framtidsförbättring

När du har avslutat ett projekt hittar du alltid buggar eller funktioner som kan förbättras. I det här projektet är jag glad att bara hitta några punkter, jag skulle förbättra för framtiden.

För nästa gång skulle jag förbättra exploateringen i rutan. Jag fixade displayen, strömbrytaren och knapparna i början av detta projekt. I slutet fick jag lite problem med att hitta tillräckligt med utrymme för batteriet och mikroprocessorn i lådan. När jag satte knappen och displayen mer utanför skulle jag inte ha några problem med utrymmet för delarna inuti lådan.

För närvarande har jag inget användningsfall för att lösa kvadratisk ekvation. För att förbättra verktyget skulle jag vilja utöka verktyget med ytterligare matematiska saker, till exempel grundläggande kalkyl eller formler som binominell formel eller mening i Pythagoras.