
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:37.
- Senast ändrad 2025-01-23 15:10.


Här är en praktisk tillämpning av komplexa matematiska ekvationer.
Detta är faktiskt en mycket användbar teknik som du kan använda för att karakterisera komponenter, eller till och med en antenn, vid förutbestämda frekvenser.
Om du har pysslat med elektronik kanske du känner till resistorer och Ohms lag. Dvs. R = V / I Du kan nu bli förvånad över att veta att detta är allt du behöver lösa för komplexa impedanser också! Alla impedanser är i huvudsak komplexa, det vill säga de har en verklig och en imaginär del. I fallet med en motstånd är den imaginära (eller reaktansen) 0, motsvarande finns det ingen fasskillnad mellan V och I, så vi kan utelämna dem.
En snabb sammanfattning om komplexa tal. Komplex betyder helt enkelt att talet består av två delar, en verklig och en imaginär. Det finns två sätt att representera komplexa tal, till exempel i figuren ovan kan en punkt definieras av de verkliga och imaginära värdena, till exempel var de gula och blå linjerna möts. Till exempel om den blå linjen var vid 4 på X -axeln och 3 på Y -axeln, skulle detta tal vara 4 + 3i, i indikerar att detta är den imaginära delen av detta tal. Ett annat sätt att definiera samma punkt skulle vara längden (eller amplituden) på den röda linjen samt vilken vinkel den gör med horisontalen. I exemplet ovan skulle detta vara 5 <36,87.
Eller en linje med en längd av 5 i en vinkel på 36,87 grader.
I ekvationen framför alla parametrar kan R, V och I anses ha en imaginär del, när man arbetar med motstånd är detta värde 0.
När du arbetar med induktorer eller kondensatorer, eller när en fasskillnad kan mätas (i grader) mellan signalerna, förblir ekvationen densamma men den imaginära delen av talet måste inkluderas. De flesta vetenskapliga räknare gör det mycket enkelt att arbeta med komplex matematik. I den här självstudien kommer jag att arbeta igenom ett exempel på en Casio fx-9750GII.
Först en sammanfattning av motståndsspänningsdelarens ekvation.
Enligt figuren -
Spänningen vid Y är ström i multiplicerad med R2
i är spänning X dividerat med summan av R1 och R2
När R2 är okänd kan vi mäta de andra värdena, X, Y, R1 och ordna om ekvationen som ska lösas för R2.
Tillbehör
Vetenskaplig kalkylator
Signalgenerator
Oscilloskop
Steg 1: Inställning

Låt oss anta att vi vill beräkna induktansen för Device Under Test (DUT) vid 1 MHz.
Signalgeneratorn är konfigurerad för en sinusformad utgång på 5V vid 1MHz.
Vi använder 2k ohm motstånd, och oscilloskopskanalerna är CH1 och CH2
Steg 2: Oscilloskop

Vi får vågformerna som visas i figuren. Ett fasskifte kan ses och mätas på oscilloskopet för att leda med 130ns. Amplituden är 3,4V. Observera att signalen på CH1 ska vara 2,5V eftersom den tas vid spänningsdelarens utgång, här visas den som 5V för tydlighetens skull, eftersom detta är värdet vi också måste använda i våra beräkningar. dvs 5V är ingångsspänningen till avdelaren med den okända komponenten.
Steg 3: Beräkna fas

Vid 1MHz är insignalens period 1us.
130ns ger ett förhållande på 0,13. Eller 13%. 13% av 360 är 46,6
5V -signalen ges en vinkel på 0.. eftersom detta är vår insignal och fasförskjutning är relativt den.
3,4V -signalen ges vinkeln +46,6 (+ betyder att den leder, för en kondensator skulle vinkeln vara negativ).
Steg 4: På räknaren


Nu anger vi helt enkelt våra mätvärden i miniräknaren.
R är 2k
V är 5 (EDIT - V är 5, senare i ekvationen används X! Resultatet är exakt samma som jag har X som 5 i min räknare)
Y är vår uppmätta spänning med fasvinkeln, detta nummer anges som ett komplext tal, helt enkelt genom att ange vinkeln som visas på kalkylatorskärmen
Steg 5: Lös ekvationen

nu ekvationen
(Y * R) / (X - Y)
skrivs in i miniräknaren, är detta exakt samma ekvation som vi använder för att lösa resistorspänningsdelare:)
Steg 6: Beräknade värden


Kalkylatorn gav resultatet
18 + 1872i
18: an är den verkliga delen av impedansen och den har en induktans på +1872 vid 1MHz.
Vilket fungerar till 298uH enligt induktorimpedansekvationen.
18 ohm är högre än motståndet som skulle mätas med en multimeter, detta beror på att multimetern mäter motstånd vid DC. Vid 1MHz finns det hudeffekt, där ledarens inre del kringgås av strömmen och den bara flyter på utsidan av koppar, vilket effektivt minskar ledarens tväryta och ökar dess motstånd.
Rekommenderad:
Raspberry Pi Box med kylfläkt med CPU -temperaturindikator: 10 steg (med bilder)

Raspberry Pi Box med kylfläkt med CPU-temperaturindikator: Jag hade introducerat hallon pi (nedan RPI) CPU-temperaturindikeringskrets i det föregående projektet. Kretsen visar helt enkelt RPI 4 olika CPU-temperaturnivå enligt följande.- Grön lysdiod tänds när CPU -temperaturen ligger inom 30 ~
Spel med 4 knappar med en analog ingång: 6 steg (med bilder)

Spel med 4 knappar med en analog ingång: Denna instruerbara funktion fokuserar på att använda en analog ingångslinje för flera knappar som kan detekteras oberoende av varandra. Och för att markera användningen av dessa knappar ingår programvara för att spela fyra olika spel med 4 knappar. Alla spel (8 tum
Plattform med oändliga nivåer på GameGo med Makecode Arcade: 5 steg (med bilder)

Plattform med oändliga nivåer på GameGo med Makecode Arcade: GameGo är en Microsoft Makecode -kompatibel bärbar konsol för retrospel som utvecklats av TinkerGen STEM -utbildning. Det är baserat på STM32F401RET6 ARM Cortex M4 -chip och gjord för STEM -lärare eller bara människor som gillar att ha roligt med att skapa retro -videospel
Akustisk levitation med Arduino Uno Steg-för-steg (8-steg): 8 steg

Akustisk levitation med Arduino Uno Steg-för-steg (8-steg): ultraljudsgivare L298N Dc kvinnlig adapter strömförsörjning med en manlig DC-pin Arduino UNOBreadboardHur det fungerar: Först laddar du upp kod till Arduino Uno (det är en mikrokontroller utrustad med digital och analoga portar för att konvertera kod (C ++)
Trådlös fjärrkontroll med 2,4 GHz NRF24L01 -modul med Arduino - Nrf24l01 4 -kanals / 6 -kanals sändarmottagare för Quadcopter - Rc helikopter - RC -plan med Arduino: 5 steg (med bi
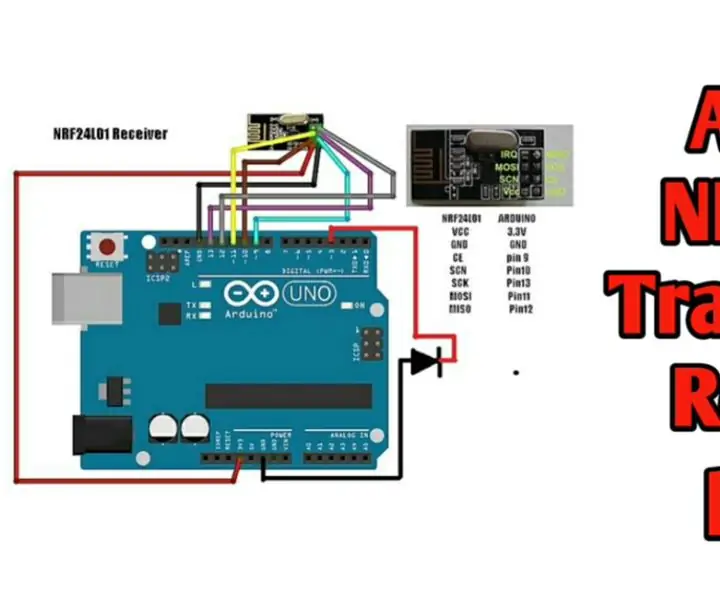
Trådlös fjärrkontroll med 2,4 GHz NRF24L01 -modul med Arduino | Nrf24l01 4 -kanals / 6 -kanals sändarmottagare för Quadcopter | Rc helikopter | Rc -plan med Arduino: Att driva en Rc -bil | Quadcopter | Drone | RC -plan | RC -båt, vi behöver alltid en mottagare och sändare, antag att för RC QUADCOPTER behöver vi en 6 -kanals sändare och mottagare och den typen av TX och RX är för dyr, så vi kommer att göra en på vår
