Lösa sanningstabeller: 10 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:38

En sanningstabell är ett sätt att visualisera alla resultat av ett problem. Denna instruktionsuppsättning är gjord för människor som kommer igång med diskret matematik. Vi kommer att träna idag med ett exempelproblem som är specifikt för dessa instruktioner. Du behöver lite skrappapper och en penna för att visualisera bordet. Detta problem bör ta cirka 5 minuter att slutföra för personer med förkunskaper om ämnet och cirka 10 minuter för nybörjare.

För denna instruktionsuppsättning kommer vi att fokusera på problemet ~ p Λ q. Vi använder detta för att introducera några symboler som behövs för att tolka sanningstabeller.

Steg 1: Förstå sanningstabeller

Ett sanningstabell är ett sätt att visualisera alla problemets möjligheter. Att känna till sanningstabeller är en grundläggande nödvändighet för diskret matematik. Här hittar vi alla resultat för den enkla ekvationen ~ p Λ q.

Steg 2: Att känna till symbolerna

Det första steget till sanningstabellen är att förstå tecknen. "~" I detta problem står för negation. "P" och "q" är båda variabler. "Λ" motsvarar "och". Denna ekvation läses som "inte p och q", vilket betyder att ekvationen är sann om p inte är sant och q är sant.

Steg 3: Formatera tabellen

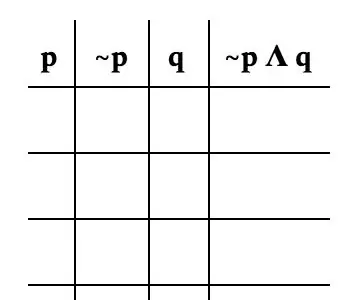
Nu för att bilda det faktiska bordet. Det är viktigt att dela upp problemet med varje variabel. För detta problem kommer vi att dela upp det enligt följande: p, ~ p, q och ~ p Λ q. Bilden är ett bra exempel på hur ditt bord ska se ut.

Steg 4: Tilldela sant och falskt

Eftersom det bara finns två variabler kommer det bara att finnas fyra möjligheter per variabel. För p delar vi upp det med hälften av mellanslag som tas av T (för sant) och den andra halvan av F (för falskt).

Steg 5: Negation

För ~ p skriver du motsatt tecken som p har eftersom ~ p är motsatsen till p.

Steg 6: Variabel "q"

För q växlar du mellan T och F för att få varje möjlig kombination. Eftersom ekvationen endast fokuserar på ~ p, kan vi ignorera p -kolumnen när jag bestämmer ekvationens sanning. Symbolen “Λ” betyder att både ~ p och q måste vara sanna för att ekvationen ska vara sann.

Steg 7: Lösa för falskt i den sista kolumnen

För den första raden, eftersom ~ p är F och q är T, ~ p Λ q är F i scenariot som ~ p är F och q är T. Det enda scenariot som ekvationen är T är där ~ p är T och q är T.

Steg 8: Hitta det sanna i den senaste kolumnen

Detta betyder att den enda raden som är T är den tredje.

Steg 9: Avsluta tabellen

Dubbelkolla att ditt bord är korrekt. Du gör detta genom att kontrollera att dina tecken är rätt och se till att den sista kolumnen är korrekt gjord. Den sista kolumnen är resultatet av alla möjliga permutationer från variablerna.

Steg 10: Klar

Nu när du vet hur du gör ett grundläggande sanningstabell, fortsätt träna! Ju mer du tränar, desto bättre blir du på att göra dem.