Rinnande medelvärde för dina mikrokontrollerprojekt: 6 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:38

I den här instruktionsboken kommer jag att förklara vad ett löpande medelvärde är och varför du bör bry dig om det, samt visa dig hur det ska implementeras för maximal beräkningseffektivitet (oroa dig inte om komplexiteten, det är väldigt enkelt att förstå och jag kommer att ge också ett lättanvänt bibliotek för dina arduino -projekt:)

Rinnande medelvärde, även vanligtvis kallat glidande medelvärde, glidande medelvärde eller löpande medelvärde, är en term som används för att beskriva medelvärdet för de sista N -värdena i dataserier. Det kan beräknas precis som normalt genomsnitt eller så kan du använda ett knep för att få en minimal inverkan på kodens prestanda.

Steg 1: Use Case: Utjämning av ADC -mätningar

Arduino har en anständig 10 bitars ADC med väldigt lite brus. När man mäter värdet på en sensor som potentiometer, fotoresistor eller andra högbrusskomponenter är det svårt att lita på att mätningen är korrekt.

En lösning är att göra flera mätningar varje gång du vill läsa din sensor och genomsnittliga dem. I vissa fall är detta en hållbar lösning men inte alltid. Om du ville läsa ADC 1000 gånger per sekund, skulle du behöva 10 000 om du i genomsnitt tog 10 mätningar. Ett stort slöseri med beräkningstid.

Min föreslagna lösning är att ta mätningar 1000 gånger i sekunden, uppdatera löpande genomsnitt varje gång och använda det som aktuellt värde. Denna metod introducerar viss latens men minskar beräkningskomplexiteten i din applikation, vilket ger dig mycket mer tid för ytterligare bearbetning.

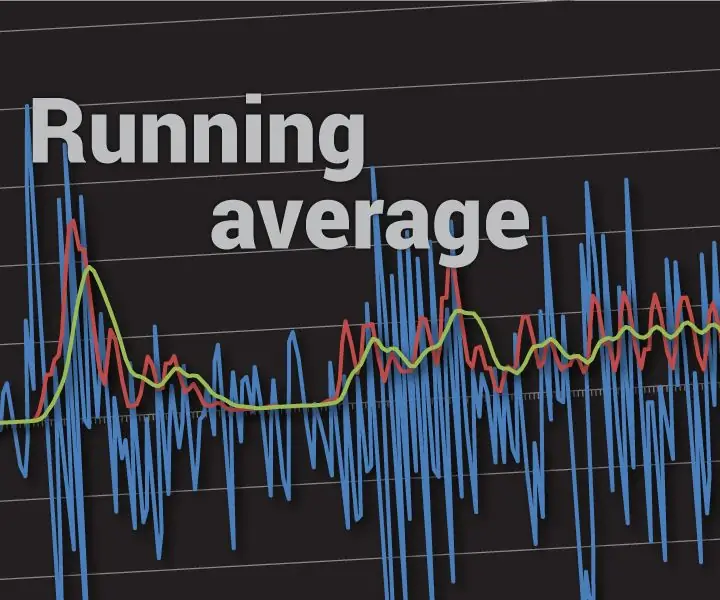
På bilden ovan använde jag löpande medelvärde för de senaste 32 mätningarna. Du kommer att se att denna metod inte är 100% felsäker men den förbättrar noggrannheten avsevärt (det är inte värre än att i genomsnitt ta 32 prover varje gång). Om du ville beräkna i genomsnitt 32 mätningar varje gång, skulle det ta över 0,25 ms på Arduino UNO bara för mätningar!

Steg 2: Användningsfodral: Mätning av DC -komponent i mikrofonsignal

Arduino kan mäta spänningar mellan 0 och Vcc (normalt 5 V). Ljudsignalen är helt AC och om du vill mäta den på en mikrokontroller måste du förspänna den runt 1/2 Vcc. I ett Arduino UNO -projekt skulle det innebära ungefär 2,5 V (DC) + ljudsignal (AC). När du använder 10 bitars ADC och 5 V strömförsörjning, bör 2,5 V bias vara lika med mätningen 512. Så för att få ett AC -värde för signalen bör 512 subtraheras från ADC -mätningen och det är det, eller hur?

I en idealvärld skulle det vara sant. Tyvärr är det verkliga livet mer komplicerat och vår signalfördom tenderar att glida. Mycket vanligt är 50 Hz brus (60 Hz om du bor i USA) från elnätet. Vanligtvis är det inte alltför problematiskt men det är bra att veta att det finns. Mer problematiskt är linjär drift från uppvärmning av komponenter. Du ställer noggrant in DC -offset -korrigering vid start och det försvinner långsamt bort när din applikation körs.

Jag kommer att illustrera detta problem med en (musik) beat -detektor. Du ställer in din bias -borttagning och slag är tydliga (bild 2). Efter en tid rör sig DC -förspänning och slag är knappt märkbara för mikrokontrollern (bild 3). Slagdetekteringsalgoritm kommer att undersökas på djupet i en framtida instruerbar, eftersom den överskrider tillämpningsområdet för denna artikel.

Lyckligtvis finns det ett sätt att ständigt beräkna ljudets DC -förskjutning. Det kommer inte som någon överraskning att löpande medel, ämnet för detta instruerbara, ger en lösning.

Vi vet att medelvärdet för alla växelströmsignaler är 0. Med hjälp av denna kunskap kan vi dra av det genomsnittliga värdet för växelström+likströmssignal är att det är likström. För att ta bort det kan vi ta ett löpande genomsnitt av de senaste värdena och subtrahera det från nuvarande ADC -avläsning. Observera att du måste använda ett tillräckligt långt löpande medelvärde. För ljud, en tiondel av en sekund (antal samplingar beror på din samplingshastighet) borde räcka men vet att längre medelvärden fungerar bättre. På första bilden kan du se exempel på verklig DC -förspänningsberäkning med löpande medelvärde med 64 element vid 1 kHz samplingshastighet (mindre än jag rekommenderade men det fungerar fortfarande).

Steg 3: Beräkning

Du kan tänka dig att köra genomsnittet som en genomsnittlig vikt för människor i läkarens väntrum. Läkaren avslutar undersökningen av en patient och samtidigt går en ny in i väntrummet.

För att ta reda på medelvikten för alla väntande patienter i väntrummet kan sjuksköterskan sedan fråga varje patient om deras vikt, lägga till dessa siffror och dividera med antalet patienter. Varje gång läkaren accepterar en ny patient skulle sjuksköterskan upprepa hela processen.

Du kanske tänker: "Det här låter inte alltför effektivt … Det måste finnas ett bättre sätt att göra detta." Och du skulle ha rätt.

För att optimera denna process kan sjuksköterskan föra ett register över den totala vikten för den aktuella patientgruppen. När läkaren kallar in ny patient kommer sjuksköterskan att fråga honom om hans vikt och subtrahera den från gruppsumman och låta honom gå. Sjuksköterskan skulle sedan fråga patienten som precis gick in i väntrummet om sin vikt och lägga till den i totalen. Medelvikten för patienterna efter varje skift skulle vara summan av vikter dividerat med antalet patienter (ja, samma som tidigare men nu frågade sjuksköterskan bara två personer om deras vikt istället för dem alla). Jag inser att detta stycke kan ha varit lite förvirrande så se illustrationen ovan för ytterligare klarhet (eller ställ frågor i kommentarer).

Men även om du inte tyckte att det sista stycket var förvirrande kan du ha frågor som vad som borde finnas i ackumulator i början, hur lägger jag det jag just läste i en verklig C -kod? Det kommer att tas upp i nästa steg, där du också får min källkod.

Steg 4: Koden

För att beräkna löpande medelvärde måste du först lagra de sista N -värdena. du kan ha en array med N -element och flytta hela innehållet en plats varje gång du lägger till ett element (snälla gör inte det här), eller du kan skriva över ett gammalt element och justera pekaren till nästa element som ska slängas ut (gör det här:)

Ackumulator bör börja initialiseras till 0, samma gäller för alla element i fördröjningslinjen. I andra fall kommer ditt löpande medelvärde alltid att vara fel. Du kommer att se att delayLine_init tar hand om att initiera fördröjningslinjen, du bör ta hand om ackumulator själv.

Att lägga till ett element i fördröjningslinjen är lika enkelt som att minska indexet för det nyaste elementet med 1, så att det inte pekar ut på sidan av fördröjningslinjmatrisen. efter att indexet har minskat när det är 0, kommer det att gå runt till 255 (eftersom det är ett 8 -bitars osignerat heltal). Modulo (%) -operatör med storleken på fördröjningslinjesystemet kommer att säkerställa att index pekar på ett giltigt element.

Att beräkna ett löpande medelvärde bör vara lätt att förstå om du följde min analogi i föregående steg. Subtrahera det äldsta elementet från ackumulatoren, lägg till det senaste värdet i ackumulatoren, tryck det senaste värdet till fördröjningslinjen, returnera ackumulatorn dividerat med antalet element.

Lätt, eller hur?

Experimentera gärna med att använda den bifogade koden för att bättre förstå hur allt detta fungerar. Som det ser ut för närvarande läser arduino analogt värde på analog pin A0 och skriver ut "[ADC -värde], [körmedelvärde]" på seriell port med 115200 baudhastighet. Om du öppnar arduinos seriella plotter med rätt överföringshastighet ser du två rader: ADC -värde (blått) och utjämnat värde (rött).

Steg 5: Extra

Det finns några saker som du inte nödvändigtvis behöver veta för att använda löpande medelvärde i ditt projekt utan att skada att veta.

fördröjning: Jag börjar med att tala om illustrationen av detta steg. Du kommer att märka att löpande medelvärde för fler element medför större fördröjning. Om din svarstid för att ändra värde är avgörande, kanske du vill använda kortare löpande medelvärde eller öka samplingsfrekvensen (mät oftare).

Gå vidare.

initialisering: När jag pratade om att initiera ackumulator och fördröjningselement sa jag att du bör initialisera dem alla till 0. Alternativt kan du initiera fördröjningslinjen till allt du vill, men ackumulatoren ska börja som en summa av de nyaste N -elementen i fördröjningslinjen (där N är antalet element i ditt löpande medelvärde). Om ackumulator startar som något annat värde blir det beräknade genomsnittet fel - antingen för lågt eller för högt, alltid med samma belopp (förutsatt samma initiala förhållanden). Jag föreslår att du försöker lära dig varför det är så genom att använda "penna och pappersimulering".

ackumulatorstorlek: Du bör också notera att ackumulatoren ska vara tillräckligt stor för att lagra summan av alla element i fördröjningslinjen om de alla är positiva eller negativa max. I praktiken betyder det att ackumulator ska vara en datatyp större än fördröjningslinjeelement och signerad om fördröjningslinjeelement är signerade.

trick: Långa fördröjningslinjer tar upp mycket minne. Det kan snabbt bli ett problem. Om du är mycket minnesbegränsad och inte bryr dig så mycket om noggrannhet kan du närma dig löpande medelvärde genom att helt utelämna fördröjning och göra detta istället: subtrahera 1/N * ackumulator från ackumulator och lägg till nytt värde (på exempel på 8 långa genomsnitt: ackumulator = ackumulator * 7/8 + newValue). Denna metod ger fel resultat men det är en anständig metod för att beräkna löpande medelvärde när du har slut på minne.

lingvistik: "löpande medelvärde/medelvärde" används vanligtvis när man hänvisar till realtidsmedelvärde medan "glidande medelvärde/medelvärde" vanligtvis betyder att algoritmen körs på statiska datamängder som Excel -kalkylblad.

Steg 6: Slutsats

Jag hoppas att denna instruerbara var lätt att förstå och att den kommer att hjälpa dig i dina framtida projekt. Ställ gärna frågor i kommentarerna nedan om det är något oklart.