Kvantimetrisk bildbehandling: 5 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:46

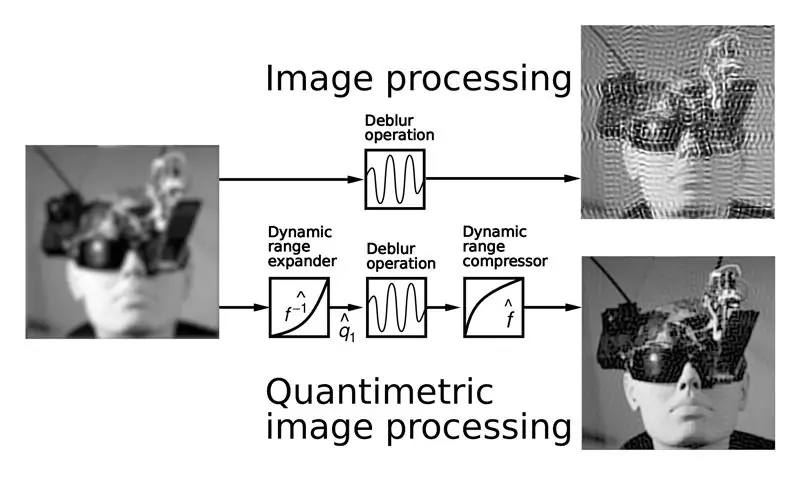
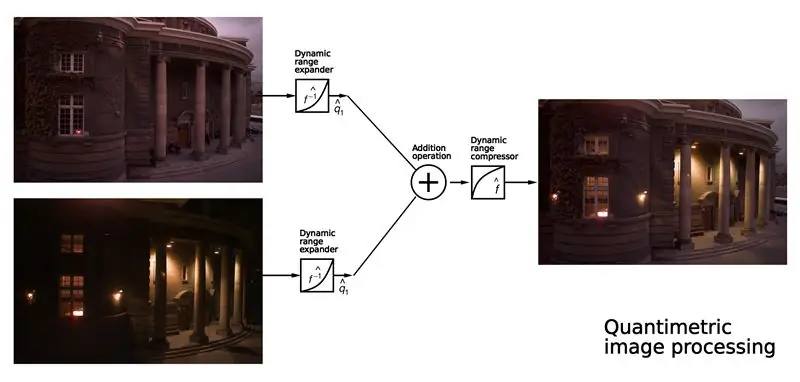
(Figuren ovan illustrerar jämförelse av befintlig bildbehandlingsmetod med kvantimetrisk bildbehandling. Notera det förbättrade resultatet. Bilden uppe till höger visar konstiga artefakter som kommer från felaktigt antagande att bilder mäter något som ljus. Bilden längst ner till höger visar bättre resultat genom att göra samma sak kvantimetriskt.)

I denna instruktionsbok lär du dig hur du kraftigt kan förbättra prestanda för befintliga bild- eller synavkännande system genom att använda ett mycket enkelt koncept: Kvantimetrisk bildavkänning

Kvantimetrisk bildbehandling förbättrar kraftigt något av följande:

• Befintlig bildbehandling som bildskärpning;
• Maskininlärning, datorsyn och mönsterigenkänning;
• Bärbar ansiktsigenkänning (se https://wearcam.org/vmp.pdf), AI och HI -baserad vision, etc.

Grundtanken är att kvantimetriskt förbehandla och efterbehandla bilderna enligt följande:

1. Utöka bildens eller bildernas dynamiska omfång;
2. Bearbeta bilden eller bilderna som du normalt skulle göra;
3. Komprimera bildens eller bildernas dynamiska omfång (dvs. ångra steg 1).

I tidigare instruktioner lärde jag mig några aspekter av HDR (High Dynamic Range) avkänning och kvantimetrisk avkänning, t.ex. linjäritet, superposition, etc.

Låt oss nu använda denna kunskap.

Ta en befintlig process som du vill använda. Exemplet jag visar är bildskärmning, men du kan också använda det för nästan allt annat.

Steg 1: Utöka det dynamiska intervallet för din bild eller dina bilder

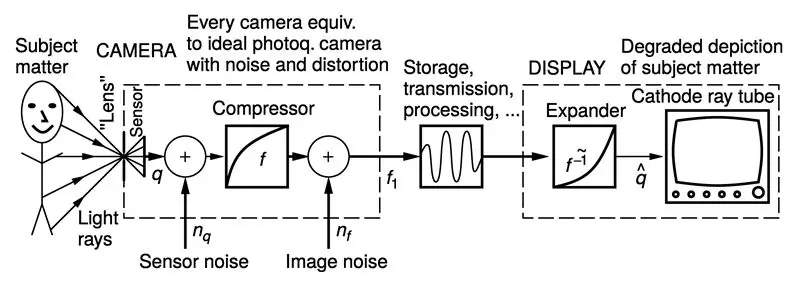
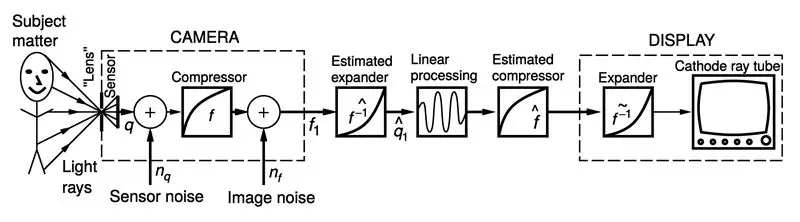
(Figurer anpassade från "Intelligent Image Processing", John Wiley and Sons Interscience Series, Steve Mann, november 2001)

Det första steget är att utöka det dynamiska intervallet för inmatningsbilden.

Helst bör du först bestämma kamerans svarsfunktion, f, och sedan applicera det inversa svaret, f invers, på bilden.

Typiska kameror är komprimerade för dynamiskt omfång, så vi vill vanligtvis använda en expansiv funktion.

Om du inte känner till svarsfunktionen, börja med att prova något enkelt som att ladda bilden till en bildmatris, casta variablerna till en datatyp som (float) eller (double) och höja varje pixelvärde till en exponent, till exempel som att kvadrera varje pixelvärde.

Logisk grund:

Varför gör vi det här?

Svaret är att de flesta kameror komprimerar sitt dynamiska omfång. Anledningen till att de gör detta är att de flesta displaymedier utökar dynamiskt omfång. Detta är helt av en slump: mängden ljus som avges från en katodstrålerörs-tv-skärm är ungefär lika med spänningen som höjs till exponenten 2,22 så att när videospänningsingången är ungefär halvvägs är mängden ljus som avges mycket mindre än hälften.

Fotografiska medier är också expansiva med dynamiskt intervall. Till exempel avger ett fotografiskt "neutralt" grått kort 18% av infallande ljus (inte 50% av infallande ljus). Detta mycket ljus (18%) anses vara mitt i svaret. Så som du kan se, om vi tittar på en graf med utdata som en funktion av inmatning, uppträder skärmmedia som om de är idealiska linjära skärmar som innehåller en dynamisk räckviddsexpander före det ideala linjära svaret.

I den översta figuren ovan kan du se displayen inramad med en prickad linje, och det motsvarar att ha en expander före den idealiska linjära displayen.

Eftersom skärmar i sig är expansiva måste kameror vara utformade så att de är kompressiva så att bilderna ser bra ut på de befintliga skärmarna.

Förr i tiden när det fanns tusentals tv -mottagarskärmar och bara en eller två sändningsstationer (t.ex. bara en eller två tv -kameror) var det en lättare lösning att sätta in en komprimerad olinearitet i kameran än att återkalla alla tv -apparater och sätt en i varje tv -mottagare.

Av en slump hjälpte detta också till bullerdämpning. I ljud kallar vi detta "Dolby" ("companding") och ger patent för det. I video hände det helt av en slump. Stockham föreslog att vi skulle ta logaritmen för bilder innan vi behandlar dem och sedan ta antiloggen. Vad han inte insåg är att de flesta kameror och skärmar redan gör detta helt av en slump. I stället är det jag föreslog att vi gör raka motsatsen till vad Stockham föreslog. (Se "Intelligent bildbehandling", John Wiley and Sons Interscience Series, sidan 109-111.)

På den nedre bilden ser du den föreslagna antihomomorfa (kvantimetriska) bildbehandlingen, där vi har lagt till steget för expansion och komprimering av det dynamiska området.

Steg 2: Bearbeta bilderna eller utför datorsyn, maskininlärning eller liknande

Det andra steget, efter expansion av dynamiskt område, är att bearbeta bilderna.

I mitt fall utförde jag helt enkelt en dekonvolution av bilden, med suddningsfunktionen, dvs bildskärpning, som är allmänt känt inom teknikens ståndpunkt.

Det finns två stora kategorier av kvantimetrisk bildavkänning:

• Att hjälpa människor att se;
• Hjälp maskiner att se.

Om vi försöker hjälpa människor att se (vilket är exemplet jag visar här) är vi inte klara ännu: vi måste ta tillbaka det bearbetade resultatet till bildytan.

Om vi hjälper maskiner att se (t.ex. ansiktsigenkänning) är vi klara nu (du behöver inte gå vidare till steg 3).

Steg 3: Komprimera det dynamiska intervallet för resultatet

När vi arbetar med ett utökat dynamiskt omfång sägs vi vara i "lightspace" (kvantimetrisk bildyta).

I slutet av steg 2 befinner vi oss i ljusrummet och vi måste återgå till bildytan.

Så det här steget 3 handlar om att komma tillbaka till bildutrymmet.

För att utföra steg 3, komprimera helt enkelt det dynamiska området för utgången från steg 2.

Om du känner till kamerans svarsfunktion, använd den helt enkelt för att få resultatet f (p (q)).

Om du inte känner till kamerans svarsfunktion är det bara att gissa.

Om du kvadrerade bildpixlarna i steg 1 är det nu dags att ta kvadratroten på varje bildpixel för att återgå till din gissning angående bildutrymme.

Steg 4: Du kanske vill prova några andra varianter

Deblurring är bara ett av många möjliga exempel. Tänk till exempel på att kombinera flera exponeringar.

Ta två bilder som de två jag har ovan. Den ena togs under dagen och den andra på natten.

Kombinera dem för att göra en skymningliknande bild.

Om du bara genomsnitt dem tillsammans ser det ut som skräp. Prova detta själv!

Men om du först utökar det dynamiska intervallet för varje bild, lägger till dem och sedan komprimerar summanas dynamiska område, ser det bra ut.

Jämför bildbehandling (lägg till bilderna) med kvantimetrisk bildbehandling (expanderar, lägger till och komprimerar sedan).

Du kan ladda ner min kod och mer exempelmaterial härifrån:

Steg 5: Gå vidare: Prova nu med HDR -bildkompositer

(Bilden ovan: HDR -svetshjälm använder kvantimetrisk bildbehandling för förstorade verklighetsöverlagringar. Se Slashgear 2012 12 september.)

Sammanfattningsvis:

ta en bild och använd följande steg:

1. utöka bildens dynamiska omfång;
2. bearbeta bilden;
3. komprimera resultatets dynamiska intervall.

Och om du vill ha ett ännu bättre resultat, prova följande:

fånga ett flertal olika exponerade bilder;

1. utöka det dynamiska området till ljusutrymme, enligt min tidigare Instruerbar på HDR;
2. bearbeta den resulterande kvantimetriska bilden, q, i ljusrum;
3. komprimera det dynamiska området genom tonkarta.

Ha kul och vänligen klicka på "Jag klarade det" och lägg upp dina resultat, så kommenterar jag gärna eller ger konstruktiv hjälp.