DIY laserstyrningsmodul för Arduino: 14 steg (med bilder)

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:46

I den här instruktionsboken kommer jag att demonstrera konstruktionen av en dubbelaxlig, en-spegel laserstråle styrmodul med hjälp av 3D-tryckta delar och billiga komponenter från eBay.

Detta projekt har likheter med Arduino Laser Show med Full XY Control och Arduino Laser Show With Real Galvos men jag tror är den första som använder en 3D -tryckt design med billiga solenoider. Jag lägger alla designfiler under GPLv3 så att designen kan förbättras och förbättras.

Även om jag för närvarande bara har monterat modulen och skrivit några mycket grundläggande testkoder, är min förhoppning att jag en dag kan ta den till nästa nivå genom att införliva vektorgrafikkoden från min tidigare instruerbara, super snabba analoga spänningar från Arduino.

Steg 1: Samla delar som inte är 3D-tryckta

Laserenheten består av följande delar:

• 4 mikro solenoider
• En 1/2 tum spegel
• Fyra M3 -skruvar

De speciella solenoider jag använde köptes på eBay för $ 1,45 styck. Den runda spegeln hittades i hantverksgången på HobbyLobby - ett paket med 25 kostade mig mindre än $ 3 dollar. Du kan också hitta speglar på eBay.

Du kommer också att behöva en billig laserpekare, igen, från eBay. En violett laser tillsammans med ett glödande vinylark är en utmärkt kombination för detta projekt!

En uppsättning hjälpande händer är inte nödvändigt, men kommer att vara mycket användbart för att hålla och placera laserpekaren. Ett stort bindemedelsklämma kan användas för att hålla strömbrytaren intryckt.

Du behöver en Arduino (jag använde en Arduino Nano) och ett sätt att driva solenoiderna. Som VajkF har uttalat i kommentarerna kan du använda färdiggjorda H-broar som de baserade på L298 eller L9110. Dessa är lätt tillgängliga på eBay för några dollar och kan också användas för att driva motorer och robotprojekt.

Eftersom jag inte hade en H-bro byggde jag min egen drivrutin av diskreta komponenter:

• Fyra bipolära NPN -transistorer (jag använde en MPS3704)
• Fyra motstånd (jag använde 1,2k ohm motstånd)
• Fyra dioder (jag använde en 1N4004)
• Ett 9V batteri och batterikontakt

De elektroniska komponenterna var från mitt labb, så jag har ingen exakt kostnad för dem, men om du inte redan har delarna eller kan ta bort dem är det förmodligen mer kostnadseffektivt att använda en förbyggd H-bro. Ändå kommer jag att tillhandahålla scheman för att bygga ditt eget.

Steg 2: 3D -utskrift av spegelstyrningsmodulen

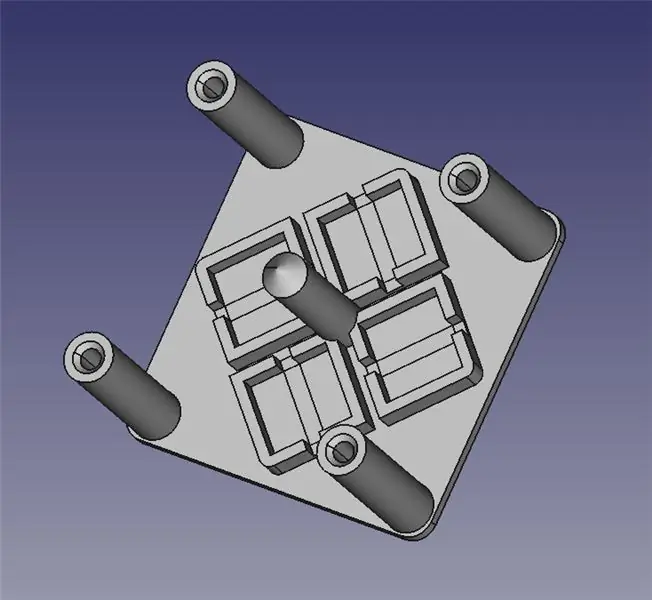
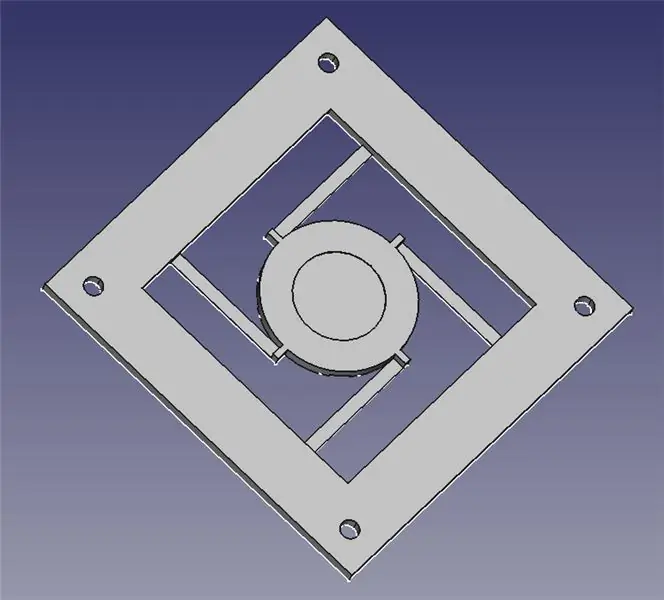
Laserstyrningsmodulen består av två 3D -tryckta delar: en bas för montering av fyra solenoider och en ledad plattform för spegeln.

Jag har bifogat de två STL -filerna för dig till 3D -utskrift, samt FreeCAD -filer om du behöver ändra designen. Allt innehåll är under GPLv3, så du är fri att göra och dela dina förbättringar!

Steg 3: Montera lasermodulen

• Använd varmt lim för att fästa de fyra solenoiderna på den nedre delen.
• Använd varmt lim för att fästa spegeln på mitten av den övre delen.
• Sätt in metallkolvarna i solenoiderna och placera sedan den övre delen på stolparna (men skruva inte ner den). Vrid toppstycket något och lyft varje kolv med en liten skruvmejsel. Skivans läpp ska glida in i spåret på kolven. Var försiktig, eftersom 3D -tryckta gångjärn är mycket ömtåliga. Med tålamod och eventuellt några misslyckade försök bör du kunna placera alla fyra kolvarna utan att vrida eller sätta press på gångjärnen.
• När alla kolvar är placerade sätter du i M3 -skruvarna delvis, men innan du drar åt dem trycker du försiktigt ner varje kolv och ser till att spegeln lutar fritt. Om den inte rör sig fritt eller hakar fast kan det vara nödvändigt att ta bort topplattan, bända av en eller flera solenoider och fästa den igen med en liten vinkel utåt (att placera distanser mellan den och den centrala stolpen kan hjälpa till med detta).

Steg 4: Skriv ut laserpekarkragen

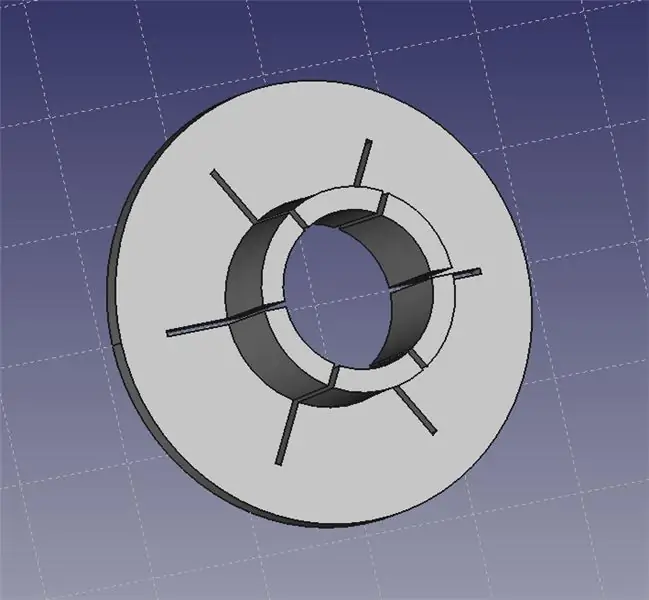
Laserpekarkragen passar på laserpekarens huvud. Du kan sedan använda en uppsättning hjälpande händer för att ta tag i kragen och låta dig placera lasern exakt på din bänk.

Steg 5: Montera körkretsen

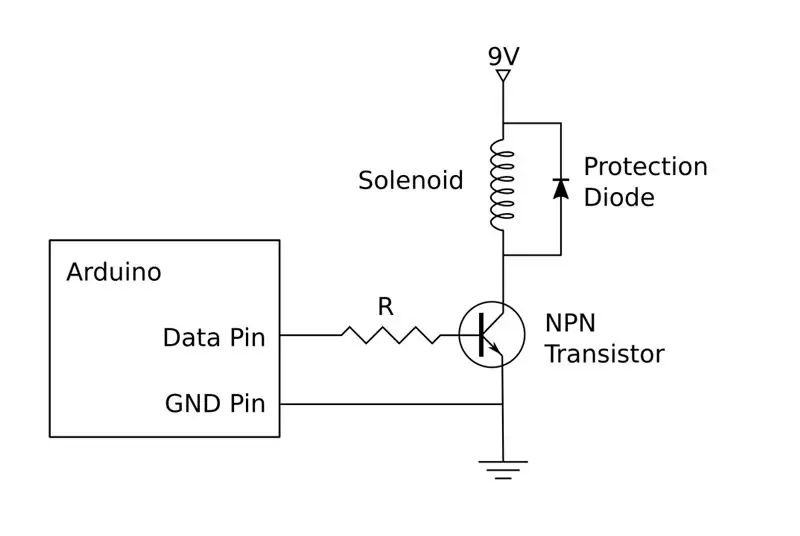
Drivkretsen visas i schemat. Som tidigare nämnts är min version byggd av diskreta komponenter, men du kan också använda en lättillgänglig H-bro. Om du väljer att bygga din egen måste du bygga fyra kopior av denna krets, en för var och en av de fyra solenoiderna.

Varje krets kommer att ansluta till en Arduino -stift, två för styrning av vänster och höger magnetventil, och två för upp och ner magnetventiler. Dessa måste anslutas till PWM -kompatibla stift, så här:

• Pin 9: Up Solenoid
• Pin 3: Down Solenoid
• Pin 11: Vänster magnetventil
• Stift 10: Höger magnetventil

Ett enda 9V -batteri kan användas för att driva alla fyra solenoiddrivkretsar eller så kan du använda en strömförsörjning vid en bänk. Arduino kommer att driva från USB -ström och bör inte anslutas till den positiva sidan av 9V -batteriet. Den negativa sidan av batteriet används dock som markreferens och bör anslutas till GND-stiftet på Arduino såväl som till sändarpinnarna på transistorerna.

Steg 6: Ladda upp provkoden

Exempelkoden har uppdaterats med följande funktioner:

• Justerar PWM -frekvensen så att mekanismen är nästan tyst vid låga hastigheter. Surret i Motion Test 1 är helt borta!
• Lägger till som spänningsekvationer baserade på papperet av Schimpf för att "linearisera" det icke-linjära svaret från solenoiderna.

Jag har också inkluderat en implementering av en Lorenz Attractor baserad på koden från den här bloggen.

Resultatens trohet lämnar ganska mycket att önska, men jag arbetar fortfarande med det!:)

De efterföljande stegen illustrerar några av de tekniker som används i koden.

Steg 7: Sänka volymen

I mitt rörelsestest 1 kan du höra ett högt surr, särskilt under upp och ner rörelse. Det visar sig att detta orsakades av att standard PWM -hackfrekvensen för Arduino var inom det hörbara området. Den snabba omkopplingen av spolens spänning till och från skulle få dem att vibrera vid den frekvensen, vilket gör dem till små små högtalare.

För att lösa detta problem ökade jag PWM -frekvensen i koden:

#define PWM_FREQ_31372Hz 0x01 // Ställer in PWM -frekvensen till 31372,55 Hz #definiera PWM_FREQ_3921Hz 0x02 // Ställer in PWM -frekvensen till 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Ställer in PWM -frekvens (TCR1_TQ1_TQ1_TQ1_TQ1_TQ1_TQT_QTQTQQT) & 0b11111000) | frekvens; // Ställ in timer1 (stift 9 & 10) frekvens TCCR2B = (TCCR2B & 0b11111000) | frekvens; // Ställ in timer2 (stift 3 och 11) frekvens}

Att ställa in Arduino PWM -frekvensen är ett användbart trick för att tysta ner solenoider eller motorer. Experimentera med de olika valen av frekvenser för att se vilken som ger dig de bästa resultaten. Även om det innebär lite mer avancerad programmering, är en bra resurs om hur timern fungerar här.

Steg 8: Stämma spänningarna för att minska distorsion

Mina första rörelsestester visade att det var signifikant snedvridning av solenoidernas svar. I Motion Test 3 (vänster figur) blev det som skulle vara en cirkulär spiral istället en rektangulär bana med ojämna kanter.

Att lösa detta problem krävde lite matematik, men jag kunde hitta ett fantastiskt papper på webben som hjälpte mig att förstå problemet tillräckligt bra för att lösa det i programvara.

Det som följer följer dig genom processen jag gick igenom för att justera systemet och förbättra utseendet på de resulterande spåren!

Steg 9: Perfekt programvara, med matematik

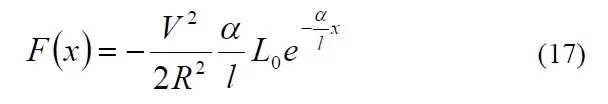
Hemligheten med att justera systemet visade sig vara ett utmärkt papper som heter "A Detailed Explanation of Solenoid Force" av Paul H. Schimpf vid Eastern Washington University (länk). I synnerhet gav ekvation 17 mig solenoidkraften i termer av olika termer.

Följande termer var lätta att mäta:

• R - Motståndet hos min solenoid
• l - Solenoidens längd
• x - Kolvens förskjutning i solenoiden
• V - Spänningen över solenoiden

Jag visste också att kraften som släpptes ut av solenoiden måste balansera kraften från de 3D-tryckta fjädrarna på spegeln med två axlar. Kraften hos en fjäder styrs av Hookes lag, som sägs enligt följande:

F = -kx

Även om jag inte visste värdet av k, visste jag åtminstone att kraften jag fick ur ekvation 17 från Schimpfs papper måste motsvara kraften från Hookes lag.

Värdet på alfa (α) var svårt. Även om ekvationerna 13 och 14 visade hur man beräknade dessa värden från solenoidens (A) område, antalet varv (N) och magnetiska permeabilitetsvärden (μ), ville jag inte behöva riva isär en solenoid för att räkna antal varv, och jag visste inte heller materialet ur vilket min solenoidkärna gjordes.

Steg 10: En billig komponenttestare sparar dagen

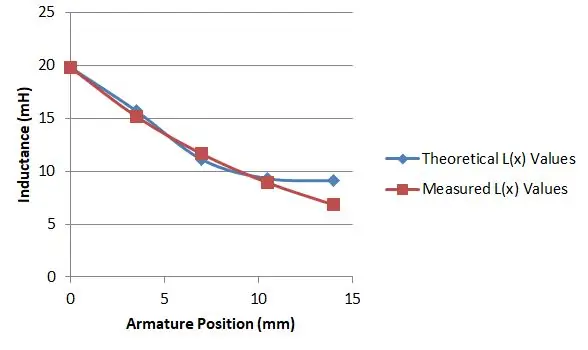
Det visade sig dock att ekvation 15 och 16 gav mig det jag behövde. Jag hade en billig M328 komponenttestare som jag hade köpt från eBay för $ 10. Den kunde använda den för att mäta induktansen hos min solenoid och jag fann att genom att trycka in ankaret på olika djup gav det mig olika induktionsvärden.

Att mäta det med ankaret helt insatt gav mig värdet L (0).

Längden på min solenoid var 14 mm, så jag mätte induktansen med ankaret i fem lägen och detta gav mig olika värden för L (x):

• L (0,0) = 19,8 mH
• L (3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L (14) = 9,1 mH

Jag använde sedan ett kalkylblad för att plotta mina värden kontra värdet på ekvation 15 och 16, för ett visst val av μr och varierade sedan mitt val tills jag hittade en bra matchning. Detta hände när μr var 2,9, som visas i grafen.

Steg 11: Hitta fjäderkonstanten K, lösa problemet

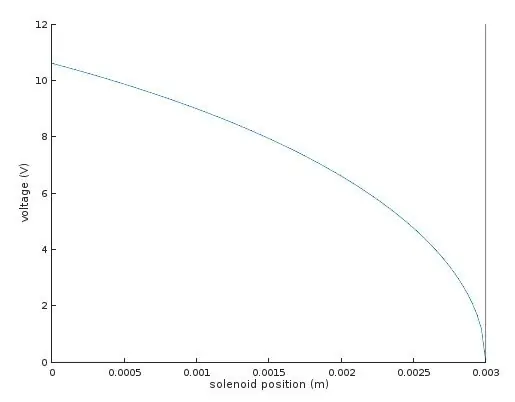
Det enda kvarvarande okända var K, vårkonstanten. Jag mätte detta genom att applicera 9V på en av solenoiderna i min dubbelaxliga enhet och mäta avståndet där spegeln drogs ner. Med dessa värden kunde jag lösa ekvationerna för K, som jag fann var runt 10.41.

Jag hade nu de värden jag behövde för att beräkna dragningen av solenoiden vid olika positioner längs slaget. Genom att ställa in F (x) lika med fjäderkraften från Hookes lag kan jag lösa den erforderliga spänningen V.

Diagrammet visar den spänning som krävs för att flytta solenoiden till önskat läge x.

Till höger, där spänningen är noll och positionen är 3 mm, motsvarar detta magnetens neutrala vilopunkt när de 3D -tryckta gångjärnen är helt avslappnade. Att flytta vänster på grafen motsvarar att man drar ankaret in i solenoiden mot dragningen av de 3D-tryckta gångjärnen-detta kräver initialt mer spänning, men när ankaret blir djupare i solenoiden ökar dragningen och den nödvändiga drivspänningen avsmalnar.

Detta förhållande är definitivt olinjärt, men med ekvationerna från Schimpfs papper kan jag skriva min Arduino-kod för att mata ut rätt spänningar så att strålavböjningen är linjär:

float positionToVoltage (float x) {

// Återställa kraft som utövas av gångjärn (Hookes lag) vid önskat x. const float spring_F = -spring_K * (x - spring_X0); // Spänning så att dragkraften för solenoiden matchar // återställande kraft för gångjärnen retur kvrt (-2*R*R*(-fjäder_F)*solenoid_len/(en*L_0*exp (-a*x/solenoid_len)))); }

Detta leder till en mycket mer cirkulär spiral än i mitt ursprungliga rörelsestest. Uppdrag slutfört!

Steg 12: Frågor och svar om förarkretsen med diskreta komponenter

Varför kan jag inte ansluta solenoiden direkt till Arduino?

Det är en fråga om hur mycket ström Arduino kan ge utan att skada den. Detta är cirka 40mA per stift. Genom att veta att Arduino fungerar vid 5V, kan vi använda Ohms lag för att beräkna det lägsta minimimotståndet för lasten (i detta fall solenoiden). Att dividera 5 volt med 0,040 ampere ger oss, 125 ohm. Om lasten har ett större motstånd kan vi ansluta den direkt till Arduino, annars kan vi inte. En liten solenoid har vanligtvis ett motstånd på 50 ohm, så vi kan inte köra den direkt från Arduino. Om vi gjorde det skulle det dra 100mA, vilket är klart för mycket.

Varför använder du 9V för solenoiden, men 5V för Arduino?

Arduino går på 5V, men det här är lite för lite för en solenoid. Med hjälp av en transistor kan vi välja en spänning för solenoiden som är oberoende av 5V som används för Arduino.

Hur vet jag om en transistor är lämplig för detta projekt?

Precis som Arduino är det stora kravet att strömmen som flyter genom solenoiden inte överstiger de maximala värdena för transistorn (i synnerhet kollektorströmmen). Vi kan enkelt beräkna det värsta scenariot genom att mäta solenoidens motstånd och sedan dividera matningsspänningen med det. När det gäller en 9V matningsström för solenoiderna och ett solenoidmotstånd på 50 ohm, sätter det värsta fallet oss på 180mA. MPS3704 är till exempel klassad för en maximal kollektorström på 600 mA, vilket ger oss en marginal på cirka 3.

Hur bestämmer jag minimivärdet av motståndet mellan Arduino -utgången och basen på transistorn?

Utgången från Arduino kommer att ansluta basbenet på de bipolära transistorerna genom ett strömbegränsande motstånd. Eftersom Arduino fungerar vid 5V kan vi återigen använda Ohms lag för att beräkna det motstånd som krävs för att begränsa strömmen under 40mA. Det vill säga dela 5 volt med 0,04 ampere för att få ett värde på minst 125 ohm. Högre motståndsvärden minskar strömmen, vilket ger oss en ännu större säkerhetsmarginal.

Finns det ett maximivärde för det motståndet som jag inte bör överskrida?

Det visar sig, ja. En transistor har en så kallad strömförstärkning. Till exempel, om förstärkningen är 100, betyder det att om vi sätter 1mA i basen, kommer upp till 100mA att flöda genom belastningen som transistorn styr. Om vi sätter 1,8mA i basen, kommer upp till 180mA att flöda genom lasten. Eftersom vi tidigare beräknat att vid 9V rinner 180mA genom solenoiden, då är en basström på 1,8mA "sweet spot", och mindre och vår solenoid kommer inte att slås på helt.

Vi vet att Arduino släpper ut 5V och vi vill att 1,8mA ström ska flöda, så vi använder Ohms lag (R = V/I) för att beräkna motståndet (R = V/I). 5V dividerat med 1,8mA ger ett motstånd på 2777 ohm. Så med tanke på de antaganden vi gjorde förväntar vi oss att motståndet måste ligga mellan 125 och 2777 - att välja något som 1000 ohm ger oss en ganska bra säkerhetsmarginal åt båda hållen.

Steg 13: Analys av aktuella problem och möjliga lösningar

Den nuvarande prototypen visar potential, men flera problem kvarstår:

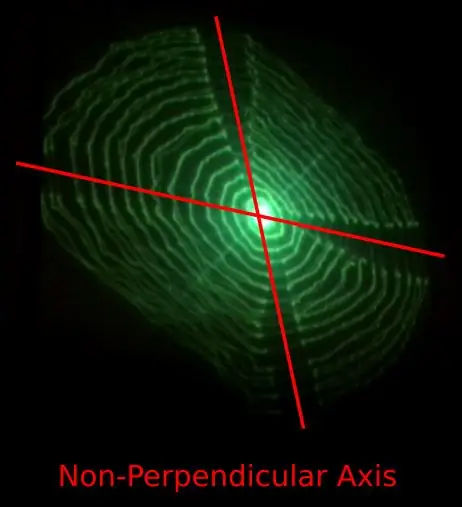
1. Rörelse längs X- och Y -axeln verkar inte vara vinkelrät.
2. Det blir ett hopp när spegeln ändrar riktning.
3. Upplösningen är ganska låg och det finns synliga trappstegsmönster.
4. Vid högre rörelsehastigheter förvrängs laserns väg av vibrationer och ringningar.

Problem 1) kan orsakas av utformningen av de 3D -tryckta flexibla gångjärnen som överför rörelse längs en axel till den vinkelräta axeln.

Utgåva 2) beror på att kopplingen mellan drivkolvarna och spegelplattformen släpps, detta får spegeln att rycka och hoppa över vid övergångar mellan X- och Y -axeln. Denna plötsliga rörelse leder till en mörkare X -formad lucka där laserpunkten gör ett snabbare okontrollerat drag.

Problem 3) uppstår eftersom standard Arduino PWM bara har 255 nivåer och en hel del av dem går till spillo på grund av spänningskurvans form. Detta kan förbättras avsevärt genom användning av timer1, som är 16-bitars och skulle kunna ha 65536 unika värden.

Problem 4) uppstår eftersom spegeln och solenoidens glidarmatur (kolvar) utgör en betydande mängd rörlig massa.

Eftersom problem 1) och 2) är relaterade till den mekaniska konstruktionen kan en möjlighet vara att ta bort metallkolvarna och ersätta dem med små sällsynta jordartsmagneter som fästs direkt på lutningsplattan. Magnetventilerna skulle vara en öppen spole som skulle attrahera eller avvisa magneterna utan att få fysisk kontakt. Detta skulle leda till mjukare rörelse och eliminera risken för ryck, samtidigt som den totala massan minskar.

Minskning av massa är den primära lösningen för problem 4), men eventuella återstående problem kan riktas direkt i programvara genom att implementera en rörelsekontrollprofil i programvara för att accelerera och sakta ner spegeln på ett kontrollerat sätt. Detta görs redan i stor utsträckning i firmware för 3D -skrivare och liknande metoder kan också fungera här. Här är några resurser relaterade till rörelsekontroll som gäller 3D -skrivare:

• "Mathematics of Motion Control Profiles", Chuck Lewin (länk)
• "Jerk Controlled Motion Explained", (länk)

Jag misstänker att tillägg av en trapetsformad rörelsekontrollprofil skulle tillåta att spegeln körs med mycket högre hastigheter utan ringning eller vibrationsartefakter.

Steg 14: Framtidsarbete och möjliga tillämpningar

Även om utvecklingen av lösningar på dessa problem kommer att kräva mycket arbete, hoppas jag att denna öppen källkodsmodul kan bli ett prisvärt alternativ till galvanometerbaserade projekt i sådana applikationer som:

• En billig lasershow för DJ och VJ.
• En elektromekanisk vektordisplay för ett vintage arkadspel som Vectrex.
• En DIY SLA 3D-skrivare av harts som i andan av RepRap-rörelsen kan skriva ut sin egen laserstyrningsmodul.
• Digital panorering eller optisk bildstabilisering för kameror.

Andra priset i Arduino -tävlingen 2017