Mät temperatur från PT100 med Arduino: 6 steg (med bilder)

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-31 10:25

PT100 är en motståndstemperaturdetektor (RTD) som ändrar dess motstånd beroende på dess omgivande temperatur, den används i stor utsträckning för industriella processer med långsam dynamik och relativt breda temperaturområden. Den används för långsamma dynamiska processer eftersom RTD har långsamma responstider (som jag pratar mer om senare) men är korrekta och har låg drift över tiden. Vad jag ska visa dig i denna instruerbara skulle inte vara upp till industriell standard, men det kommer att utsätta dig för ett alternativt sätt att mäta temperatur än att använda LM35 som många hobbyister skulle känna till och kretsteorin visas kan appliceras på andra sensorer.

Steg 1: Komponenter

1x PT100 (två trådar)

1x Arduino (valfri modell)

3x 741 driftförstärkare (LM741 eller UA741)

1x 80ohm motstånd

2x 3,9 kohm motstånd

2x 3,3 kohm resistorer

2x 8,2 kOhm motstånd

2x 47kohms motstånd

1x 5kohms potentiometer

1x två terminaler eller 8x 1,5V AA -batterier

Jag använder en PT100 med två trådar, tre och fyra ledare PT100 kommer att ha olika kretsar. Motståndsvärdena för de flesta av dessa behöver inte vara exakt samma som ovan men om det finns ett par motstånd, dvs 3.9Kohms, om du bytte dem mot låt oss säga 5k, måste du byta båda för 5k som då måste vara densamma. När vi får kretsen säger jag effekten av att välja olika värden. För operationsförstärkare (op -förstärkare) kan du använda andra op -förstärkare men det är de jag använde.

Steg 2: Wheatstone Bridge

Jag måste först prata om formeln för att få temperaturen från motståndet för PT100 innan jag pratar om den första delen av kretsen, formeln för motståndet är följande:

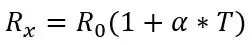
där Rx är PT100 -resistansen, R0 är PT100 -resistansen vid 0 grader C, α är temperaturmotståndskoefficienten och T är temperaturen.

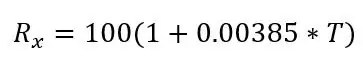
R0 är 100ohms eftersom detta är en PT100, om det var en PT1000 skulle R0 vara 1000ohms. α är 0,00385 ohm/grader C taget från databladet. Det finns också en mer exakt formel som kan hittas här men ovanstående formel kommer att göra för detta projekt. Om vi införlivar formeln kan vi beräkna temperaturen för ett givet motstånd:

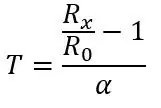
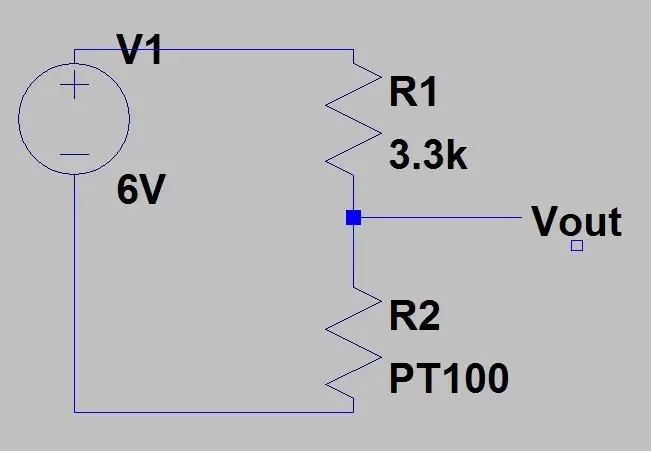
Låt oss säga att vi vill mäta något som skulle ha ett temperaturintervall på -51,85 till 130 grader C och vi placerade PT100 i kretsen som visas i bild 1. Använd ekvationen ovan och ekvationen för spänningen från en spänningsdelare (visas i den första bilden) kan vi beräkna spänningsområdet. Botten av intervallet T = -51,85 (80ohms)

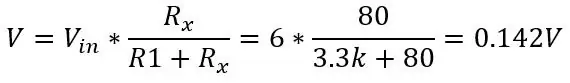
och vid 130 grader (150 ohm):

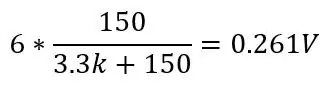
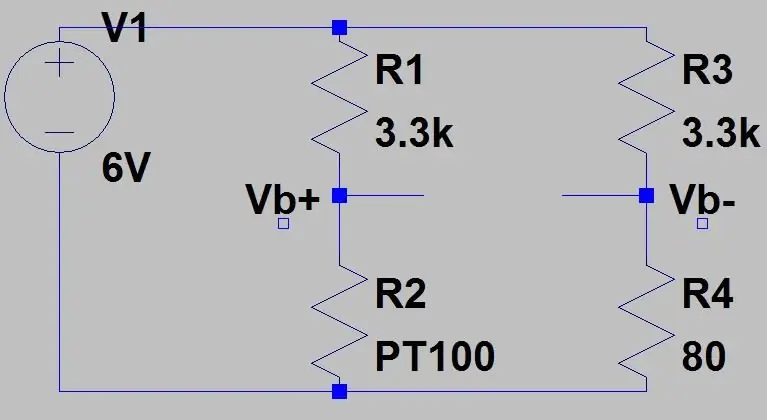
Detta skulle ge ett intervall på 0.1187V och en DC -förskjutning på 0.142 eftersom vi vet att vår temperatur aldrig kommer att komma under -51.85 grader C, detta kommer att minska känsligheten i det område vi bryr oss om (80 till 130ohms) när vi förstärker denna spänning. För att bli av med denna DC -förskjutning och öka vår känslighet kan vi använda en Wheatstone -bro som visas på den andra bilden.

Utgången från den andra spänningsdelaren (Vb-) kommer att subtraheras från den första spänningsdelarens utgång (Vb+) med en differentialförstärkare senare. Formeln för utgången från bron är bara två spänningsdelare:

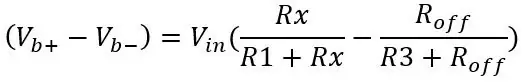
Spänningen ut för PT100 är 80 ohm och använder de andra värdena på bilden:

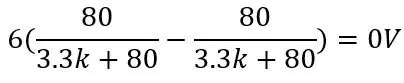
och för Pt100 som är 150 ohm:

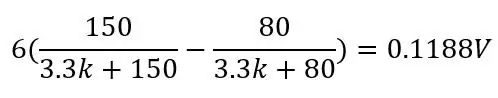
Genom att använda Wheatstone blir vi av med DC -förskjutningen och ökar känsligheten efter förstärkning. Nu när vi vet hur Wheatstone -bron fungerar kan vi prata om varför vi använder 80ohms och 3.3kohms. 80ohms förklaras på något sätt utifrån formeln ovan, välj det här värdet (vi kallar detta offsetmotståndet Roff) för att vara det lägsta intervallet för din temperatur eller ännu bättre, något under botten av ditt intervall, om detta används för ett styrsystem för temperaturreglering eller något liknande, skulle du vilja veta hur låg temperaturen kommer under ditt temperaturintervall. Så om -51,85C är botten av ditt intervall, använd 74,975 ohm (-65 grader C) för ditt Roff.

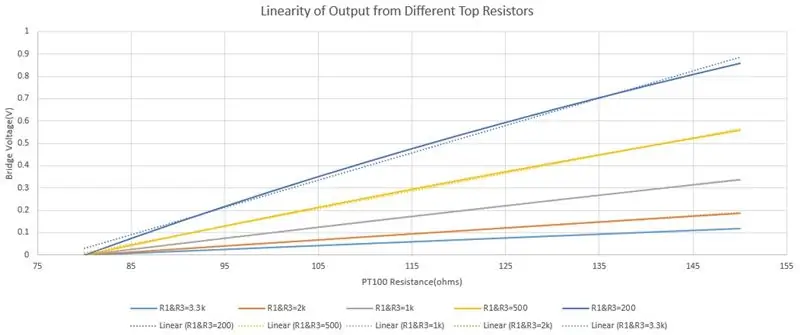
Jag valde 3.3k för R1 och R3 av två skäl, för att begränsa strömmen och öka utmatningens linearitet. Eftersom PT100 ändrar motstånd på grund av temperatur, ger för mycket ström genom det felaktiga avläsningar på grund av självuppvärmning så jag valde en maxström på 5-10mA. När PT100 är 80ohms är strömmen 1,775mA så säkert under maxintervallet. Du minskar motståndet för att öka känsligheten, men detta kan ha en negativ effekt på linjäriteten, eftersom vi kommer att använda ekvationen för en linje senare (y = mx+c) som har en olinjär utmatning kommer att introducera fel. Den tredje bilden har en graf över bryggutgången med olika toppmotstånd, den heldragna linjen är den faktiska utsignalen och den streckade linjen är den linjära approximationen. Du kan se i den mörkblå grafen (R1 & R3 = 200ohms) ger det största spänningsområdet men utgången är minst linjär. Den ljusblå (R1 & R3 = 3,3 kohms) ger det minsta spänningsområdet men den streckade linjen och den heldragna linjen överlappar varandra och visar att dess linearitet är mycket bra.

Ändra gärna dessa värden för att passa din applikation, även om du ändrar spänningen, se till att strömmen inte blir för hög.

Steg 3: Förstärkning

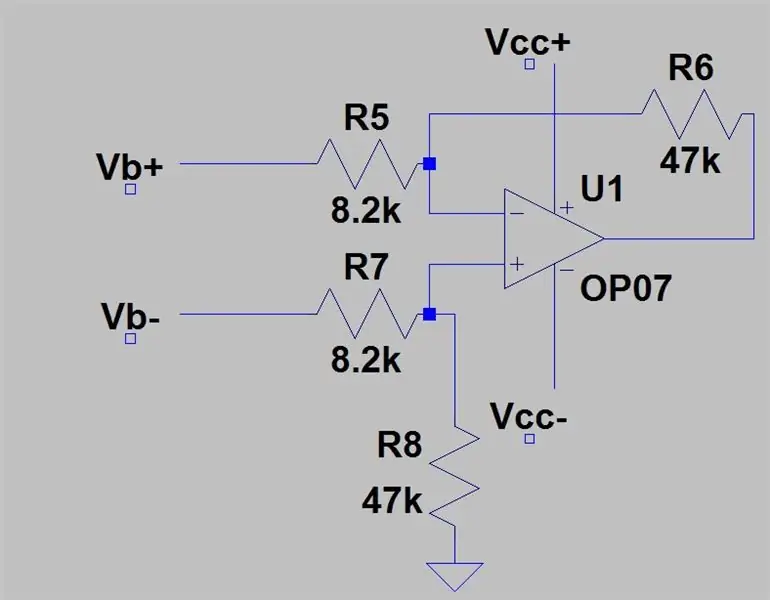
I det sista steget fann vi att utgångsområdet för de två spänningsdelarna som subtraherades var 0 till 0.1187 men vi har inte pratat om hur man subtraherar dessa spänningar. För att göra detta behöver vi en differentialförstärkare som kommer att subtrahera en ingång från den andra och förstärka detta med förstärkarens förstärkning. Kretsen för en differentialförstärkare visas på den första bilden. Du matar in Vb+ i inverteringsingången och Vb- i den icke-inverterande ingången och utgången är Vb+- Vb- med en förstärkning på en dvs ingen förstärkning men genom att lägga till motstånden som visas på bilden lägger vi till en förstärkning på 5,731. Vinsten ges av:

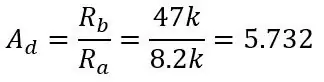
Ra är R5 & R7 och Rb är R6 & R8, spänningen ut ges av:

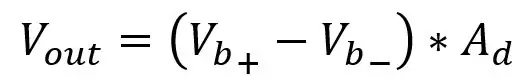
Det finns två problem med att bara ansluta denna förstärkare till bryggans utgång, laddningseffekten och ändra förstärkningen. För att ändra förstärkarens förstärkning krävs att du byter minst två motstånd eftersom de två motståndsparen måste vara desamma, så att ha två krukor som måste ha samma värde skulle vara irriterande så vi kommer att använda något som kallas en instrumentförstärkare som jag pratar om nedan. Belastningseffekten är ingångsmotstånden i förstärkaren som påverkar spänningsfallet över PT100, vi vill att spänningen över PT100 ska vara oförändrad och för att göra detta kan vi välja mycket stora motstånd för ingångsmotstånden så att parallellmotståndet för PT100 och ingångsmotståndet är mycket nära PT100 -motståndet men detta kan orsaka problem med brus och spänningsutmatning som jag inte kommer att gå in på. Välj bara mittintervall i Kohms -intervallet, men som jag sa, att ha små motstånd är också dåligt så vi kommer att ändra kretsen lite.

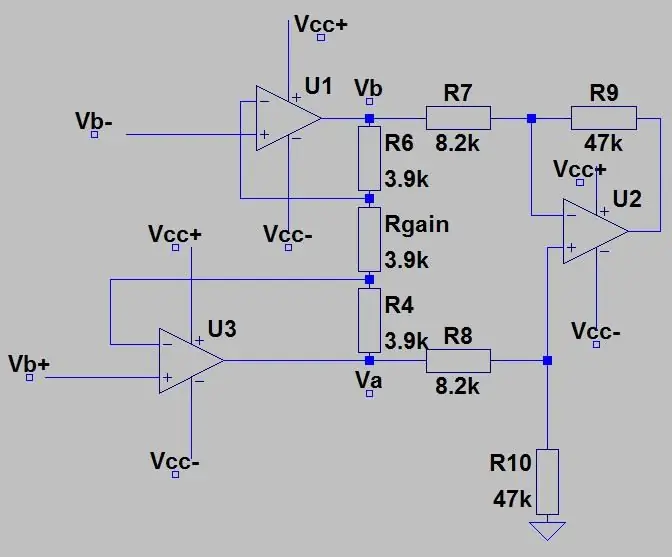
I den andra bilden har vi utgången från bron ansluten till en instrumentförstärkare som fungerar som en buffertförstärkare för att separera de två halvorna av kretsarna (bryggan och förstärkningen) och gör det möjligt att förstärka ingången genom att bara ändra en potentiometer (Rgain). Förstärkningen av instrumentförstärkaren ges av:

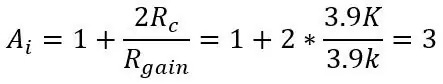
där Rc är de två 3,9k motståndet ovanför och under potten.

Genom att minska Rgain ökar amplifieringen. Sedan vid punkt Va och Vb (förstärkt Vb+ och Vb-) är det bara en differentialförstärkare som tidigare och kretsens totala förstärkning är bara vinsterna multiplicerade tillsammans.

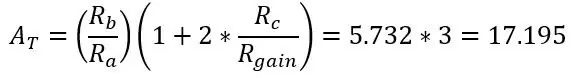
För att välja din vinst vill du göra något som vi gjorde tidigare med Roff, vi bör välja ett motstånd strax över din max temperatur i ditt intervall bara om det går över. Eftersom vi använder Arduino som har en 5V adc, bör kretsens maximala uteffekt 5V vid den högsta temperatur du valt. Låt oss välja 150ohms som maxmotståndet och bryggspänningen som inte är förstärkt var 0.1187V, förstärkningen vi behöver är 42.185 (5/0.1187)

Låt oss säga att vi behåller Ra, Rb och Rc som 8,2k, 47k och 3,9k, vi behöver bara hitta värdet för potten Rgain:

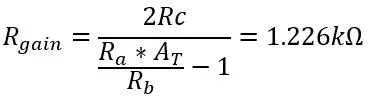
Så för att få hela 5 volt ur det temperaturintervall vi använder, ändra värdet på Rgain till 1,226k. Utgångsspänningen som kommer ut från differentialförstärkaren ges av:

Steg 4: Strömförsörjning av kretsen

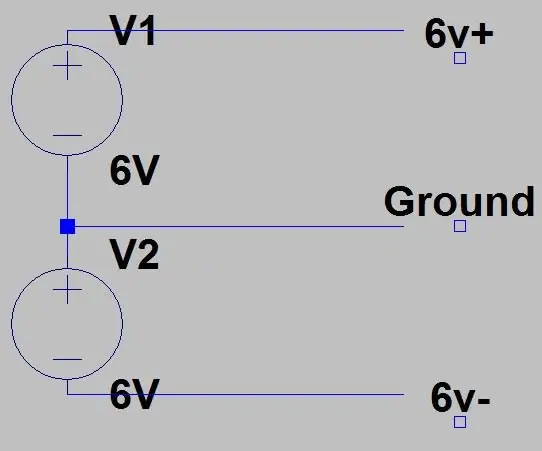
Detta är det sista steget i kretsen, du kanske har lagt märke till Vcc+ och Vcc- på op-amp-kretsarna, detta beror på att de behöver både positiv och negativ spänning för att fungera korrekt, du kan få enstaka op-ampere men jag bestämde mig att använda den här förstärkaren eftersom det var vad jag hade. Så vi levererar +6V och -6V, det finns tre sätt vi kan göra detta. Den första visas i den första bilden där vi måste två strömförsörjningar eller två utgångsterminaler från en enda strömförsörjning, har båda vid 6V och har en positiv utgång ansluten till den andra av den andra. 6V för toppförsörjningen kommer att vara vår +6V, bottenförsörjningens positiva är GND och minus för bottenförsörjningen är -6V. ANSLUT ENDAST SOM HÄR OM GND -värdena för de två leveranserna är separerade ELLER DET SKADAR DIN STRÖMFÖRSÖRJNING. Alla kommersiella strömförsörjningar skulle ha separerat GND, men om du vill kontrollera, använd kontinuitetstestaren på din multimeter, om det surrar, använd inte den här inställningen och använd nästa. På min hemmagjorda matning sprängde jag säkringen när jag gjorde detta.

På den andra bilden är den andra installationen vi kan ha, det kräver en matning för att ha dubbel spänning från den andra men skadar inte matningen om GND: erna är anslutna. Vi har två tillbehör, en vid 12V och en annan vid 6V. 12V kommer att fungera som vår +6V, 6V av den andra leveransen kommer att fungera som GND och de två faktiska GND: erna från leveranserna kommer att fungera som -6V.

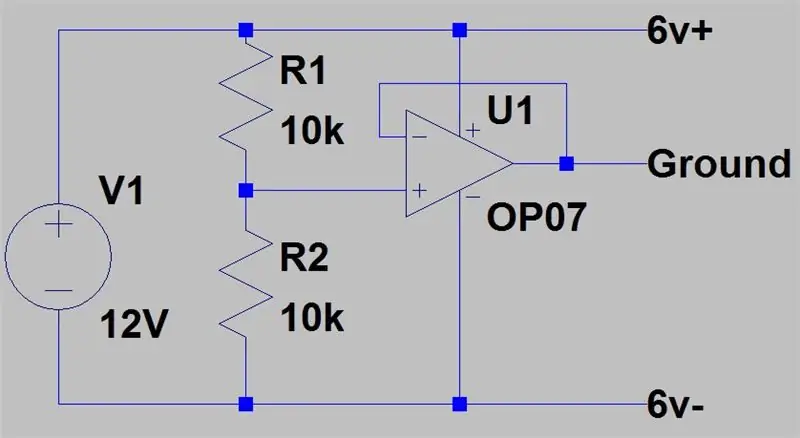
Denna sista inställning är för nätaggregaten med endast en utgång, den använder en buffertförstärkare med förstärkning 1 för att skapa en virtuell mark genom att passera halva matningsspänningen genom buffertförstärkaren. Då fungerar 12V som +6V och den faktiska GND -terminalen är -6V.

Om du vill använda batterier föreslår jag den första installationen, men ett problem med batterier är att spänningen sjunker när de börjar dö och spänningen från bron kommer att sjunka också, vilket ger fel temperaturavläsningar. Du kan naturligtvis läsa spänningen från batterierna och inkludera dem i beräkningarna eller använda regulatorer och fler batterier. I slutändan är det upp till dig.

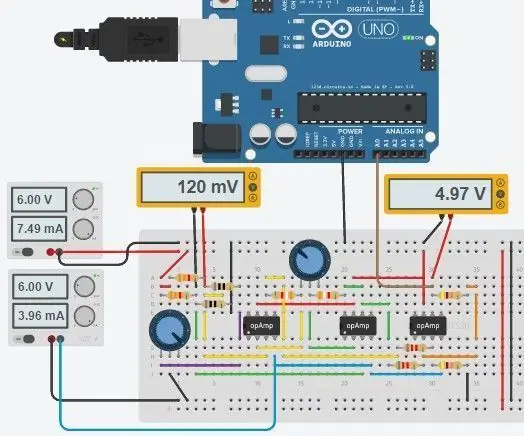
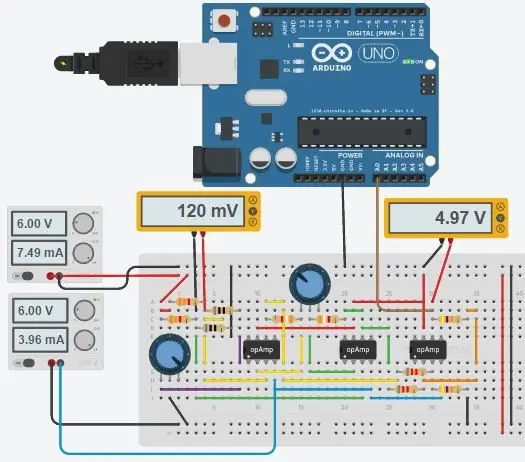
Steg 5: Full krets och kod

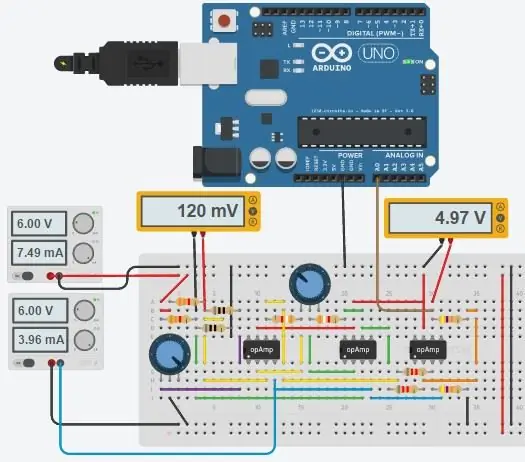
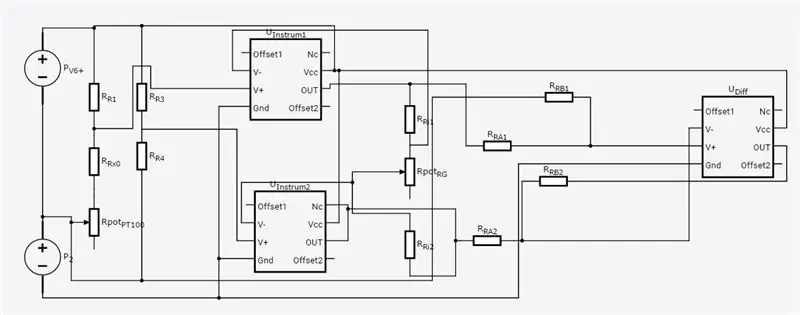
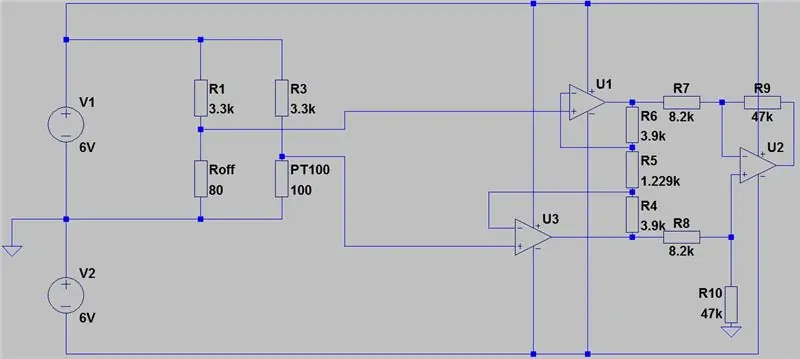
Hela kretsen visas ovan och den gjordes i Autodesks nya Circuits.io som låter dig skapa kretsar på brödbräda, redigera kretsschema (visas i bild 2) och PCB -diagram och den bästa delen, låter dig simulera kretsen från brödbrädet och kan till och med programmera en Arduino och ansluta den i breadboard -läget, längre ner på sidan är simuleringen och du kan leka med två grytor. Om du vill kopiera kretsen och sätta in dina egna värden kan du hitta kretsen här. Den första potten är 70ohms och i serie med ett 80ohm motstånd som simulerar PT100 med ett intervall på 80-150ohms, den andra potten är förstärkningen från instrumentförstärkaren. Tyvärr använde jag ett bibliotek som jag laddade ner för min kod, så Arduino ingår inte i kretsen nedan men det finns bara två extra ledningar du behöver ansluta. Om du är mer bekväm med LTspice inkluderade jag en asc -fil med kretsen.

Anslut A0 -stiftet till utgången på differentialförstärkaren

Anslut Arduino GND till kretsens GND (INTE -6V)

Och det är kretsen klar, nu till koden. Tidigare nämnde jag att vi kommer att använda formeln y = mx+c, nu ska vi beräkna m (lutningen) och c (förskjutningen). I Arduino läser vi spänning men temperaturekvationen behöver oss att känna till PT100: s motstånd så ett sätt vi kan göra detta är genom att ersätta Serial.println (temp) med Serial.println (V) och spela in spänning och motstånd vid två temperaturer. När du gör detta test, lämna PT100 ensam en stund, ungefär en minut eller två och håll dig borta från värmekällor (solljus, bärbar fläkt, din kropp, etc.).

Den första punkten vi kan ta är rumstemperatur, när du har kretsen ansluten och fungerar, registrera spänningen (Vt1) avläst av Arduino på den seriella bildskärmen och koppla snabbt bort PT100 och registrera dess motstånd (Rt1), lägg inte din händerna på sonden vid urkoppling eftersom detta kommer att ändra motståndet. För den andra temperaturen kan vi placera sonden i isvatten eller varmt vatten (var försiktig om du använder varmt vatten) och upprepa vad vi gjorde innan vi hittade Vt2 och Rt2. Strax efter att du placerat sonden i vätskan väntar du en minut eller två på att motståndet löser sig. Om du är intresserad av tidssvaret för PT100, registrera spänningen från den seriella bildskärmen varannan sekund eller så och vi kan rita en graf från detta och jag ska förklara det senare. Med hjälp av de två spänningarna och motstånden kan vi beräkna lutningen enligt följande:

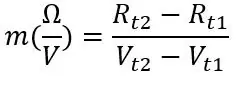
Rt1 och Rt2 är motstånden vid de två temperaturerna och samma gäller för spänningarna Vt1 och Vt2. Från lutningen och en av de två uppsättningar punkter du registrerade kan vi beräkna förskjutningen:

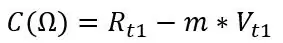
C ska vara nära din riktiga Roff, Från min simulering beräknade jag dessa värden:

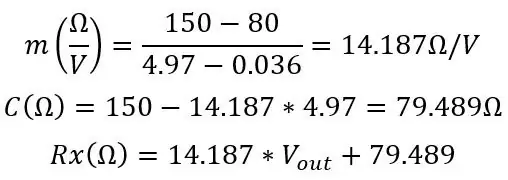
Från detta motstånd kan vi hitta vår temperatur med hjälp av formeln vi hade i början:

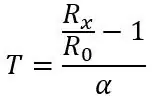
Och det är det, koden för Arduino finns nedan. Om du har några problem är det bara att lämna en kommentar så ska jag försöka hjälpa till.

Det finns inga bilder på kretsen jag gjorde som jag gjorde den för ett tag sedan och har inte PT100 längre att göra om och testa men du får bara tro mig att den fungerar. Det finns inte mycket om PT100 på Instructables som jag hittade så det var därför jag gjorde denna ible.

I nästa steg kommer jag att prata om tidssvaret för PT100 och om du inte är intresserad av matte, när du mäter en temperaturförändring, låt PT100 nöja sig i någon minut innan du läser.

Om du är intresserad av att se andra projekt jag gjort, besök min

Blogg: Roboroblog

YouTube -kanal: Roboro

Eller titta på mina andra instruktioner: här

Om HTML -filen stör med koden nedan bifogas koden

* Denna kod beräknar temperaturen med en PT100

* Skrivet av Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- Från-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

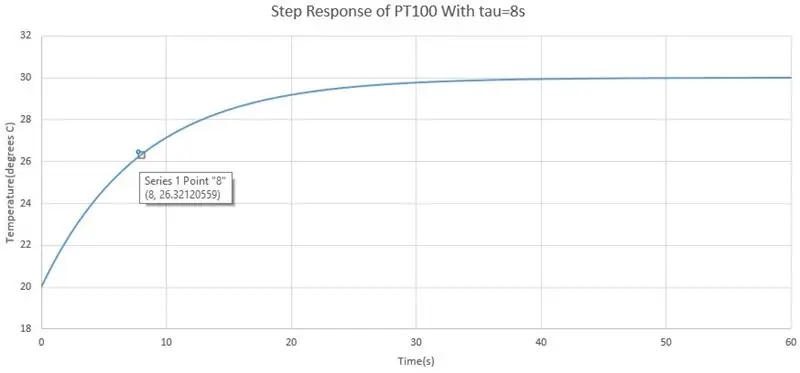
Så jag nämnde att PT100 har ett långsamt svar men vi kan få en formel för den aktuella temperaturen som läses av PT100 när som helst t. Svaret från PT100 är ett första ordningssvar som kan skrivas med Laplace -termer, dvs. överföringsfunktion, som:

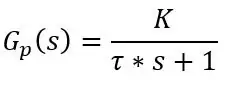
där tau (τ) är tidskonstanten, K är systemets förstärkning och s är Laplace -operatören som kan skrivas som jω där ω är frekvens.

Tidskonstanten berättar hur lång tid det tar för ett första ordningssystem att sätta sig vid sitt nya värde och en regel eller tumme är att 5*tau är hur lång tid det tar att slå sig ned i det nya steady state. Förstärkningen K berättar hur mycket ingången kommer att förstärkas. Med PT100 är förstärkningen hur mycket motståndet förändras dividerat med temperaturförändringen, från att välja två slumpmässiga värden från detta datablad fick jag en förstärkning på 0,3856 ohm/C.

Innan jag sa att du kunde registrera spänningen varannan sekund efter att du satt in sonden i vätskan, varm eller kall, utifrån detta kan vi beräkna systemets tidskonstant. Först måste du identifiera var startpunkten och slutpunkten, startpunkten är spänningen innan du sätter sonden i vätskan och slutpunkten är när den löste sig. Därefter subtrahera dem och det är stegets spänningsförändring, testet du utförde var en stegändring som är en plötslig förändring av ingången till ett system, steget är temperatur. Gå nu till din graf på 63,2% av spänningsförändringen och den här tiden är tidskonstanten.

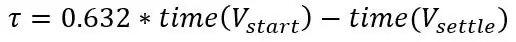
Om du ansluter det värdet till överföringsfunktionen har du sedan formeln för att beskriva systemens frekvenssvar men det är inte det vi vill ha just nu, vi vill ha den faktiska temperaturen vid tidpunkten t för ett steg i temperaturen så vi går att behöva utföra en omvänd Laplace -omvandling av ett steg in i systemet. Överföringsfunktionen för ett första ordningssystem med inmatning av ett steg är följande:

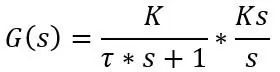
Där Ks är stegstorleken, dvs. temperaturskillnaden. Så låt oss säga att sonden är bunden till 20 grader C, placerad i vatten vid 30 grader C och sonden har en tidskonstant på 8s, överföringsfunktionen och tidsdomänformeln är följande:

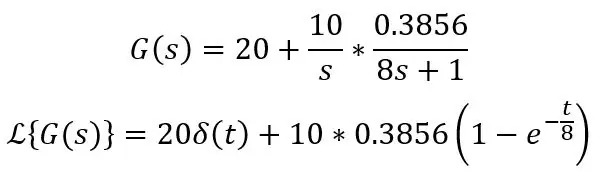
Δ (t) betyder bara en impuls dvs DC -förskjutning på 20 grader C i det här fallet, du kan bara skriva 20 i dina ekvationer när du beräknar detta. Detta är standardekvationen för steget in i ett första ordningssystem:

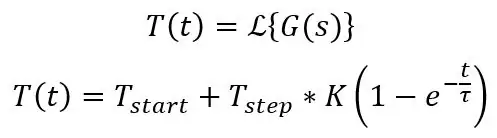
Ovanstående beräknar temperaturen vid tidpunkten t men detta fungerar för spänningen eftersom de är proportionella mot varandra, du behöver bara start- och slutvärdet, tidskonstant och stegstorlek. En webbplats som heter Symbolab är utmärkt för att kontrollera om din matte stämmer, den kan göra Laplace, integration, differentiering och massor av andra saker och det ger dig alla steg på vägen. Den omvända Laplace -transformen ovan kan hittas här.