Bioimpedansanalys (BIA) Med AD5933: 9 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:44

Jag har varit intresserad av att göra en bioimpedansanalysator för mätningar av kroppssammansättning och mina slumpmässiga sökningar fortsatte att hitta en design från klassen Biomedical Instrumentation 2015 vid Vanderbilt University. Jag har arbetat igenom designen och förbättrat den något. Jag skulle vilja dela med mig av mina fynd. Ta det du kan använda från denna "genomgång" om något inte är klart föreslå förbättringar. Jag kan en dag skriva min tanke i en mer sammanhållen form, men för nu hoppas jag att du kan använda vad du än ser här. (Om du tror att du kan skriva upp detta och förbättra det är du välkommen)

Nalle

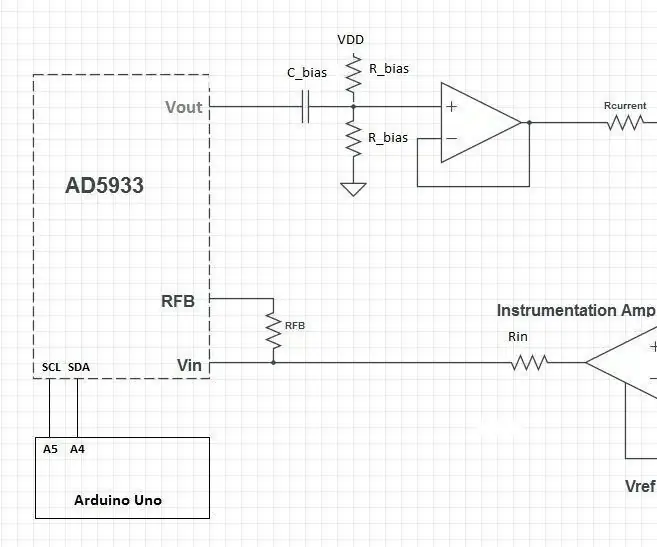
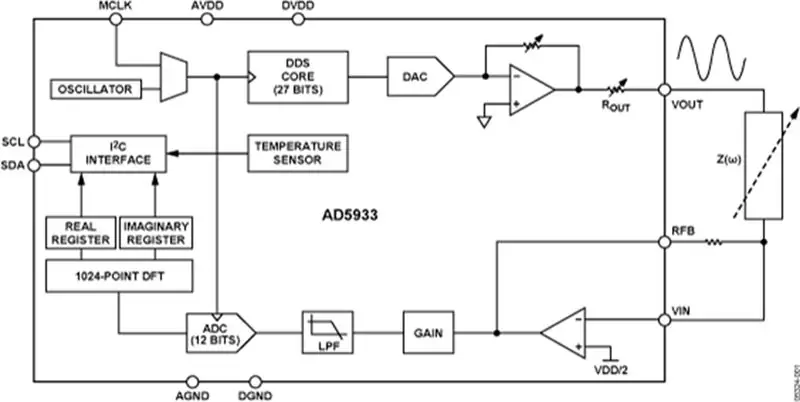
Denna design består av AD5933-chipet och en anpassad analog front-end (AFE) för att koppla ihop AD5933 med kroppen. AD5933 mäter sedan och resultaten kan sedan bearbetas av en mikrokontroller (t.ex. en Arduino).

Om du planerar att använda Arduino som strömförsörjning, se till att drift- och instrumentförstärkarna (op-ampere och in-ampere) stöder så kallade "single supply" -spänningar och har spår-till-rail-specifikationer.

(I det följande kommer jag att använda en strömförsörjning (från en Arduino) på 5V och inställningen Range 1 på AD5933.)

Steg 1: Re-bias-scenen

Den första delen av AFE är ett omspänningsskede. Utspänningssignalen är inte centrerad i mitten av matningsspänningsområdet (VDD/2). Detta korrigeras genom att använda en kondensator för att blockera DC -delen av signalen och skicka den via en spänningsdelare för att lägga till en DC -förskjutning tillbaka i signalen.

De två återförspänningsmotstånden kan ha valfritt värde så länge de är desamma. Det specifika värdet av locket är inte heller viktigt.

Re-bias-scenen fungerar som ett högpassfilter och har därför en gränsfrekvens:

f_c = 1 / (2 * pi * (0,5 * R) * C)

Se till att gränsfrekvensen är några decennier under den lägsta frekvens du planerar att använda. Om du planerar att använda 1 kHz i din applikation bör du välja kapslar och motståndsvärden som ger dig en gränsfrekvens i storleksordningen 1-10 Hz.

Den sista delen av detta steg är en op-amp som är inställd för att vara en spänningsföljare. Detta för att se till att motståndsvärdena inte stör nästa steg

Steg 2: Strömavkänningsmotstånd

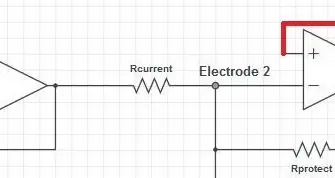
Den första delen av nästa steg är det nuvarande avkänningsmotståndet. Strömmen genom detta motstånd kommer att vara samma ström som förstärkaren kommer att försöka behålla genom kroppen. Se till att strömmen överensstämmer med säkerhetsstandarderna IEC6060-1*:

Under frekvenser på 1 kHz tillåts högst 10 microAmps (RMS) genom kroppen. Vid frekvenser över 1 kHz ger följande ekvation den högsta tillåtna strömmen:

Max AC -ström <(minsta frekvens i kHz) * 10 microAmps (RMS)

Förhållandet mellan toppamplituden för en AC -signal och dess RMS -värde är: Peak = sqrt (2) * RMS. (10 microAmps RMS motsvarar 14 microAmps toppamplitud)

Med hjälp av Ohms Law på motståndet kan vi beräkna motståndsvärdet som uppfyller säkerhetsstandarden. Vi använder excitationsspänningen från AD5933 och maxströmvärdet:

U = R * I => R = U / I

T.ex. med inställningen Range 1 Upeak = 3V / 2 = 1,5V (eller 1V @3,3V)

Genom att använda 14 microAmp -toppvärdet ovanifrån får jag ett motståndsvärde på minst 107kOhms

Referenser:

* Analoga enheter: "Bio-impedanskretsdesign för kroppsslitna system"

Steg 3: Trans-konduktansförstärkaren

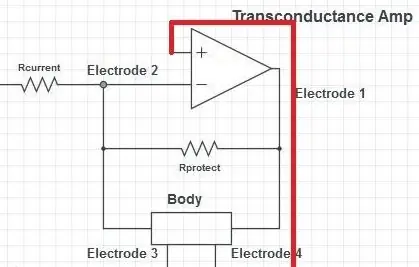
Efter den aktuella avkänningsmotståndaren finns en op-amp i en negativ feedback-konfiguration. Detta är en så kallad Load-in-the-Loop-installation. Den positiva ingången på op-amp är ansluten till en VDD/2-spänning. Op-amp kommer nu att försöka justera sin utsignal i motsatt riktning till excitationssignalen så att spänningen vid den negativa terminalen blir lika med VDD/2. Detta kommer att producera en vipppotential som driver och drar strömmen genom kroppen.

Strömmen från op-amp: s negativa terminal är praktiskt taget noll. All ström genom det strömavkännande motståndet måste därför flöda genom kroppen. Detta är mekanismen som gör denna inställning till en trans-konduktansförstärkare (även kallad en spänningsstyrd strömkälla, VCCS).

Op-amp kan bara behålla strömmen om kroppens impedans inte är för hög. Annars skulle op-amp-utgången bara maxas ut vid matningsspänningen (0 eller 5 V). Det maximala spänningsspannet som kan upprätthållas är VDD/2 + Upeak (2,5 + 1,5V = 4V @ 5V matning). Spänningsmarginalerna för op-förstärkaren bör subtraheras från detta värde, men om op-amparen har spår-till-skena-specifikationer skulle det bara vara en liten mängd. Den maximala impedansen som op-amp kan driva är därför:

Z <(VDD / 2 + Upeak) / Imax

(I min inställning Z <4V / 14 microAmps = 285 kOhms, önskan är mycket för att täcka kroppens impedansområde)

Skyddsmotståndet har ett mycket stort värde (1-1,5 MOhms) jämfört med kroppen (cirka 100kOhms) och för alla normala operationer kommer detta inte att dra någon märkbar ström och parallellanslutningens impedans domineras av kroppens impedans. Om kroppens impedans skulle stiga (t.ex. kuddar som lossnar) kan strömmen sedan gå genom motståndet och maximering av op-förstärkaren skulle inte skapa obehagliga spänningar i kuddarna.

Steg 4: Instrumentförstärkaren

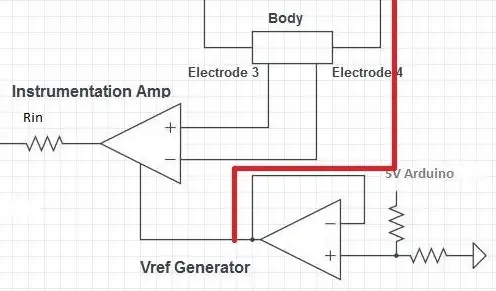
Nästa steg är instrumentationsförstärkaren (in-amp) som mäter spänningen över kroppen. Spänningen över kroppen oscillerar runt 0V, men AD5933 behöver ingångsspänningen för att vara i ett positivt område. Förstärkaren lägger därför till en DC-förskjutning av VDD/2 till den uppmätta spänningssignalen.

VDD/2 -referensen genereras av en spänningsdelare. Vilket värdemotstånd som helst kan användas så länge de är desamma. Spänningsdelaren separeras från impedansen för resten av kretsen av en spänningsföljare. Spänningsföljarens utgång kan sedan vidarebefordras till både förstärkaren och trans-konduktansförstärkaren.

Steg 5: Ingångssteg och kalibrering

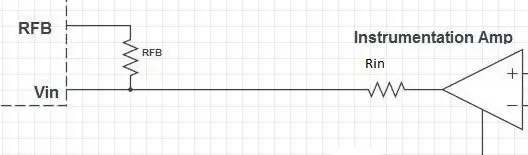
Ingångssteget för AD5933 innehåller en op-amp i negativ feedback-konfiguration. Det finns två motstånd: ett i serie (Rin) och ett parallellt (RFB). Förstärkningen av op-amp ges av

A = - RFB / Rin

Vinsterna hos ingångsförstärkaren och in-förstärkaren (och PGA) måste se till att signalen som går in i ADC på AD5933 alltid är inom 0V och VDD.

(Jag använder en enhetsförstärkning i förstärkare och motståndsvärden som ger ca A = 0,5)

Inuti AD5933 kommer ADC att omvandla spänningssignalen till a till en digital signal. Spänningsområdet från 0V till VDD omvandlas till det digitala området 0-128 (2^7). (Dokumentationen är inte klar om detta men en noggrann undersökning av tomterna i [1] och några experiment från min sida bekräftar detta.)

Inuti DFT -modulen finns det ytterligare en skala på 256 (1024/4, se [1]) innan resultatet sparas i det verkliga och imaginära registret.

Genom att följa spänningssignalen genom AFE, in i ADC och använda skalfaktorerna som nämnts innan är det möjligt att uppskatta förstärkningsfaktorn till:

g = (VDD * Rström * Rin) / (256 * PGA * Upeak * RFB * 2^7)

viss kalibrering kan fortfarande vara nödvändig, så ta hänsyn till vissa effekter som inte ingår i denna matematiska modell, så mät det verkliga förstärkningsvärdet genom att mäta komponenter med känd impedans, som motstånd. (g = Z / mag, se nedan)

Impedansen kan nu beräknas med

Z = g * mag

mag = sqrt (verklig^2 + imaginär^2)

PA = arctan2 (verklig, imaginär) - deltaPA

PA behöver förmodligen kalibreras liksom det finns en systematisk fasförskjutning som en funktion av frekvens i AD5933. deltaPA kommer förmodligen att vara någon linjär frekvensfunktion.

Motståndet och reaktansen kan nu beräknas med

R = Z * cos (PA)

X = Z * sin (PA)

Referenser: [1] Leonid Matsiev, "Förbättra prestanda och mångsidighet för system baserade på enkelfrekventa DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

Steg 6: Advanced Stuff: Spectral Leakage (DC)

Signalen som vi lägger in i AD5933 är en spänning/ström som en tidsfunktion, men vårt främsta intresse är impedansen som en funktion av frekvens. För att konvertera mellan tidsdomän och frekvensdomän måste vi ta Fourier-transformen av tidsdomänen. AD5933 har en inbyggd diskret Fourier-transform (DFT) -modul. Vid låga frekvenser (under cirka 10 kHz) påverkas inbyggnaden i DFT av aliasing och spektralläckage. I [1] går han igenom matematiken om hur man korrigerar spektralläckaget. Kärnan i detta är att beräkna fem (plus två) konstanter för varje frekvenssteg i svepet. Detta kan enkelt göras t.ex. av Arduino i programvara.

Läckaget kommer i två former: ett DC -läckage som är additivt i naturen och ett AC -läckage som är multiplikativt.

DC -läckaget härrör från det faktum att spänningssignalen vid ADC inte oscillerar runt 0V utan runt VDD/2. En DC -nivå på VDD/2 bör motsvara en digital DC -avläsning på cirka 64 (betecknat delta i [1]).

Stegen för att korrigera DC -spektralläckaget:

1) Beräkna kuvertfaktorn E för den aktuella frekvensen.

2) Beräkna de två förstärkningsfaktorerna GI (real) och GQ (imaginär)

3) subtrahera delta * GI från värdet på det verkliga registret och delta * GQ från värdet på det imaginära registret

Referenser:

[1] Leonid Matsiev, "Förbättra prestanda och mångsidighet i system baserat på

Enfrekventa DFT-detektorer som AD5933 , Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mått. Syst., Vol. XXII (2015), nr 1, s. 13–24.

Steg 7: Advanced Stuff: Spectral Leakage (AC)

Liksom DC -läckaget kan AC -läckaget korrigeras matematiskt. I [1] kallas resistansen och reaktansen A*cos (phi) respektive A*sin (phi), där A motsvarar impedansens storlek och phi motsvarar fasvinkeln (PA).

Stegen för att korrigera AC -spektralläckaget:

1) Beräkna kuvertfaktorn E (inte samma som för DC) för den aktuella frekvensen.

2) Beräkna de tre faktorerna a, b och d. (cirka värden vid högre frekvenser: a = d = 256 och b = 0)

3) Motstånd (Acos (phi)) och reaktans (Asin (phi)) kan nu beräknas i digitala enheter

Referenser: [1] Leonid Matsiev, "Förbättra prestanda och mångsidighet för system baserade på enkelfrekventa DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mått. Syst., Vol. XXII (2015), nr 1, s. 13–24.

Steg 8: Avancerade saker: den teoretiska förstärkningsfaktorn

Med tanke på den matematiska modelleringen av DFT bör det också vara möjligt att modellera hela AFE matematiskt. Matematiskt kan spänningssignalen beskrivas med en sinusfunktion med en given fast frekvens, en DC -offset och en AC -oscillation med en toppamplitud. Frekvensen ändras inte under ett frekvenssteg. Eftersom förstärkningsfaktorn bara ändrar storleken på impedansen och inte PA kommer vi här inte att vara bekymrade över något fasskift som induceras på signalen.

Här är en kort sammanfattning av spänningssignalen när den sprider sig genom AFE:

1) Efter omspänningssteget är AC-amplituden fortfarande Upeak = 1,5V (1V @ VDD = 3,3V) och DC-offset har ändrats till VDD/2.

2) I strömavkänningsmotståndet är spänningen tyst samma som föregående steg …

3) … men på grund av vippspänningen hos op-amp har AC-svängningarna storleken Z*Upeak/Rcurrent. (DC -förskjutningen avbryts av op -ampere -referensspänningen för VDD/2 - vippens vridpunkt - och blir en kraftig mark i denna del av kretsen)

4) Enhetsförstärkaren lägger till DC-förskjutningen för VDD/2 tillbaka in och vidarebefordrar signalen till ingångssteget för AD5933

5) Op-amp i ingångssteget har en förstärkning på A = -RFB/Rin och AC-amplituden blir därför (Z*Upeak/Rcurrent)*(RFB/Rin)

6) Strax före ADC finns en programmerbar förstärkningsförstärkare (PGA) med två inställningar en förstärkning på 1 eller 5. Spänningssignalen vid ADC blir därför: PGA*(Z*Upeak/Rcurrent)*(RFB/Rin)

ADC omvandlar v (t) -signalen till en digital signal x (t) = u (t) / VDD * 2^7 med en 12 -bitars noggrannhet.

Storleken A är ansluten till impedansen Z med förstärkningsfaktorn, k, som A = k * Z och har ett ungefärligt värde av k = PGA * Upeak * RFB * 2^7 / (VDD * Rcurrent * Rin).

Om du gillar att arbeta med gain-faktor istället g = 1 / k och Z = g * A.

Steg 9: Avancerade saker: PA -skiftet

I [2] hittar de ett systematiskt skift i PA som en funktion av frekvensen. Detta beror på en tidsfördröjning mellan DAC där excitationssignalen genereras och DFT där den inkommande signalen måste slingras med den utgående signalen.

Skiftet kännetecknas av antalet klockcykler signalen är fördröjning mellan DAC och DFT internt i AD5933.

Referenser: [1] Leonid Matsiev, "Förbättra prestanda och mångsidighet för system baserade på enkelfrekventa DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mått. Syst., Vol. XXII (2015), nr 1, s. 13–24.