Grid Tie Inverter: 10 steg (med bilder)

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:40

Detta är ett köttfullt projekt så spänn ihop!

Inverterare med nätanslutning gör att du kan trycka in strömmen i ett vägguttag, vilket är en fantastisk förmåga. Jag tycker att kraftelektroniken och styrsystemen som är involverade i deras design är intressanta så jag byggde min egen. Denna rapport delar med mig av vad jag lärt mig och dokumenterar hur jag gjorde saker. Jag skulle vara intresserad av alla kommentarer du hade (förutom de om att inte krångla till elnätet).

Alla begrepp är skalbara men denna inställning hade en maximal effekt på 40 watt innan filterinduktorerna började mättas. Utgångsströmmen var sinusformad med THD <5%.

Se programvaran på min GitHub

Tillbehör

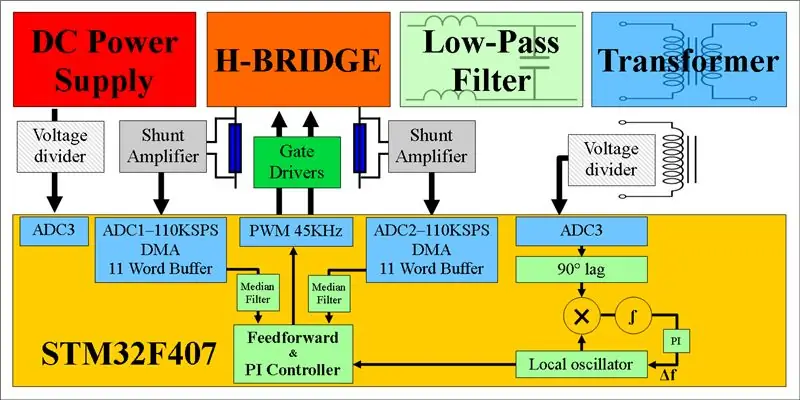
• Jag använde utvecklingsbordet STM32F407. Den körs på 168 MHz och har 3 inbyggda ADC: er som kan upplösas med 12 bitar på över 2,4 MSPS (miljonprover per sekund) vardera. Det är sinnessjukt!
• Jag använde utvecklingsbrädan DRV8301. Detta rymmer en 60v H-Bridge tillsammans med nödvändiga gate-drivrutiner, ström shunts och ström shunt förstärkare. Supertrevlig!
• Jag använde en toroidformad transformator 230-25v med 2 utgångskranar. Detta innebar att jag inte behövde producera nätspänning direkt utan kunde arbeta med toppspänningar på 40 volt istället. Mycket säkrare!
• Jag kopplade ihop en mängd induktorer och kondensatorer för att få de L- och C -värden som jag ville ha för filtret.
• Ett oscilloskop och differentialsond är nyckeln för ett projekt som detta. Jag har ett Picoscope

Steg 1: Vad är nätström?

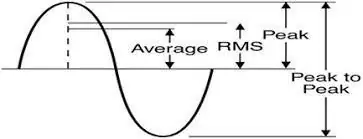
Vad du får vid ett eluttag (i Storbritannien) är en 50Hz 230v RMS sinusformad signal med en mycket låg impedans. Några saker att säga om det:

50Hz - Nätfrekvensen bibehålls mycket exakt vid 50Hz. Det varierar något men 90% av tiden är det mellan 49,9-50,1Hz. Kolla här. Du kan tänka dig att alla enorma generatorer i kraftverk upp och ner i landet snurrar i samklang. De roterar synkront och producerar en sinusformad signal på 50 Hz för oss. Deras kombinerade massiva rotationströghet tar tid att sakta ner eller påskynda.

I teorin, om en enorm belastning var ansluten till nätet skulle det börja sakta ner landets generatorer. Men som svar skulle killarna i National Grids kontrollkontor begära att kraftstationerna skulle steka sina pannor, skruva upp värmen och tvinga dessa generatorer svårare att hänga med i efterfrågan. Således är utbud och efterfrågan i en kontinuerlig dans med varandra.

Ytterligare en sak att säga om 50Hz -signalen. Även om det varierar väldigt lite om 50Hz, ser killarna i toppen till att medelfrekvensen under dagen är exakt 50Hz. Så om nätet ligger på 49,95 Hz i 10 minuter, kommer de att se till att det körs på 50,05 Hz senare för att få det exakta antalet cykler till 50 Hz x 60 sekunder x 60 minuter x 24 timmar = 4, 320 000/dag. De gör detta exakt med hjälp av International Atomic Time. Hushålls-, kontors- och industriapparater kan därför använda nätfrekvensen för att hålla tid. Detta görs vanligtvis med exempelvis mekaniska sockeltimrar.

230v - Detta är RMS -spänningen (Root Mean Square) för 50Hz -signalen. Själva signalen svänger upp till en 325v topp. Detta är viktigt att veta för att om du bygger en växelriktare måste du producera så höga spänningar om du ska få ström att strömma in i kontakterna.

I verkligheten är spänningarna som ses vid en kontakt i ditt hus ganska varierande. Det beror på spänningsfall över motståndet i ledningar, kontakter, säkringar, transformatorer etc. Det finns motstånd överallt. Om du slår på en elektrisk dusch som drar 11 kilowatt (det är ~ 50 ampere) kommer även 0,2 ohm motstånd att tappa dig 10 volt. Du kanske ser det här som att lamporna dämpas så lite. Stora motorer, som de i hoover drar enorma strömmar medan motorn får fart. Så du ser ofta en liten flimmer av lamporna när du tänder dem.

Min poäng är att nätspänningen är mycket mer variabel. Här i Storbritannien ska det vara 230v med en +10%/-6% tolerans. Du kan förvänta dig att se plötsliga förändringar och fluktuationer när stora laster i närheten slås på/av. Tänk torktumlare, vattenkokare, ugnar, hoovers etc.

Sinusformad - Signalen ska vara en fin ren sinusvåg men i verkligheten suger vissa icke -linjära apparater sin kraft från vissa punkter i sinusvågscykeln. Detta introducerar distorsion och det är därför signalen inte är en perfekt sinusvåg. Icke linjära belastningar inkluderar vanligtvis datorns strömförsörjningar, lysrör, laddare, TV -apparater etc.

Total harmonisk distorsion (THD) kvantifierar detta i vågformen. Det finns regler för hur ren en växelriktares utgång måste vara. Om den inte kan producera en tillräckligt ren signal kommer den inte att godkännas för försäljning. Detta är viktigt eftersom harmoniskt innehåll i nätet minskar effektiviteten hos vissa enheter som är anslutna till det (särskilt udda övertoner). Jag tror att den högsta tillåtna THD är 8%

Låg impedans - När du tänker på en växelriktare är detta viktigt att tänka på. Det finns alla slags belastningar anslutna till elnätet, inklusive induktiva, resistiva och ibland kapacitiva laster. Så impedansen är okänd och föränderlig. Motståndet är mycket litet, vilket betyder att om du ansluter en hög strömbelastning kommer spänningen inte att sjunka mycket alls.

Steg 2: Hur man skjuter kraften i nätet

För att driva in strömmen i nätet måste vi syntetisera en signal som exakt matchar nätets frekvens och fas men med en något högre spänning.

På grund av nätets låga motstånd är det svårt att veta exakt hur mycket högre att göra den spänningen. Och eftersom RMS -spänningen fluktuerar måste vi se till att vi fluktuerar med den. Bara att producera en fast 50Hz spänningssignal något högre än nätspänningen kommer inte att fungera!

PI Styrning av utströmmen

Vad vi behöver är en styrslinga där vi mäter den momentana ström vi trycker in i nätet och justerar automatiskt vår utspänning för att driva den ström vi vill ha. Detta kommer effektivt att omvandla vår effekt till en strömkälla (snarare än en spänningskälla) som är mer lämplig för att driva låga impedanser. Vi kan uppnå detta genom att använda en PI (Proportional Integral) styrslinga:

PI -kontrollöglor är fantastiska! Det finns 3 delar till dem:

• Det uppmätta värdet - den ström vi lägger i elnätet
• Börvärdet - den ström vi vill driva in i elnätet
• Utgången - Signalspänningen som ska genereras

Varje gång vi anropar PID -algoritmen passerar vi den senaste strömmätningen och det börvärde vi vill ha. Det returnerar ett godtyckligt tal (proportionellt mot utspänningen som ska genereras).

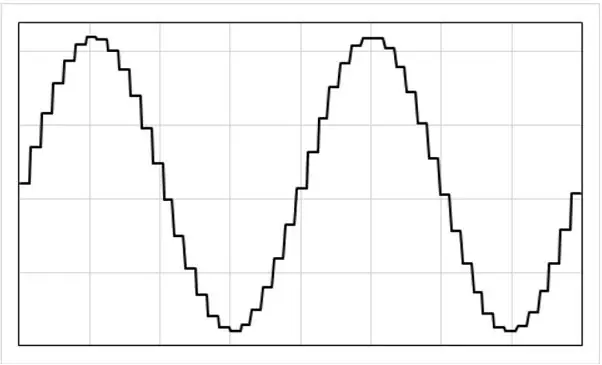
Vår PID -kontrollalgoritm gör att vi kan välja utströmmen vi vill ha vid ett givet tillfälle. För att producera en 50 Hz sinusformad utström måste vi kontinuerligt ändra vår begärda ström på ett sinusformat sätt.

PID -algoritmen anropas var 100us (motsvarande 200 gånger per 50Hz -cykel). Varje gång den kallas kan den göra direkta justeringar av utspänningen och därmed indirekt justera utströmmen. Som ett resultat producerar vi en stegvis utström som liknar den som visas på bilden med varje steg som inträffar var 100us. Det ger tillräckligt med upplösning.

Feedforward -kontroll

Vi kan massivt minska arbetsbelastningen för PI -regulatorn genom att lägga till en feedforward -controller också. Det här är lätt! Vi vet den ungefärliga utspänningen vi behöver generera (samma som den momentana nätspänningen). PI -styrenheten kan sedan lämnas för att lägga till den lilla extra spänning som behövs för att driva en utström.

I sig själv anpassar frammatningsregulatorn växelriktarens utspänning till nätets spänning. Ingen ström ska flöda om vi matchar tillräckligt bra. Feedforward -kontrollen gör därför 99% av utmatningskontrollen.

På grund av nätets låga motstånd skulle alla skillnader i vår FF -utspänning och nätspänningen resultera i en stor ström. Jag lade därför till ett 1ohm buffertmotstånd mellan växelriktaren och nätet. Detta leder till förluster, men de är ganska små i det stora systemet.

Steg 3: Producera utspänningen med PWM

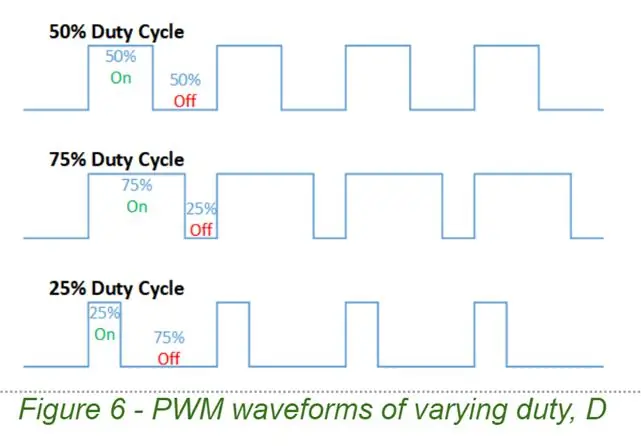
Även om vi indirekt styr utströmmen är det en utspänning som vi genererar vid varje givet tillfälle. Vi använder PWM (Pulse Width Modulation) för att producera vår utspänning. PWM-signaler kan enkelt produceras av mikrokontroller och de kan förstärkas med en H-Bridge. De är enkla vågformer som kännetecknas av två parametrar, frekvensen F och arbetscykeln D.

En PWM -vågform växlar mellan 2 spänningar, i vårt fall 0v och Vsupply

• Med D = 1,0 är PWM -vågformen helt enkelt DC vid Vsupply
• Med D = 0,5 får vi en fyrkantvåg med en medelspänning på 0,5 x Vsupply, (dvs D x Vsupply)
• Med D = 0,1 får vi en pulsad vågform med ett periodmedelvärde på 0,1 x Vsupply
• Med D = 0,0 är utgången en flatlinje (DC vid 0v)

Medelspänningen är det viktigaste. Med ett lågpassfilter kan vi ta bort allt utom DC-genomsnittskomponenten. Så genom att variera PWM -arbetscykeln D kan vi göra vilken önskad likspänning som helst. Ljuv!

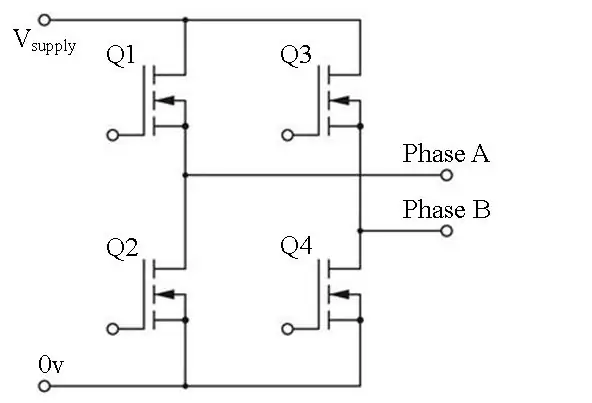
Anställa en H-Bridge

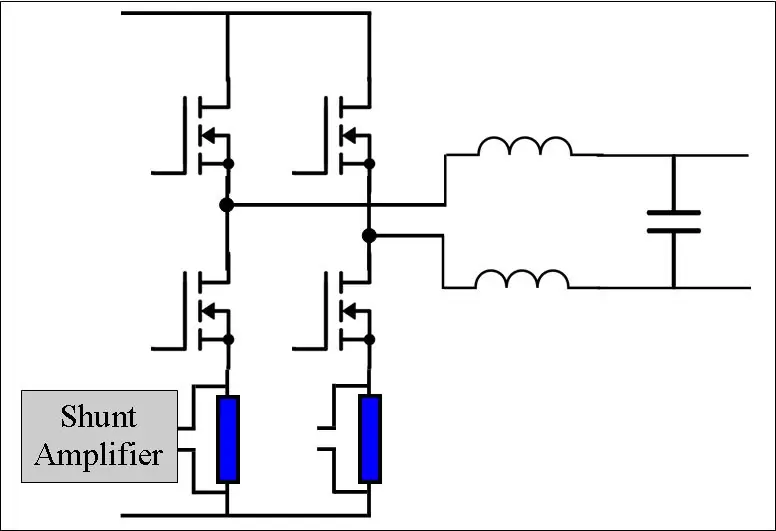
En H-bro består av 4 kopplingselement. Dessa kan vara BJT, MOSFET eller IGBT. För att producera den första halvan (0 - 180 grader) av sinusvåg, ställer vi in fas B låg genom att stänga av Q3 och Q4 (dvs. applicera PWM med D = 0). Vi utför sedan vår PWMing på fas A. För andra halvan, där VAB är negativt, sätter vi fas A låg och applicerar vår PWM på fas B. Detta kallas bipolär omkoppling.

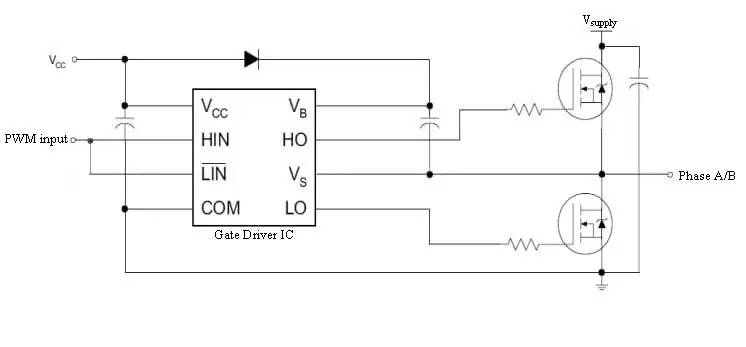
MOSFET: erna i H-bron måste drivas av en grindförare. Detta är ett eget ämne men ett enkelt chip kan ta hand om det. DRV8301 dev-bräda rymmer bekvämt H-bron, grindförare och nuvarande shuntar för oss som gör detta projekt mycket enklare.

Steg 4: Mät ström

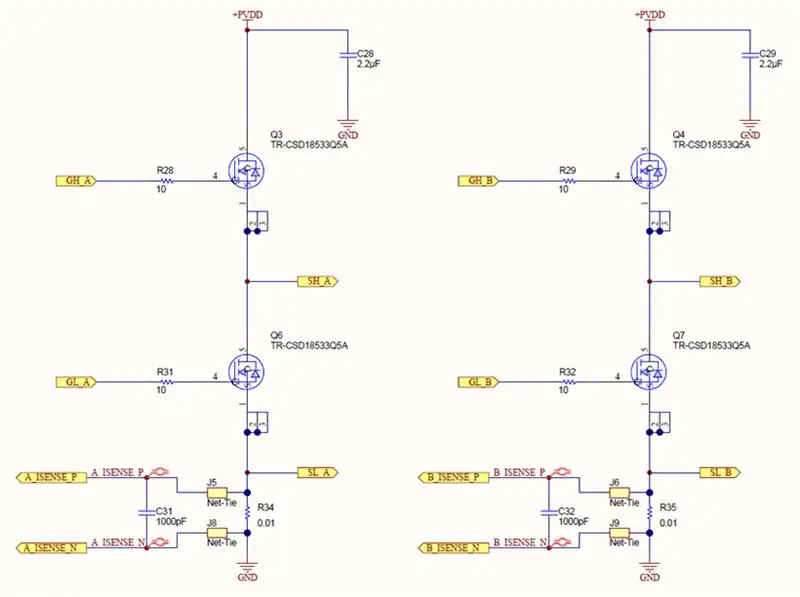
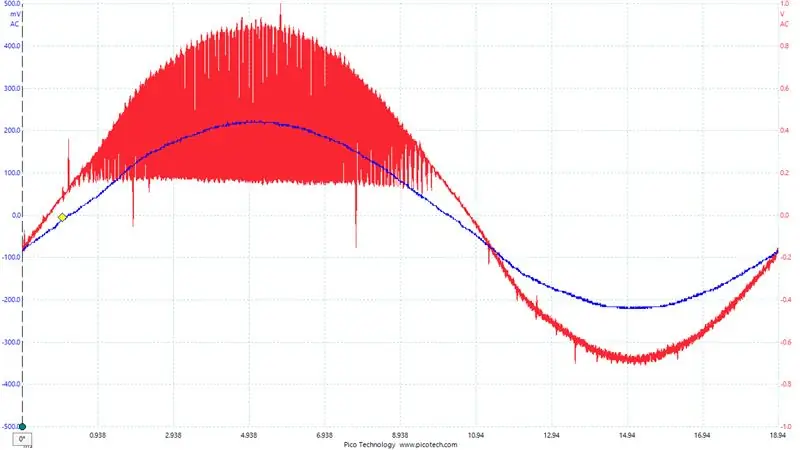
Varje ben på H-bron har ett shuntmotstånd och en differentialförstärkare. Våra shuntar är 0,01 ohm och våra förstärkare är inställda på en förstärkning på 40. Därför utvecklar 1 Amp 10 mV över shunten som därefter förstärks till 400 mV.

Utsignalerna från shuntförstärkarna läses av 12 -bitars ADC: erna på STM32F407 som körs i kontinuerligt konverteringsläge. ADC: erna är inställda för att prova varje shunt vid 110KSPS och DMA -styrenheten skriver automatiskt omvandlingarna till en cirkulär buffert med 11 ord i RAM. När en aktuell mätning önskas kallar vi en funktion som returnerar medianvärdet för denna 11 ords buffert.

Eftersom vi begär strömmätningar varje PID -iteration (vid 10KHz) men fyller våra 11 -ords ADC -buffertar med en hastighet av 110KHz, bör vi få helt färska data för varje PID -iteration. Anledningen till att använda ett medianfilter är att PWM -växling kan införa spikar i blandningen och medianfilter utraderar falska ADC -prover mycket effektivt.

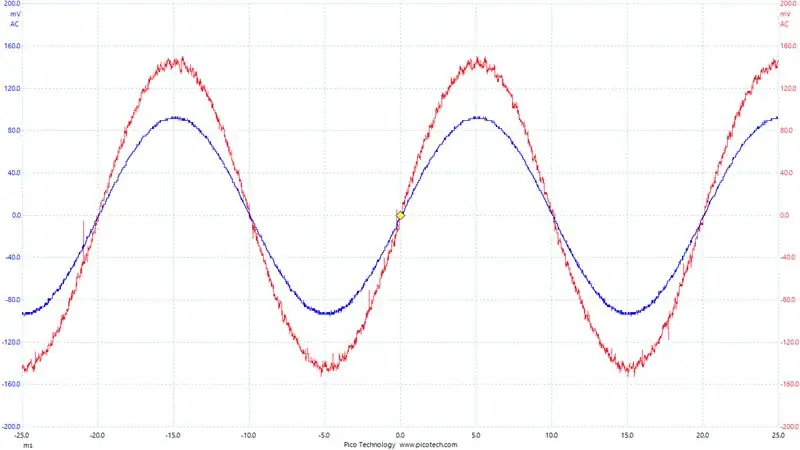
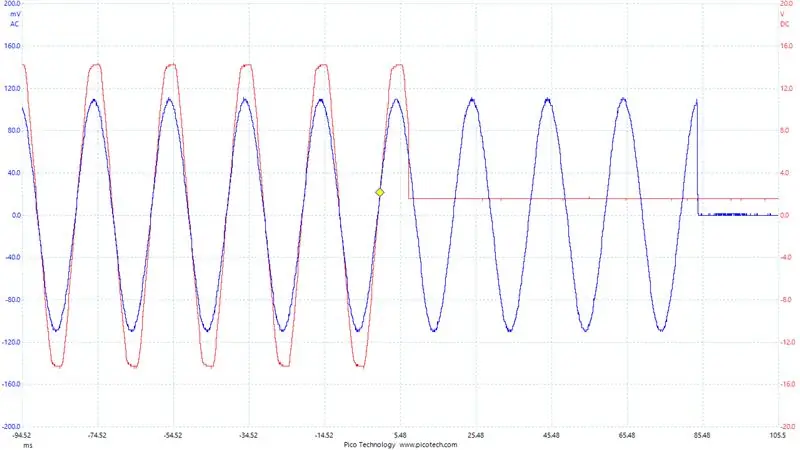
En viktig punkt att ta upp här: Vilket ben på H-bron använder vi för strömmätningar? Det beror väl på vilket ben vi för närvarande PWMing och som bara hålls lågt. Benet som hålls lågt är det vi vill mäta vår ström utifrån eftersom strömmen alltid flyter genom shuntmotståndet på den sidan. I jämförelse, på sidan som är PWMed, när högsidan MOSFET är på och lågsidan är av, strömmar ingen ström genom lågsidans shunt. Så vi ändrar vilket ben vi mäter ström på baserat på omriktarens utgångspolaritet. Du kan se detta tydligt på bilden och visar utsignalen från en av shuntförstärkarna under en period. Uppenbarligen vill vi ta avläsningar under den släta biten.

För att hjälpa till att felsöka våra nuvarande avläsningar. Jag satte upp Digital-till-analog-omvandlaren på STM32F407. Jag skrev de aktuella avläsningarna jag fick och omfattade utmatningen. Du kan se detta i den sista bilden, det blå är spänningen över utgångsbuffertmotståndet (dvs. utströmmen/1,1 ohm) och den röda signalen är vår DAC -utgång.

Steg 5: Filtrering av utdata

Utmatningsfiltret är en viktig del i designen. Vi behöver dessa egenskaper från det:

1. Blockera alla högfrekventa växlingar men passera en 50Hz signal
2. Låga förluster
3. För att inte resonera!
4. För att hantera de strömmar och spänningar som är inblandade

Fouriertransformationen av en PWM -signal med frekvens F, Driftcykel D, mellan 0 - Vsupplysspänning är: (D x Vsupply) + Sinusvågor vid grundfrekvensen F och övertoner därefter

Det här är lysande! Det betyder att om vi sätter vår PWM -signal genom ett lågpassfilter som blockerar PWM -fundamentet och allt ovan. Vi är precis kvar med likspänningstiden. Genom att variera arbetscykeln kan vi enkelt producera vilken spänning vi vill mellan 0 - Vsupply som förklaras.

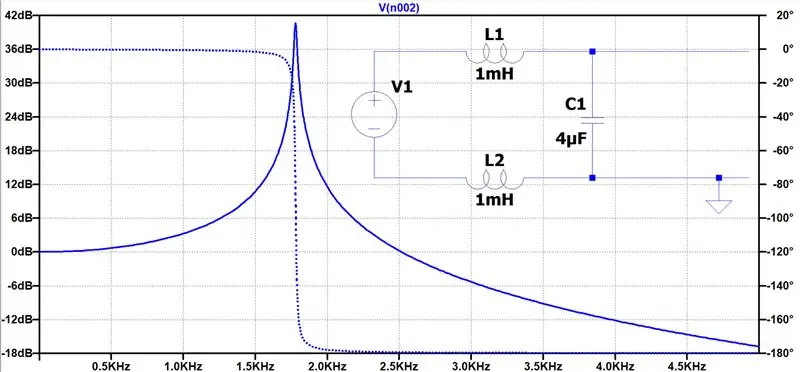
Baserat på de önskade egenskaperna som nämns ovan kan vi designa utgångsfiltret. Vi behöver ett lågpassfilter med minimalt motstånd för att undvika förluster. Därför använder vi bara induktorer och kondensatorer. Om vi väljer en resonansfrekvens mellan 1 - 2KHz kommer vi att undvika resonans eftersom vi inte injicerar några signaler nära den frekvensen. Här är vår filterdesign. Vi tar vår effekt som spänningen över C1.

Genom att välja L1 = L2 = 440uH, C1 = 8.4uF beräknar vi en resonansfrekvens på 1.85KHz. Det här är också realistiska komponentvärden.

Det är viktigt att se till att våra induktorer inte börjar mätta vid de strömmar vi förväntar oss. De induktorer jag har använt har en 3A mättnadsström. Detta kommer att vara den begränsande faktorn för vår krets uteffekt. Kondensatorns spänningsvärde är också viktigt att tänka på. Jag använder lite 450v keramik vilket är väldigt överdrivet i det här fallet!

Bodeplot (för lite olika L/C -värden) har genererats med LTspice. Det visar oss den dämpning som orsakas av olika ingångsfrekvenser. Vi kan tydligt se resonansfrekvensen vid 1,8KHz. Det visar att en 50Hz -signal är nästan helt oförfalskad medan jag kan säga att en 45 KHz -signal dämpas med 54dB!

Så låt oss välja vår PWM -bärfrekvens till ~ 45KHz. Genom att välja högre PWM -bärfrekvenser kan filterfrekvensen göras högre. Det är bra eftersom det gör L- och C -värdena mindre. Det betyder mindre och billigare komponenter. Nackdelen är att högre PWM -omkopplingsfrekvenser introducerar större förluster i transistoromkopplarna.

Steg 6: Synkronisera fas och frekvens

Synkronisering med nätfas och frekvens är det som gör en växelriktare. Vi använder en digital implementering av en PLL (Phase Locked Loop) för att uppnå exakt fasföljning av nätsignalen. Vi gör detta genom att:

1. Provtagning av nätspänningen
2. Producerar en lokal sinusformad signal på 50 Hz
3. Jämför fasen mellan vår lokala signal och nätsignalen
4. Justera frekvensen för den lokala signalen tills fasskillnaden mellan de 2 signalerna är noll

1) Sampling av nätspänningen

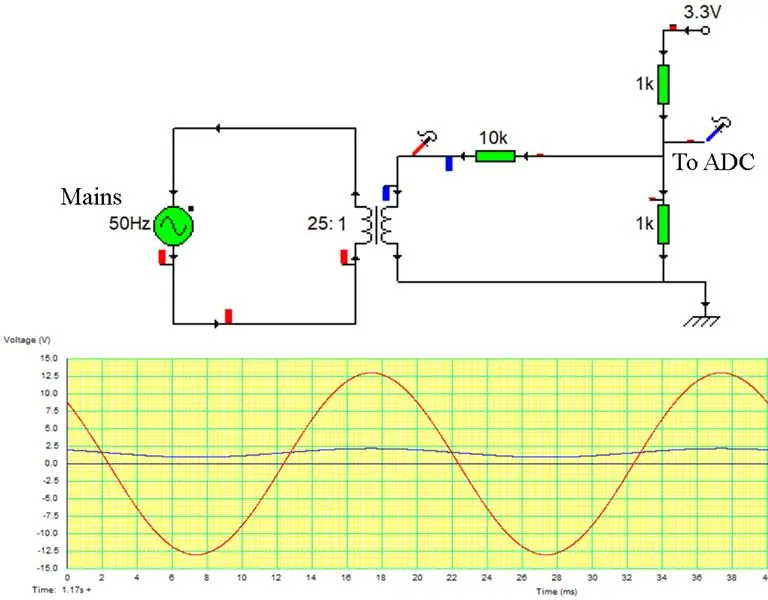
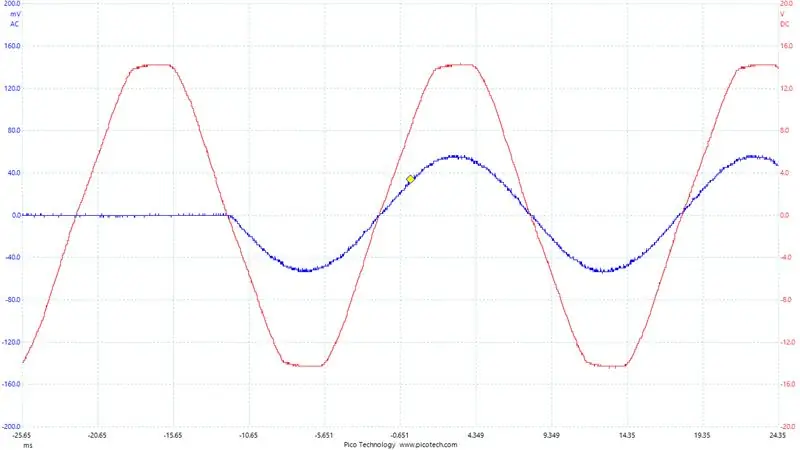
Vi konfigurerar en tredje ADC -kanal för att läsa av nätspänningen. Detta får vi genom att spänningsdela en transformatorkran som visas. Detta ger en skalad spänning som varierar omkring 1,65v som exakt representerar nätspänningen.

2) Att producera en lokal 50Hz sinusformad signal Det är enkelt att producera vår egen 50Hz sinusvåg. Vi lagrar en uppslagstabell med 256 sinusvärden. Vårt simulerade sinusvärde erhålls enkelt med hjälp av ett uppslagsindex som roterar stegvis genom tabellen.

Vi måste öka vårt index med exakt rätt hastighet för att få en 50Hz -signal. Nämligen 256 x 50Hz = 12, 800/s. Vi gör detta med hjälp av timer9 klockad på 168MHz. Genom att vänta 168MHz/12800 = 13125 klockfickor stegar vi vårt index i rätt takt.

3) Jämför fasen mellan vår lokala signal och nätsignalenDetta är den coola delen! Om du integrerar produkten av cos (vikt) x sin (vikt) under en period är resultatet noll. Om fasskillnaden är något annat än 90 grader får du ett nummer utan noll. Matematiskt:

Integral [Asin (t) x Bsin (t + φ)] = Ccos (φ)

Det här är bra! Det gör att vi kan jämföra nätsignalen, sin (ωt) med vår lokala signal, sin (⍵t + φ) och få ett värde.

Det finns dock en fråga som måste åtgärdas: Om vi vill att våra signaler ska förbli i fas måste vi justera vår lokala frekvens för att hålla Ccos (φ) termen maximal. Detta kommer inte att fungera särskilt bra och vi får dålig fasspårning. Detta beror på att d/dφ för ɑcos (φ) är 0 vid φ = 0. Det betyder att termen Ccos (φ) inte kommer att variera särskilt mycket med fasändringar. Låter det vettigt?

Det skulle vara mycket bättre att fasförskjuta den samplade nätsignalen med 90 grader så att den blir cos (ωt + φ). Då har vi detta:

Integral [Asin (t) Bcos (t + φ)] = Csin (φ)

Det är enkelt att införa ett 90 graders fasskift, vi sätter bara in våra ADC -spänningsprover i ena änden av en buffert och tar ut dem ett antal prover senare, vilket motsvarar ett fasskift på 90 grader. Eftersom nätfrekvensen knappast varierar från 50Hz fungerar en enkel tidsfördröjningsteknik strålande.

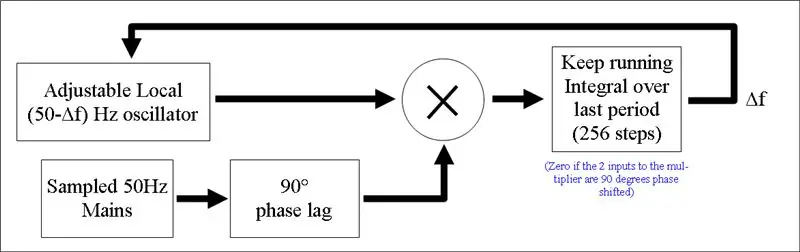
Vi multiplicerar nu vår 90 graders fasskiftade nätsignal med vår lokala signal och håller en löpande integral av produkten under den senaste perioden (dvs. över de senaste 256 värdena).

Resultatet vi vet blir noll om de två signalerna hålls exakt 90 grader från varandra. Detta är fantastiskt eftersom det ångrar fasskiftet vi just tillämpade på nätsignalen. Bara för att klargöra, istället för att maximera den integrerade termen försöker vi hålla den noll och vi fasförskjuter vår nätsignal. De 90 graders fasskift som införs av dessa 2 förändringar avbryter varandra.

Så om Integral_Result <0 vet vi att vi måste öka vår lokala oscillatorfrekvens för att få den tillbaka i fas med elnätet, och vice versa.

4) Justera frekvensen för den lokala signalen Den här biten är enkel. Vi justerar helt enkelt perioden mellan att öka med vårt index. Vi begränsar hur snabbt vi kan korrigera fasskillnaden i huvudsak filtrera bort falska whatevers. Vi gör detta med en PI -controller med en mycket liten I -term.

Och det är allt. Vi har låst vår lokala sinusvågscillator (som anger börvärdet för utgående ström) för att vara i fas med nätspänningen. Vi har implementerat en PLL -algoritm och den fungerar som en dröm!

Att öka frekvensen för vår lokala oscillator minskar också fasskiftet på nätsignalen. Eftersom vi begränsar frekvensjusteringen till +/- 131 fästingar (+/- ~ 1%) kommer vi att påverka fasförskjutningen med högst +/- 1 °. Detta kommer inte att spela någon roll medan faserna synkroniseras.

Teoretiskt sett skulle nätfrekvensen avvika med mer än 0,5 Hz förlora vårt faslås. Detta beror på ovanstående begränsning av hur mycket vi kan justera vår lokala oscillatorfrekvens. Det kommer dock inte att hända om inte nätet är på väg att misslyckas. Vårt skydd mot ön kommer att komma igång i alla fall.

Vi utför en nollkorsningsdetektering vid start för att försöka vårt bästa för att starta signalerna i fas från offset.

Steg 7: Anti-islanding

Wikipedia har en fantastisk artikel om öar och tekniker mot ön. Det innebär också att människor väser och klappar mer än nödvändigt när det gäller detta ämne. "Åh, du kan inte bygga din egen växelriktare, du kommer att döda någon osv."

Som förklaras bättre av wikipedia -artikeln använder vi ett par säkerhetsåtgärder som tillsammans ger tillräckligt skydd (enligt min mening):

1. Under-/överspänning
2. Under-/överfrekvens

Vi kan upptäcka dessa situationer genom att helt enkelt analysera vår samplade skalade nätspänning. Om något går ur spel, inaktivera H-bron och vänta på att saker och ting ska återgå till det normala.