3D -rekonstruktion från ett enda foto: 8 steg

2024 Författare: John Day | [email protected]. Senast ändrad: 2024-01-30 12:37

Uppgiften med 3D -rekonstruktion är vanligtvis förknippad med kikarsyn. Alternativt kan du flytta en enda kamera runt objektet. Under tiden, om objektets form är känd, kan uppgiften lösas från ett enda foto. Det vill säga att du bara har en kamera och den rör sig inte. Låt oss titta på hur du gör det steg för steg. Vi kommer att använda Rubiks kub eftersom den är väl standardiserad och har en rik uppsättning funktioner. Det kan ses som ett mycket enkelt föremål och samtidigt en komplicerad konstruktion. Så maskinsyn måste överstiga betydande hinder för att klara uppgiften.

Steg 1: Utvärdera uppgiftens komplexitet

Vid första anblicken är uppgiften enkel. Hitta den centrala knuten där 3 kanter på kuben kommer ihop och rita dessa kanter. Från deras koordinater är det möjligt att beräkna avståndet från kameran och rotationsvinklar. Problemet är att dessa rader inte finns. Från den vänstra bilden ser du att varje kant representeras av 2 parallella linjer. Vidare visar den övre högra bilden att var och en av dem är uppdelad i 3 segment. Dessutom, om vi tillämpar en variant av den populära Hough -transformationen som kan upptäcka linjesegment, utför den uppgiften med några fel som gör detektering av den centrala knuten omöjlig. Om ändarna inte når varandra finns det ingen enda punkt. Om detekteringen överskrider slutet kommer det att se ut som knuten i mitten av kanten som du ser på de 2 återstående bilderna.

Steg 2: Hitta rätt tillvägagångssätt

När för många detaljer gör deterministiska algoritmer omöjliga, är det dags att överväga ett probabilistiskt tillvägagångssätt. Om vi beräknar genomsnittsparametrarna för bilden kommer deras fel att minskas väsentligt och paradoxalt nog kommer metoden att bli mer tillförlitlig. Standard Hough -transformen matar inte ut linjesegment. Endast dess lutning theta och avståndet rho från koordinatets ursprung. De utgör Hough -rymddelen som visas ovan. Här motsvarar theta den horisontella axeln. Ljuspunkter markerar möjliga linjer på bilden. Observera att flera sådana platser ligger ovanför varandra. Inte konstigt, på vår bild finns det många parallella linjer. De har samma theta och olika rho.

Steg 3: Beräkna Theta Histogram

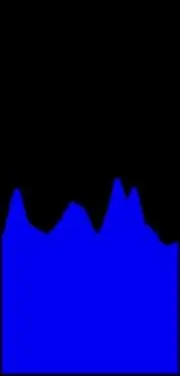
Låt oss upptäcka sådana kluster. För detta ändamål kommer vi att sammanfatta avläsningar för alla prickar i Hough -utrymmet med samma theta. Du ser motsvarande histogram på bilden. Några anteckningar om mätningar. När du arbetar med bilder i pixelkoordinater går X -axeln som vanligt, men Y pekar nedåt så koordinatets ursprung är det övre vänstra hörnet och theta ska mätas från X -axeln medurs. Med tanke på att hela svepningen av theta på bilden är 180 grader kan du ungefär kontrollera att 3 stora toppar representerar 3 dominerande sluttningar på bilden.

Steg 4: Beräkna Rho Histogram

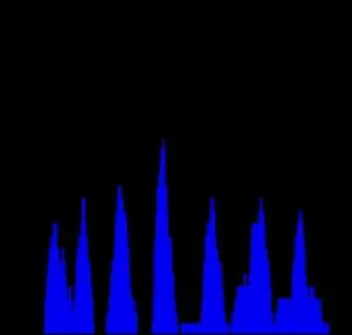
Nu när vi känner till tre huvudkluster av parallella linjer, låt oss separera linjer inom var och en av dem. Vi kan upprepa samma tillvägagångssätt. Låt oss ta en kolumn från Hough -utrymmet som motsvarar en topp på theta -histogrammet. Därefter kommer vi att beräkna ett annat histogram där X -axeln representerar rho -värde och Y - sammanfattade avläsningar för denna rho. Uppenbarligen blir summan mindre så det här diagrammet är inte så smidigt. Ändå är toppar tydligt synliga och antalet (7) motsvarar exakt antalet parallella linjer på källbilden. Tyvärr är inte alla diagrammen så perfekta, men principen är klar.

Steg 5: Hitta den centrala knuten

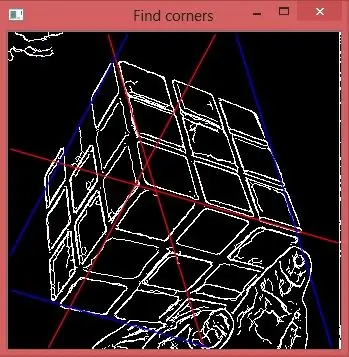
Om vi tar den centrala toppen på rho histogram för varje theta får vi 3 rader som är röda på bilden. Deras korsning markerar den nödvändiga punkten.

Steg 6: Välj mellan 2 alternativ

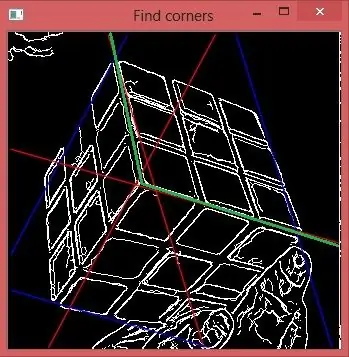
Du ser att varje linje går från den centrala punkten i båda riktningarna. Hur bestämmer man rätt halva? Låt oss ta theta3. Antag att vi tar den nedre delen av den här raden. Låt oss beräkna ännu ett Hough -utrymme endast för delen av bilden från 2 gröna linjer till det övre högra hörnet av bilden. Skapa sedan theta histogram för det. Du ser att den tredje toppen helt försvann så vi har gjort rätt val.

Steg 7: Bestäm de yttre hörnen

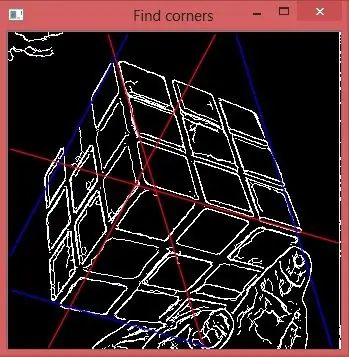
Nu kan vi använda den första och den sista toppen på rho -histogram för att rita blå linjer som skär de röda kanterna och markerar resten hörn. Uppgiften är löst.

Steg 8: Prova det i praktiken

Illustrationerna för denna instruerbara skapades med Perception 1.0. Detta är gratis programvara som använder OpenCV - ett kraftfullt bibliotek för datorsyn. Det kan också vara länkat till WinNB som användes i min andra Instructable och därmed ge visionskapacitet för robotik. Du kan ladda ner båda programmen från nbsite. För installation, kör bara den nedladdade exe -filen. Senare kan du ta bort det med standardverktyget i Windows. Webbplatsen innehåller också resurser om datorsyn och relaterade ämnen. I Perception hittar du den beskrivna metoden för 3D -rekonstruktion såväl som många andra. Fördelen med detta program är att det matar ut det slutliga resultatet tillsammans med mellanliggande data. Du kan undersöka hur datorsyn fungerar utan att vara programmerare. När det gäller inmatning har varje metod speciellt valt typiska prover. Naturligtvis kan du också använda din egen. Det är möjligt att mata in bilder från en fil eller från datorns kamera. Kontakta mig gärna med frågor eller förslag.