
Innehållsförteckning:
- Författare John Day day@howwhatproduce.com.
- Public 2024-01-30 12:36.
- Senast ändrad 2025-01-23 15:10.

Ett elektrokardiogram (EKG eller EKG) används för att mäta de elektriska signalerna som produceras av ett bankande hjärta och det spelar en stor roll vid diagnos och prognos av hjärt -kärlsjukdom. En del av informationen från ett EKG inkluderar rytmen i patientens hjärtslag och slagets styrka. Varje EKG -vågform genereras av en iteration av hjärtcykeln. Data samlas in genom en elektrod placerad på patientens hud. Signalen förstärks sedan och brus filtreras bort för att korrekt analysera data som finns. Genom att använda data som samlas in kan forskare inte bara diagnostisera hjärt -kärlsjukdomar, utan EKG har också spelat en stor roll för att öka förståelsen och erkännandet av mer oklara sjukdomar. Genomförandet av EKG har avsevärt förbättrat behandlingen av tillstånd som arytmi och ischemi [1].
Tillbehör:
Denna instruktion är för att simulera en virtuell EKG -enhet och därför är allt som krävs för att genomföra detta experiment en fungerande dator. Programvaran som används för följande simuleringar är LTspice XVII och kan laddas ner från internet.
Steg 1: Steg 1: Instrumentförstärkare




Den första komponenten i kretsen är en instrumentationsförstärkare. Som namnet antyder används instrumentförstärkaren för att öka signalens storlek. En EKG -signal som inte förstärks eller filtreras är ungefär 5 mV i amplitud. För att filtrera signalen måste den förstärkas. En rimlig förstärkning för denna krets måste vara stor för att den bioelektriska signalen ska filtreras på lämpligt sätt. Därför kommer förstärkningen för denna krets att vara cirka 1000. Den allmänna formen av en instrumentationsförstärkare ingår i bilderna för detta steg [2]. Förutom ekvationerna för kretsens förstärkning visas de värden som beräknades för varje komponent i den andra bilden [3].
Förstärkningen är negativ eftersom spänningen matas till inverteringsstiftet på operationsförstärkaren. Värdena som visas i den andra bilden hittades genom att ställa in värdena för R1, R2, R3 och förstärkning som önskade värden och sedan lösa för slutvärde R4. Den tredje bilden för detta steg är den simulerade kretsen i LTspice, komplett med exakta värden.
För att testa kretsen, både som helhet och som enskilda komponenter, bör en växelström (AC) -analys köras. Denna form av analys tittar på signalens storlek när frekvenserna ändras. Därför bör analystypen av AC-analyssvep vara ett decennium eftersom det ställer in skalan för x-axeln och är mer lämpligt för att exakt läsa resultaten. Per decennium bör det finnas 100 datapunkter. Detta kommer att exakt förmedla trenderna i data utan att överanstränga programmet, vilket garanterar effektivitet. Start- och stoppfrekvensvärdena bör omfatta båda avstängningsfrekvenserna. Därför är en rimlig startfrekvens 0,01 Hz och en rimlig stoppfrekvens är 1 kHz. För instrumentationsförstärkaren är ingångsfunktionen en sinusvåg med en magnitud på 5 mV. 5 mV motsvarar standardamplituden för en EKG -signal [4]. En sinusvåg härmar de förändrade aspekterna av en EKG -signal. Alla dessa analysinställningar, förutom ingångsspänningen, är desamma för varje komponent.
Den sista bilden är frekvensresponsdiagrammet för instrumentförstärkaren. Detta visar att instrumentationsförstärkaren kan öka insignalens storlek med cirka 1000. Den önskade förstärkningen för instrumentförstärkaren var 1000. Förstärkningen för den simulerade instrumentförstärkaren är 999,6, som hittas med hjälp av ekvationen som visas på det andra fotot. Procentfelet mellan den önskade förstärkningen och den experimentella förstärkningen är 0,04%. Detta är en acceptabel mängd felprocent.
Steg 2: Steg 2: Hakfilter




Nästa komponent som används i EKG -kretsen är ett aktivt filter. Ett aktivt filter är bara ett filter som kräver ström för att fungera. För denna uppgift är det bästa aktiva filtret som används ett hackfilter. Ett hackfilter används för att ta bort signal vid en enda frekvens eller ett mycket smalt frekvensområde. I denna krets är frekvensen som ska tas bort med ett hackfilter 60 Hz. 60 Hz är frekvensen som kraftledningar arbetar vid och är därför en stor bruskälla med enheter. Powerline -brus snedvrider biomedicinska signaler och sänker datakvaliteten [5]. Den allmänna formen av hackfilteret som används för denna krets visas i det första fotot för detta steg. Den aktiva komponenten i hackfilteret är bufferten som är ansluten. Bufferten används för att isolera signalen efter hackfilteret. Eftersom bufferten är en del av filtret och det behöver ström för att fungera, är hackfilteret den aktiva filterkomponenten i denna krets.
Ekvationen för resistiv- och kondensatorkomponenterna i hackfilteret visas på det andra fotot [6]. I ekvationen är fN frekvensen som ska tas bort, vilket är 60 Hz. Precis som instrumenteringsförstärkaren kan antingen motståndet eller kondensatorvärdet ställas in på valfritt värde och det andra värdet beräknas med ekvationen som visas i det andra fotot. För detta filter tilldelades C ett värde av 1 µF och resten av värdena hittades baserat på det värdet. Kondensatorns värde bestämdes utifrån bekvämlighet. Tabellen i det andra fotot visar värdena för 2R, R, 2C och C som användes.
Den tredje bilden för detta steg är den sista hackfilterkretsen med exakta värden. Med den kretsen kördes AC Sweep -analys med 5V. 5V motsvarar spänningen efter förstärkning. Resten av analysparametrarna är desamma som det som angavs i instrumentförstärkarsteget. Frekvensresponsdiagrammet visas i det sista fotot. Med hjälp av värdena och ekvationerna i det andra fotot är den faktiska frekvensen för hackfiltret 61,2 Hz. Det önskade värdet för hackfilteret var 60 Hz. Med hjälp av procentfelekvationen finns det ett 2% -fel mellan det simulerade filtret och det teoretiska filtret. Detta är en acceptabel mängd fel.
Steg 3: Steg 3: Lågpassfilter


Den sista typen av delar som används i denna krets är det passiva filtret. Som tidigare nämnts är ett passivt filter ett filter som inte kräver en strömkälla för att vara i drift. För ett EKG behövs både ett högpass och ett lågpassfilter för att korrekt avlägsna brus från signalen. Den första typen av passiva filter som ska läggas till kretsen är ett lågpassfilter. Som namnet antyder tillåter detta först att signalen under gränsfrekvensen passerar [7]. För lågpassfiltret bör avbrottsfrekvensen vara den övre gränsen för signalområdet. Som tidigare nämnts är EKG -signalens övre område 150 Hz [2]. Genom att sätta en övre gräns används inte brus från andra signaler vid signalinsamling.
Ekvationen för gränsfrekvensen är f = 1 / (2 * pi * R * C). Precis som med de tidigare kretskomponenterna kan värdena för R och C hittas genom att koppla in frekvensen och ställa in ett av komponentvärdena [7]. För lågpassfiltret inställdes kondensatorn på 1 µF och den önskade avstängningsfrekvensen är 150 Hz. Med hjälp av avstängningsfrekvensekvationen beräknas värdet för motståndskomponenten till 1 kΩ. Den första bilden för detta steg är en komplett lågpassfilter.
Samma parametrar definierade för hackfiltret används för AC Sweep Analysis av lågpassfiltret, som visas i den andra bilden. För denna komponent är den önskade avbrottsfrekvensen 150Hz och med ekvation 3 är den simulerade avstängningsfrekvensen 159 Hz. Detta har ett procentfel på 6%. Procentfelet för denna komponent är högre än föredraget men komponenterna valdes för enkel översättning till en fysisk krets. Detta är helt klart ett lågpassfilter, baserat på frekvensresponsdiagrammet i den andra bilden, eftersom endast signalen under gränsfrekvensen kan passera vid 5 V, och när frekvensen närmar sig avstängningsfrekvensen minskar spänningen.
Steg 4: Steg 4: Högpassfilter


Den andra passiva komponenten för EKG -kretsen är högpassfiltret. Ett högpassfilter är ett filter som tillåter att någon frekvens som är högre än gränsfrekvensen går igenom. För denna komponent är gränsfrekvensen 0,05 Hz. Återigen är 0,05 Hz den nedre änden av intervallet för EKG -signaler [2]. Även om värdet är så litet måste det fortfarande finnas ett högpassfilter för att filtrera bort eventuell spänningsförskjutning i signalen. Därför är högpassfiltret fortfarande nödvändigt inom kretsutformningen, även om avstängningsfrekvensen är så liten.
Ekvationen för gränsfrekvensen är densamma som lågpassningsfilteret, f = 1 / (2 * pi * R * C). Motståndsvärdet sattes till 50 kΩ och önskad avbrottsfrekvens är 0,05 Hz [8]. Med hjälp av denna information beräknades kondensatorns värde till 63 µF. Den första bilden för detta steg är högpassfiltret med lämpliga värden.
AC Sweep Analysis är det andra filtret. Liksom lågpassfiltret, när signalens frekvens närmar sig avstängningsfrekvensen, minskar utspänningen. För högpassfiltret är den önskade avstängningsfrekvensen 0,05 Hz och den simulerade avstängningsfrekvensen 0,0505 Hz. Detta värde beräknades med hjälp av lågpassfrekvensekvationen. Procentfelet för denna komponent är 1%. Detta är ett acceptabelt procentfel.
Steg 5: Steg 5: Full krets


Hela kretsen är konstruerad genom att ansluta de fyra komponenterna, instrumentationsförstärkaren, hackfilter, lågpassfilter och högpassfilter, i serie. Hela kretsschemat visas i den första bilden för detta steg.
Det simulerade svaret som visas i den andra figuren fungerar som det förväntades baseras på de typer av komponenter som används för denna krets. Kretsen som är designad filtrerar bort brus vid både de nedre och övre gränserna för EKG -signalen samt framgångsrikt filtrerar bort brus från kraftledningar. Lågpassfiltret tar bort signalen under avbrottsfrekvensen. Som visas i frekvensresponsdiagrammet, vid 0,01 Hz, passeras signalen vid 1 V, ett värde som är 5 gånger mindre än den önskade utsignalen. När frekvensen ökar ökar också utspänningen tills dess topp når 0,1 Hz. Toppen är cirka 5 V, vilket är i linje med en förstärkning på 1000 för instrumentförstärkaren. Signalen minskar från 5 V med början vid 10 Hz. När frekvensen är 60 Hz kommer det ingen signal som matas ut av kretsen. Detta var syftet med hackfilteret och det var avsett att motverka störningar hos kraftledningarna. Efter att frekvensen överstiger 60 Hz börjar spänningen igen öka med frekvensen. Slutligen, när frekvensen når 110 Hz når signalen som sekundär topp på ungefär 2 V. Därifrån minskar utsignalen på grund av lågpassfiltret.
Steg 6: Slutsats
Syftet med denna uppgift var att simulera ett automatiserat EKG som kan registrera hjärtcykeln exakt. För att göra detta behövde den analoga signalen som skulle ha tagits från en patient förstärkas och sedan filtreras för att endast inkludera EKG -signalen. Detta uppnåddes genom att först använda en instrumentationsförstärkare för att öka signalens storlek ungefär 1000 gånger. Då behövde bruset från kraftledningar avlägsnas från signalen samt brus ovanifrån och under det angivna frekvensområdet för ett EKG. Detta innebar att man införlivade ett aktivt hackfilter samt passiva hög- och lågpassfilter. Även om slutprodukten för denna uppgift var en simulerad krets, fanns det fortfarande ett acceptabelt fel, med hänsyn tagen till standardvärdena för resistiva och kapacitiva komponenter som normalt är tillgängliga. Över hela systemet fungerade som förväntat och skulle kunna överföras till en fysisk krets ganska enkelt.
Steg 7: Resurser
[1] X.-L. Yang, G.-Z. Liu, Y.-H. Tong, H. Yan, Z. Xu, Q. Chen, X. Liu, H.-H. Zhang, H.-B. Wang och S.-H. Tan, "Historien, hotspots och trender för elektrokardiogram", Journal of geriatric cardiology: JGC, juli 2015. [Uppkopplad]. Tillgänglig: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4554… [Åtkomst: 01-dec-2020].
[2] L. G. Tereshchenko och M. E. Josephson, "Frekvensinnehåll och egenskaper hos kammarledning," Journal of electrocardiology, 2015. [Online]. Tillgänglig: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4624… [Åtkomst: 01-dec-2020].
[3] "Differentialförstärkare-spänningsavdragaren", Grundläggande elektronikhandledning, 17-mar-2020. [Uppkopplad]. Tillgänglig: https://www.electronics-tutorials.ws/opamp/opamp_… [Åtkomst: 01-dec-2020].
[4] C.-H. Chen, S.-G. Pan och P. Kinget, "EKG -mätningssystem", Columbia University.
[5] S. Akwei-Sekyere, "Eliminering av kraftljudsbrus i biomedicinska signaler via blindkällseparation och wavelet-analys", PeerJ, 2-jul-2015. [Uppkopplad]. Tillgänglig: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4493… [Åtkomst: 01-dec-2020].
[6]”Bandstoppfilter kallas Avvisa filter”, Grundläggande elektronikstudier, 29 juni 2020. [Uppkopplad]. Tillgänglig: https://www.electronics-tutorials.ws/filter/band-… [Åtkomst: 01-dec-2020].
[7] “Lågpassfilter-Handledning för passivt RC-filter,” Grundläggande elektronikhandledning, 01-maj-2020. [Uppkopplad]. Tillgänglig: https://www.electronics-tutorials.ws/filter/filte… [Åtkomst: 01-dec-2020].
[8]”Högpassfilter-passivt RC-filterhandledning” Grundläggande elektronikhandledning, 05-mar-2019. [Uppkopplad]. Tillgänglig: https://www.electronics-tutorials.ws/filter/filter_3.html. [Åtkomst: 01-dec-2020].
Rekommenderad:
Automatiserat EKG: Amplifiering och filtersimuleringar med LTspice: 5 steg

Automatiserat EKG: förstärkning och filtersimuleringar med LTspice: Detta är bilden av den slutliga enheten som du ska bygga och en mycket ingående diskussion om varje del. Beskriver också beräkningarna för varje steg. Bilden visar blockdiagram för denna enhet Metoder och material: Syftet med denna pr
PHYS 339 Slutprojekt: Simple Theremin: 3 steg

PHYS 339 Final Project: Simple Theremin: Som fritidsmusiker och fysiker har jag alltid tyckt att theremins är det coolaste elektroniska instrumentet. Deras ljud är nästan hypnotiskt när det spelas av en professionell, och elektronikteorin som krävs för att de ska fungera är ganska
Bärbar - Slutprojekt: 7 steg
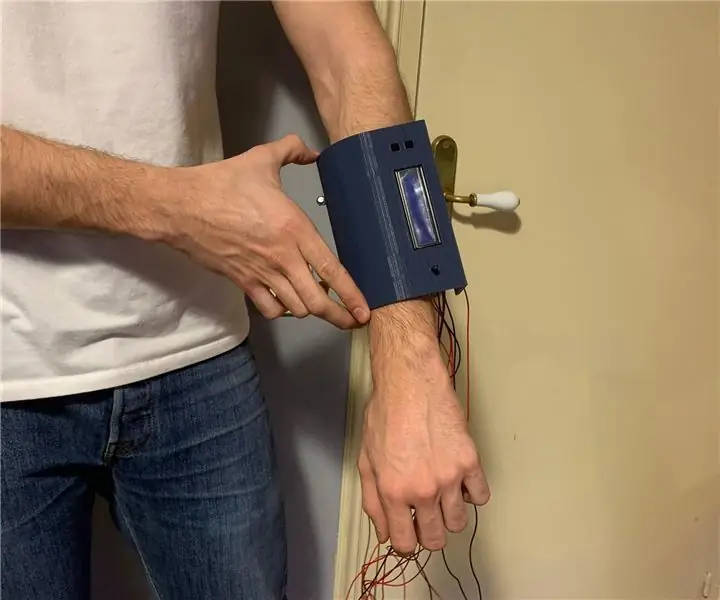
Bärbar - Slutprojekt: INLEDNING I detta projekt hade vi i uppgift att göra en funktionell bärbar prototyp baserad på en cyborg -funktioner. Visste du att ditt hjärta synkroniseras med BPM av musik? Du kan försöka kontrollera ditt humör genom musik, men tänk om vi låter
Enkelt automatiserat EKG (1 förstärkare, 2 filter): 7 steg

Lätt automatiserat EKG (1 förstärkare, 2 filter): Ett elektrokardiogram (EKG) mäter och visar hjärtats elektriska aktivitet med hjälp av olika elektroder placerade på huden. Ett EKG kan skapas med hjälp av en instrumentförstärkare, hackfilter och lågpassfilter. Slutligen filtrerade den
Slutprojekt LED Happy Face: 7 steg

Slutprojekt LED Happy Face: Välkommen till mitt happy face -projekt! This Instructable är ett något mer än nybörjare Arduino-projekt utformat för alla som bara vill ha kul med elektronik. Detta Arduino -projekt innebär att man använder 8 lysdioder som lyser från vänster till höger i
