Enkel Autorange kondensatortestare / kapacitansmätare med Arduino och för hand: 4 steg

2025 Författare: John Day | [email protected]. Senast ändrad: 2025-01-13 06:58

Hej!

För denna fysik-enhet behöver du:

* en strömförsörjning med 0-12V

* en eller flera kondensatorer

* ett eller flera laddningsmotstånd

* ett stoppur

* en multimeter för spänningsmätning

* en arduino nano

* en 16x2 I²C -skärm

* 1 / 4W motstånd med 220, 10k, 4.7M och 1Gohms 1 gohms motstånd

* duponttråd

Steg 1: Allmän information om kondensatorer

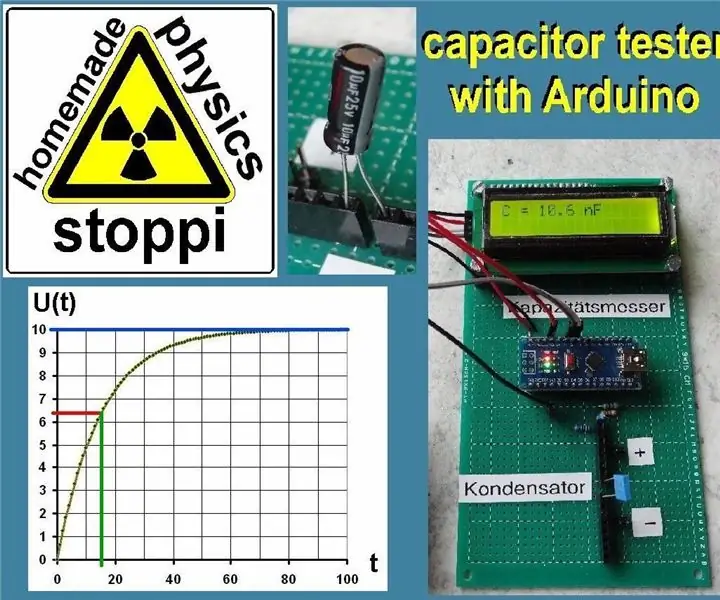
Kondensatorer spelar en mycket viktig roll inom elektronik. De används för att lagra avgifter, som ett filter, integrator etc. Men matematiskt finns det mycket i kondensatorer. Så du kan öva exponentiella funktioner med kondensatorer och de. träna. Om en initialt oladdad kondensator är ansluten via ett motstånd till en spänningskälla, flödar laddningarna kontinuerligt till kondensatorn. Med den ökande laddningen Q, enligt formeln Q = C * U (C = kondensatorns kapacitans), ökar också spänningen U över kondensatorn. Laddningsströmmen minskar dock mer och mer eftersom den snabbt laddade kondensatorn blir allt svårare att fylla med laddningar. Spänningen U (t) på kondensatorn följer följande formel:

U (t) = U0 * (1-exp (-k * t))

U0 är spänningen i strömförsörjningen, t är tiden och k är ett mått på laddningsprocessens hastighet. Vilka storlekar beror k på? Ju större lagringskapacitet (det vill säga kondensatorns kapacitans C), desto långsammare fylls den med laddningar och desto långsammare ökar spänningen. Ju större C, desto mindre k. Motståndet mellan kondensator och strömförsörjning begränsar också laddtransport. Ett större motstånd R orsakar en mindre ström I och därför flödar färre laddningar per sekund till kondensatorn. Ju större R, desto mindre k. Det rätta förhållandet mellan k och R eller C är:

k = 1 / (R * C).

Spänningen U (t) vid kondensatorn ökar således enligt formeln U (t) = U0 * (1-exp (-t / (R * C)))

Steg 2: Mätningarna

Eleverna ska ange spänningen U vid tidpunkten t i en tabell och sedan rita den exponentiella funktionen. Om spänningen ökar för snabbt måste du öka motståndet R. På andra sidan om spänningen ändras för långsamt, minska R.

Om man känner till U0, motståndet R och spänningen U (t) efter en viss tid t, kan kondensatorns kapacitans C beräknas utifrån detta. För detta måste man logaritma ekvationen och efter några transformationer får vi: C = -t / (R * ln (1 - U (t) / U0))

Exempel: U0 = 10V, R = 100 kohms, t = 7 sekunder, U (7 sek) = 3,54V. Då resulterar C i ett värde av C = 160 μF.

Men det finns en andra, enkel metod för att bestämma kapaciteten C. Spänningen U (t) efter t = R * C är nämligen exakt 63,2% av U0.

U (t) = U0 * (1-exp (-R * C / (R * C)) = U0 * (1-exp (-1)) = U0 * 0,632

Vad betyder det här? Eleverna måste bestämma tiden t efter vilken spänningen U (t) är exakt 63,2% av U0. Specifikt, för exemplet ovan, eftersträvas den tid då spänningen över kondensatorn är 10V * 0,632 = 6,3V. Detta är fallet efter 16 sekunder. Detta värde sätts nu in i ekvationen t = R * C: 16 = 100000 * C. Detta ger resultatet: C = 160 μF.

Steg 3: Arduino

I slutet av övningen kan kapaciteten också bestämmas med en Arduino. Detta beräknar kapaciteten C exakt enligt tidigare metod. Den laddar kondensatorn via ett känt motstånd R med 5V och bestämmer tiden efter vilken spänningen vid kondensatorn = 5V * 0,632 = 3,16V. För Arduino digital-till-analog-omvandlare är 5V lika med 1023. Därför är det bara att vänta tills värdet på den analoga ingången är 1023 * 3,16 / 5 = 647. Med denna tid kan kapaciteten C beräknas. Så att kondensatorer med mycket olika kapacitans kan mätas används 3 olika laddningsmotstånd. Först används ett lågt motstånd för att bestämma laddningstiden upp till 647. Om detta är för kort, dvs om kondensatorns kapacitans är för liten, väljs nästa högre laddningsmotstånd. Om detta också är för litet följer ett 1 Gohms -motstånd i slutet av mätningen. Värdet för C visas sedan på displayen med rätt enhet (µF, nF eller pF).

Steg 4: Slutsatser

Vad lär sig eleverna i denna enhet? Du kommer att lära dig om kondensatorer, deras kapacitans C, exponentiella funktioner, logaritm, procentberäkningar och Arduino. Jag tänker mycket.

Denna enhet är lämplig för studenter i åldern 16-17 år. Du måste redan ha gått igenom den exponentiella funktionen och logaritmen i matematik. Ha kul att testa det i din klass och Eureka!

Jag skulle bli väldigt glad om du skulle rösta på mig i klassrumstävlingen. Tack så mycket för detta!

Om du är intresserad av mina andra fysikprojekt, här är min youtube -kanal:

fler fysikprojekt: